16  Text Analysis 2

Keywords

text analysis, tidytext, tf-idf, topic modeling, ngrams, dtm, corpus, quanteda

16.1 Introduction

16.1.1 Learning Outcomes

• Expand strategies for analyzing text.
• Manipulate and analyze text data from a variety of sources using the {tidytext} package for …
  • Topic Modeling with TF-IDF Analysis.
  • Analysis of ngrams.
  • Converting to and from tidytext formats.

16.1.2 References:

• {ggraph} package Pedersen (2022)
• {igraph} package Csardi et al. (2023)
• {janeaustenr} package Silge (2023)
• {quanteda} package Benoit et al. (2018)
• {sentimentr} package Rinker (2018)
• Text Mining with R by Julia Silge and David Robinson Silge and Robinson (2022)
• {tidytext} package Silge and Robinson (2016)
• {tm} Text Mining Infrastructure package Feinerer and Hornik (2023)
• {topicmodels} package Grün and Hornik (2023)

16.1.2.1 Other References

• {matrix} package Bates, Maechler, and Jagan (2023)
• {tidytext} website Silge and Robinson (2023a)
• {tidytext} GitHub Silge and Robinson (2023b)
• {widyr} package Robinson and Silge (2022)
• {text2vec} package Selivanov (2023)
• {word2vec} package “Word2vec Package” (2023)

16.2 Topic Modeling

We have done frequency analysis to look at word usage and sentiment analysis to understand the emotional content of text.

Now the question is, what is the text really about?

• What is the topic or subject?
• What are key words or phrases most important to the text?
• How is a text similar or differnet from other texts?

One way is to compare a document with other documents is based on the relative rates of word usage across the documents.

• The other documents may be from a curated corpus, a general collection or group, or just a set of potentially similar works.

16.2.1 Term Frequency - Inverse Document Frequency (tf-idf)

Term Frequency is just how often a word (or term of multiple words) appears in a document (as we did before).

• Higher is more important - as long as it is meaningful, i.e., not a stop word.

Inverse Document Frequency is a function that scores the frequency of word usage across multiple documents.

• A word’s score (importance) decreases if it is used across multiple documents - it’s more common.
• A word’s score (importance) increases if it is not used across multiple documents - it’s more specific to a document.

We multiply \(tf\) by \(idf\) to calculate the \(tf-idf\) for a term in a single document as part of a collection of documents, as shown in Table 16.1.

Table 16.1: Elements in tf-idf

Term Frequency (for a term in one document)	\(tf\)	\(\frac{n_{\text{term}}}{n_{\text{total words in the document}}}\)
Inverse Document Frequency (for a term across documents):	\(idf\)	\(\text{ln}\left(\frac{n_{\text{documents}}}{n_{\text{documents containing term}}}\right)\)
\(tf-idf\) (for a term in one document of out multiple documents)	\(tf\)-\(idf\)	\(tf \times idf\)

Important

The tf-idf is a heuristic measure of the relative importance of a term to a single document out of a collection of documents

• These are the base formulas and they (or some extensions) are used in multiple NLP processes.

16.2.1.1 TF in Jane Austen’s Novels

Load the {tidyverse}, {tidytext}, and {janeaustenr} packages.

library(tidyverse)
library(tidytext)
library(janeaustenr)

Count the total words and most commonly used words across the books.

• Do not eliminate the stop words!
• We want all the words to get the correct relative frequencies.

austen_books() |>
  unnest_tokens(word, text) |>
  mutate(word = str_extract(word, "[a-z']+")) |>
  count(book, word, sort = TRUE) ->
book_words

book_words |>
  group_by(book) |>
  summarize(total = sum(n), .groups = "drop") ->
total_words

book_words |>
  left_join(total_words, by = "book") ->
book_words

book_words

# A tibble: 39,708 × 4
   book              word      n  total
   <fct>             <chr> <int>  <int>
 1 Mansfield Park    the    6209 160460
 2 Mansfield Park    to     5477 160460
 3 Mansfield Park    and    5439 160460
 4 Emma              to     5242 160996
 5 Emma              the    5204 160996
 6 Emma              and    4897 160996
 7 Mansfield Park    of     4778 160460
 8 Pride & Prejudice the    4331 122204
 9 Emma              of     4293 160996
10 Pride & Prejudice to     4163 122204
# ℹ 39,698 more rows

• Plot the tf for each book (should look familiar).

book_words |>
  ggplot(aes(n / total, fill = book)) +
  geom_histogram(show.legend = FALSE) +
  xlim(NA, 0.0009) +
  facet_wrap(~book, ncol = 2, scales = "free_y")

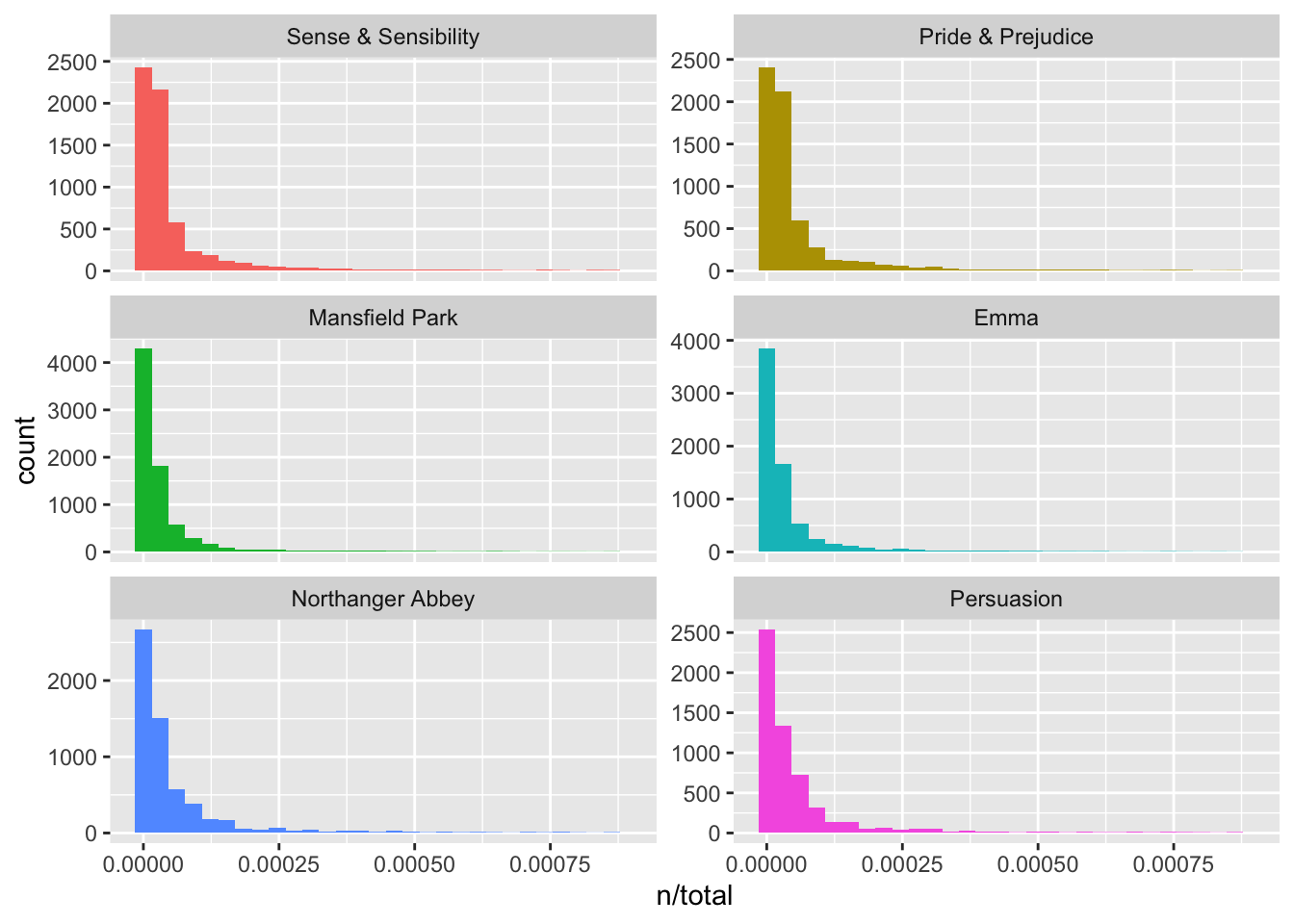
• There are numerous words that only occur once in each book.

book_words |>
  filter(n == 1) |>
  nrow()

[1] 15929

16.2.1.2 Background on Zipf’s Law

The long-tailed distributions we just saw are common in language and are well-studied.

Zipf’s law, named after George Zipf, a 20^th century American linguist states:

• The frequency of word is inversely proportional to its rank.
  • Frequency is how often a word is used, and,
  • Rank is the position of the word from the top of a list of the words sorted in descending order by their frequencies.
• Example: the most frequently used word (rank = 1) might have frequency .05% and the rank 5 word might have frequency=.01% and so on.
• Note, we are NOT removing stop words in these analyses as that would affect the distributions.

16.2.1.3 Zipf’s law for Jane Austen

Let’s look at how this applies in Jane Austen’s works.

book_words |>
  group_by(book) |>
  mutate(
    rank = row_number(),
    term_frequency = n / total
  ) ->
freq_by_rank

head(freq_by_rank, 10)

# A tibble: 10 × 6
# Groups:   book [3]
   book              word      n  total  rank term_frequency
   <fct>             <chr> <int>  <int> <int>          <dbl>
 1 Mansfield Park    the    6209 160460     1         0.0387
 2 Mansfield Park    to     5477 160460     2         0.0341
 3 Mansfield Park    and    5439 160460     3         0.0339
 4 Emma              to     5242 160996     1         0.0326
 5 Emma              the    5204 160996     2         0.0323
 6 Emma              and    4897 160996     3         0.0304
 7 Mansfield Park    of     4778 160460     4         0.0298
 8 Pride & Prejudice the    4331 122204     1         0.0354
 9 Emma              of     4293 160996     4         0.0267
10 Pride & Prejudice to     4163 122204     2         0.0341

Zipf’s law is often visualized by plotting rank on the x-axis and term frequency on the y-axis, on logarithmic scales.

• Plotting this way, an inversely proportional relationship will have a constant, negative slope.

freq_by_rank |>
  ggplot(aes(rank, term_frequency, color = book)) +
  geom_line(size = 1.1, alpha = 0.8, show.legend = FALSE) +
  scale_x_log10() +
  scale_y_log10()

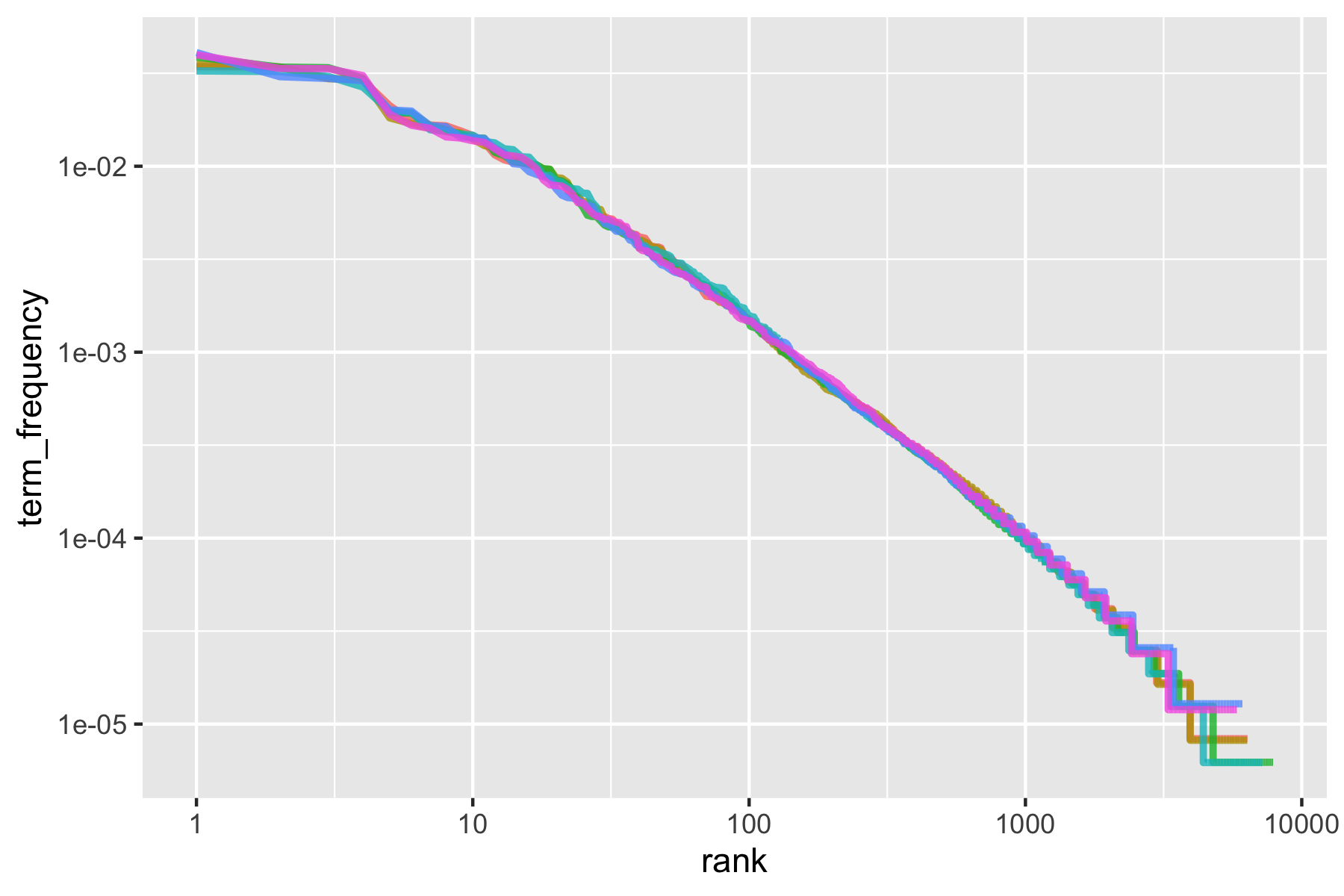
We can see the pattern is quite similar for all six novels - a negative slope.

• It’s not quite linear though.

Let’s try to model the middle segment, between ranks 10 and 500, as linear.

freq_by_rank |>
  filter(rank < 500, rank > 10) ->
rank_subset

lmout <- lm(log10(term_frequency) ~ log10(rank), data = rank_subset)
broom::tidy(lmout)[c(1, 2, 5)]

# A tibble: 2 × 3
  term        estimate p.value
  <chr>          <dbl>   <dbl>
1 (Intercept)   -0.621       0
2 log10(rank)   -1.11        0

Classic versions of Zipf’s law have \(\text{frequency} \propto \frac{1}{\text{rank}}\).

• Our model has a slope close to -1.
• Let’s plot this fitted line.

freq_by_rank |>
  ggplot(aes(rank, term_frequency, color = book)) +
  geom_abline(
    intercept = -0.62, slope = -1.1,
    color = "red", linetype = 2
  ) +
  geom_line(size = 1.1, alpha = 0.8, show.legend = FALSE) +
  scale_x_log10() +
  scale_y_log10()

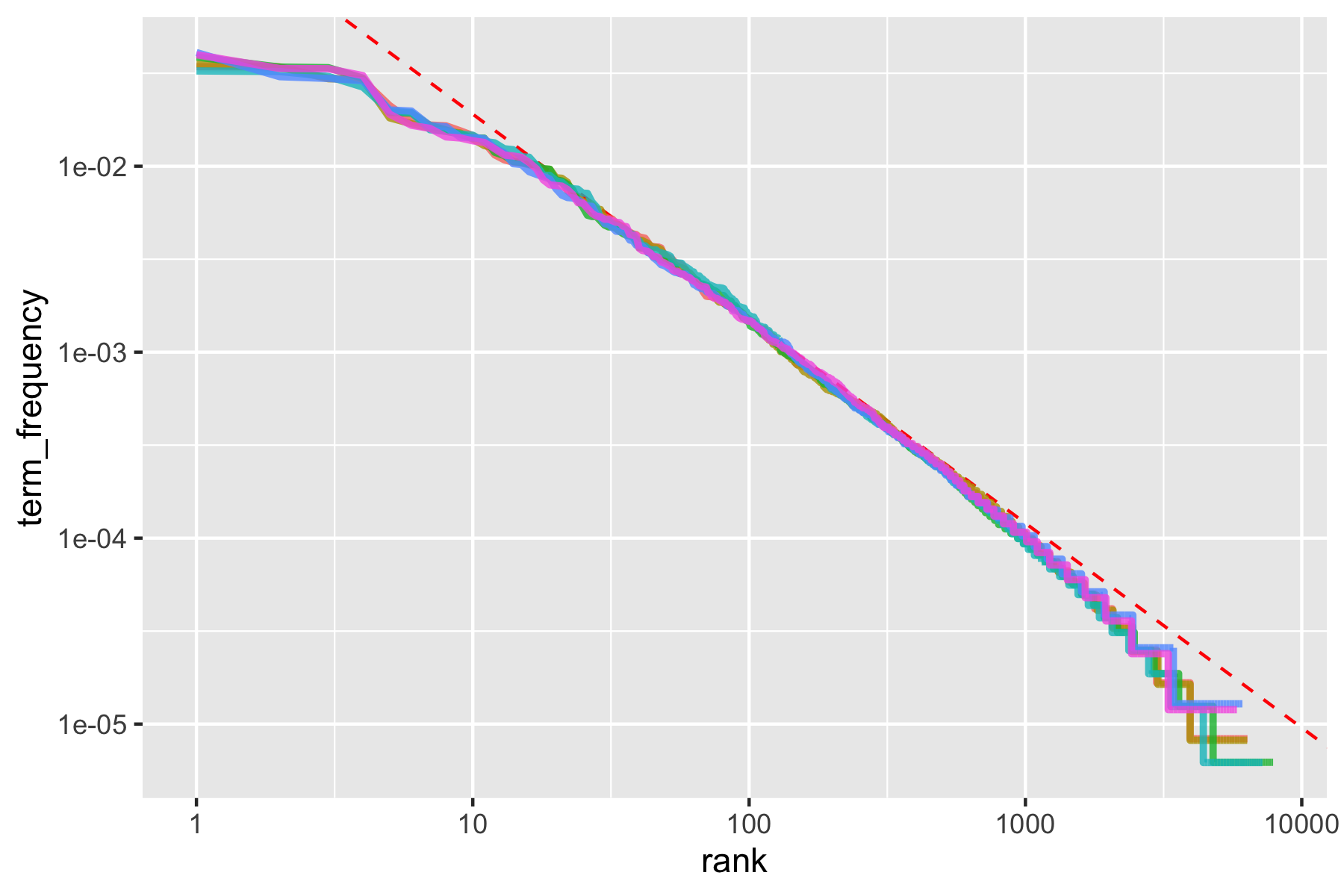
• The result is close to the classic version of Zipf’s law for the corpus of Jane Austen’s novels.
  • The deviations at high rank (> 1000) are not uncommon for many kinds of language; a corpus of language often contains fewer rare words than predicted by a single power law.
  • The deviations at low rank (<10) are more unusual. Jane Austen uses a lower percentage of the most common words than many collections of language.

This kind of analysis could be extended to compare authors, or to compare any other collections of text; it can be implemented simply using tidy data principles.

• There is a whole field to determining authorship through analysis of an author’s style called Stylometry. See Introduction to stylometry with Python for a nice introduction in Python.

16.2.2 Analyzing A Corpus with tf-idf

The bind_tf_idf() function calculates the tf-idf for us.

The idea for \(tf-idf\) is to find the words important to a specific document by

• decreasing the weight (value) for words commonly used in a collection of other documents, and,
• increasing the weight for words not used very much in a collection of other documents, (e.g., Jane Austen’s novels).

Calculating tf-idf attempts to find the words that are important (i.e., common) in a document, but not too common across documents.

Let’s use bind_tf_idf() on a tidytext-formatted tibble (one row per term (token), per document).

• It returns a tibble with new columns tf, idf, and tf-idf.

book_words |>
  bind_tf_idf(word, book, n) ->
book_words

arrange(book_words, tf_idf, word) |> head(10)

# A tibble: 10 × 7
   book                word          n  total        tf   idf tf_idf
   <fct>               <chr>     <int>  <int>     <dbl> <dbl>  <dbl>
 1 Emma                a          3130 160996 0.0194        0      0
 2 Mansfield Park      a          3100 160460 0.0193        0      0
 3 Sense & Sensibility a          2092 119957 0.0174        0      0
 4 Pride & Prejudice   a          1954 122204 0.0160        0      0
 5 Persuasion          a          1594  83658 0.0191        0      0
 6 Northanger Abbey    a          1540  77780 0.0198        0      0
 7 Sense & Sensibility abilities     9 119957 0.0000750     0      0
 8 Pride & Prejudice   abilities     6 122204 0.0000491     0      0
 9 Mansfield Park      abilities     5 160460 0.0000312     0      0
10 Emma                abilities     3 160996 0.0000186     0      0

The \(idf\), and thus \(tf-idf\), are zero for extremely common words.

• If they appear in all six novels, the \(idf\) term is \(log(1) = 0\).

In general, the \(idf\) (and thus \(tf-idf\)) is very low (near zero) for words that occur in many of the documents in a collection; this is how this approach decreases the weight for common words.

• The \(idf\) will be higher for words that occur in fewer documents.

Let’s look at terms with high \(tf-idf\) in Jane Austen’s works.

book_words |>
  select(-total) |>
  arrange(desc(tf_idf)) |>
  head(10)

# A tibble: 10 × 6
   book                word          n      tf   idf  tf_idf
   <fct>               <chr>     <int>   <dbl> <dbl>   <dbl>
 1 Sense & Sensibility elinor      623 0.00519  1.79 0.00931
 2 Sense & Sensibility marianne    492 0.00410  1.79 0.00735
 3 Mansfield Park      crawford    493 0.00307  1.79 0.00551
 4 Pride & Prejudice   darcy       374 0.00306  1.79 0.00548
 5 Persuasion          elliot      254 0.00304  1.79 0.00544
 6 Emma                emma        786 0.00488  1.10 0.00536
 7 Northanger Abbey    tilney      196 0.00252  1.79 0.00452
 8 Emma                weston      389 0.00242  1.79 0.00433
 9 Pride & Prejudice   bennet      294 0.00241  1.79 0.00431
10 Persuasion          wentworth   191 0.00228  1.79 0.00409

As we saw before, the names of people and places tend to be important in each novel.

• None of these occur in all of the novels and are primarily in one or two of them.

We can plot these.

book_words |>
  arrange(desc(tf_idf)) |>
  mutate(word = fct_rev(parse_factor(word))) |> ## ordering for ggplot
  group_by(book) |>
  slice_max(order_by = tf_idf, n = 10) |>
  ungroup() |>
  ggplot(aes(word, tf_idf, fill = book)) +
  geom_col(show.legend = FALSE) +
  labs(x = NULL, y = "tf-idf") +
  facet_wrap(~book, ncol = 2, scales = "free") +
  coord_flip()

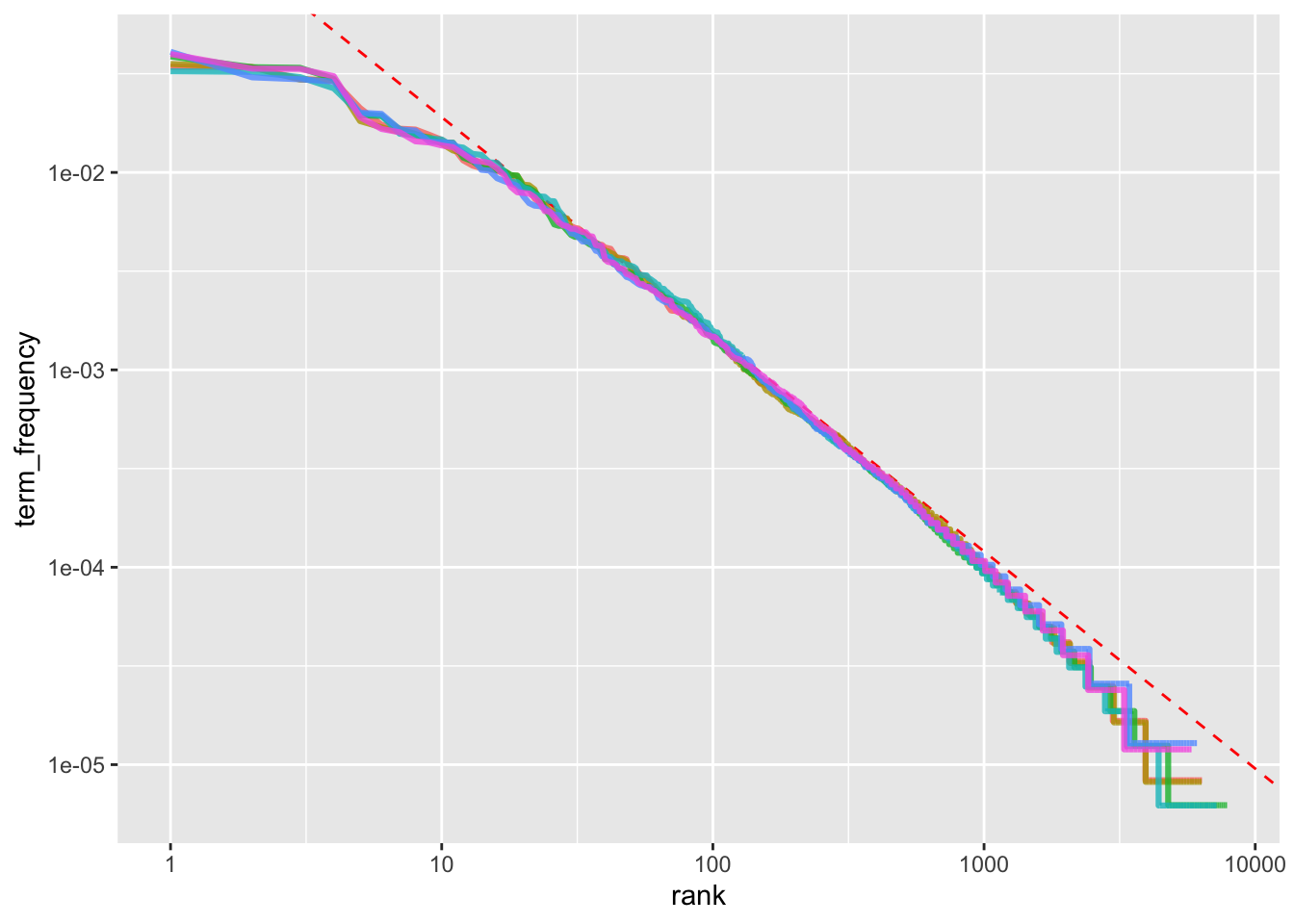
Measuring \(tf-idf\) shows Jane Austen used similar language across her six novels, and what distinguishes one novel from the rest are the proper nouns.

This is the point of \(tf-idf\); it identifies words important to one document within a collection of documents.

16.2.2.1 Example: Using tf-idf to Analyze a Corpus of Physics Texts

Let’s download the following the following (translated) documents dealing with different ideas in science:

• Discourse on Floating Bodies by Galileo Galilei, born 1564,
• Treatise on Light by Christiaan Huygens, born 1629,
  
• Experiments with Alternate Currents of High Potential and High Frequency by Nikola Tesla born 1856, and
• Relativity: The Special and General Theory by Albert Einstein, born 1879.
• The gutenberg ids are: 37729, 14725, 13476, and 30155.

Let’s include the authors as part of the meta-data we can select when we download them so we can download all at once.

Before we can use bind_tf_idf(), we have to unnest the terms, get rid of the formatting, and get the counts as before.

library(gutenbergr)
physics <- gutenberg_download(c(37729, 14725, 13476, 30155),
  meta_fields = "author"
)
physics |>
  unnest_tokens(word, text) |>
  mutate(word = str_extract(word, "[a-z']+")) |>
  count(author, word, sort = TRUE) ->
physics_words

physics_words |>
  head(10)

# A tibble: 10 × 3
   author              word      n
   <chr>               <chr> <int>
 1 Galilei, Galileo    the    3770
 2 Tesla, Nikola       the    3606
 3 Huygens, Christiaan the    3553
 4 Einstein, Albert    the    2995
 5 Galilei, Galileo    of     2051
 6 Einstein, Albert    of     2029
 7 Tesla, Nikola       of     1737
 8 Huygens, Christiaan of     1708
 9 Huygens, Christiaan to     1207
10 Tesla, Nikola       a      1176

We can now use bind_tf-idf() (which helps normalize across the documents of different lengths).

physics_words |>
  bind_tf_idf(word, author, n) |>
  mutate(word = fct_reorder(word, tf_idf)) |>
  mutate(author = factor(author, levels = c(
    "Galilei, Galileo",
    "Huygens, Christiaan",
    "Tesla, Nikola",
    "Einstein, Albert"
  ))) ->
physics_plot

Let’s plot the words by \(tf-idf\).

physics_plot |>
  group_by(author) |>
  slice_max(order_by = tf_idf, n = 15) |>
  ungroup() |>
  mutate(word = fct_reorder(word, tf_idf)) |>
  ggplot(aes(word, tf_idf, fill = author)) +
  geom_col(show.legend = FALSE) +
  labs(x = NULL, y = "tf-idf") +
  facet_wrap(~author, ncol = 2, scales = "free") +
  coord_flip()

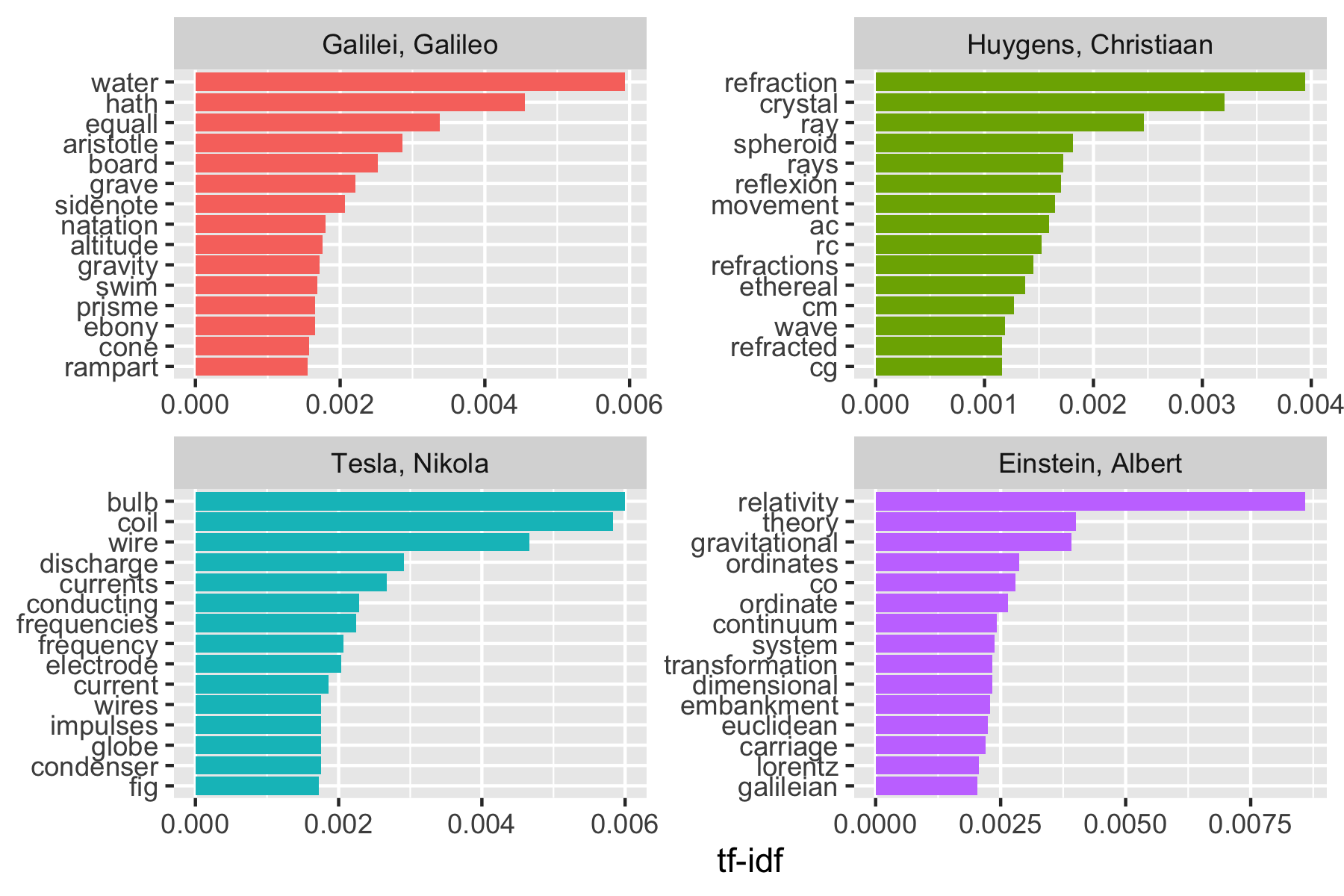
Note we have some unusual words due to how tidytext separates words by hyphens

• We could get rid of them early in the process
• We also have what appear to be abbreviations: RC, AC, CM, fig, cg, …

physics |>
  filter(str_detect(text, "RC")) |>
  select(text)

# A tibble: 44 × 1
   text                                                                  
   <chr>                                                                 
 1 line RC, parallel and equal to AB, to be a portion of a wave of light,
 2 represents the partial wave coming from the point A, after the wave RC
 3 be the propagation of the wave RC which fell on AB, and would be the  
 4 transparent body; seeing that the wave RC, having come to the aperture
 5 incident rays. Let there be such a ray RC falling upon the surface    
 6 CK. Make CO perpendicular to RC, and across the angle KCO adjust OK,  
 7 the required refraction of the ray RC. The demonstration of this is,  
 8 explaining ordinary refraction. For the refraction of the ray RC is   
 9 29. Now as we have found CI the refraction of the ray RC, similarly   
10 the ray _r_C is inclined equally with RC, the line C_d_ will          
# ℹ 34 more rows

We can remove these by creating our own custom stop words tibble and doing an anti-join.

mystopwords <- tibble(word = c(
  "eq", "co", "rc", "ac", "ak", "bn",
  "fig", "file", "cg", "cb", "cm",
  "ab"
))

physics_words <- anti_join(physics_words, mystopwords,
  by = "word"
)

plot_physics <- physics_words |>
  bind_tf_idf(word, author, n) |>
  mutate(word = str_remove_all(word, "_")) |>
  group_by(author) |>
  slice_max(order_by = tf_idf, n = 15) |>
  ungroup() |>
  mutate(word = reorder_within(word, tf_idf, author)) |>
  mutate(author = factor(author, levels = c(
    "Galilei, Galileo",
    "Huygens, Christiaan",
    "Tesla, Nikola",
    "Einstein, Albert"
  )))

ggplot(plot_physics, aes(word, tf_idf, fill = author)) +
  geom_col(show.legend = FALSE) +
  labs(x = NULL, y = "tf-idf") +
  facet_wrap(~author, ncol = 2, scales = "free") +
  coord_flip() +
  scale_x_reordered()

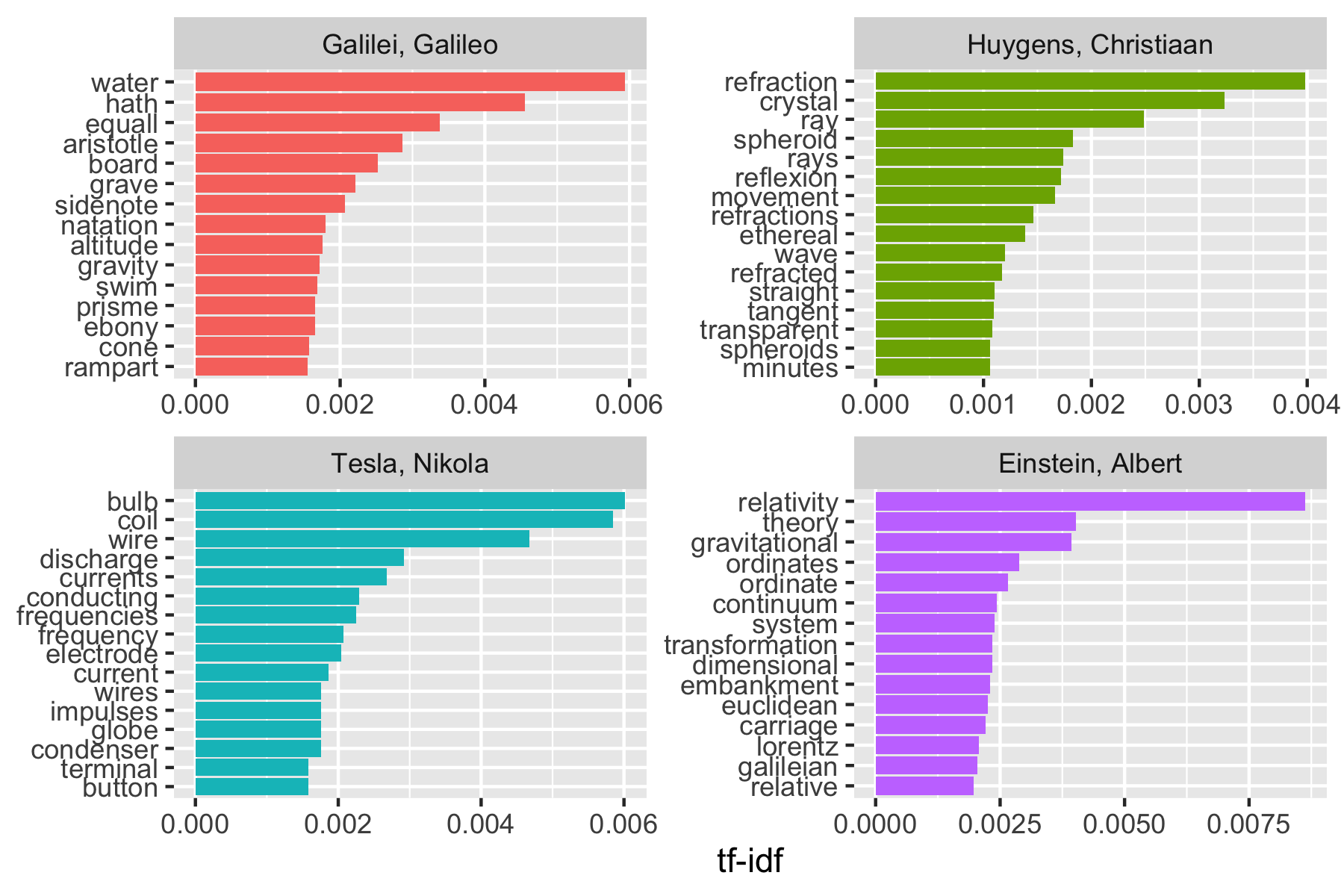
You could do even more cleaning using regex and repeating if desired,

Even at this level, it’s pretty clear the four books have something to do with water, light, electricity and gravity (yes, we could also read the titles).

16.2.3 Topic Modeling Summary

The tf-idf approach allows us to find words that are characteristic for one document within a corpus or collection of documents, whether that document is a novel, a physics text, or a webpage.

16.3 Relationships Between Words: Analyzing n-Grams

We’ve analyzed words as individual units (within blocks of text of various sizes), and considered their relationships to sentiments or to documents.

We will now look at text analyses based on the relationships between groups of words, examining which words tend to follow others immediately, or, that tend to co-occur within the same documents.

16.3.1 Tokenizing by n-gram

We can use the function unnest_tokens() to create consecutive sequences of words, called n-grams.

• By seeing how often word X is followed by word Y, we can build a model of the relationship between the two words.
• We add the argument token = "ngrams" to unnest_tokens(), with the argument n = the number of words we wish to capture in each n-gram.
  • n = 2 creates pairs of two consecutive words, often called a “bigram”.

Austen Books example.

austen_books() |>
  unnest_tokens(bigram, text, token = "ngrams", n = 2) ->
austen_bigrams
austen_bigrams

# A tibble: 675,025 × 2
   book                bigram         
   <fct>               <chr>          
 1 Sense & Sensibility sense and      
 2 Sense & Sensibility and sensibility
 3 Sense & Sensibility <NA>           
 4 Sense & Sensibility by jane        
 5 Sense & Sensibility jane austen    
 6 Sense & Sensibility <NA>           
 7 Sense & Sensibility <NA>           
 8 Sense & Sensibility <NA>           
 9 Sense & Sensibility <NA>           
10 Sense & Sensibility <NA>           
# ℹ 675,015 more rows

• These bigrams overlap: “sense and” is one token, while “and sensibility” is another.

16.3.2 Counting and filtering n-Grams

Our usual tidy tools apply equally well to n-gram analysis.

austen_bigrams |>
  count(bigram, sort = TRUE)

# A tibble: 193,210 × 2
   bigram      n
   <chr>   <int>
 1 <NA>    12242
 2 of the   2853
 3 to be    2670
 4 in the   2221
 5 it was   1691
 6 i am     1485
 7 she had  1405
 8 of her   1363
 9 to the   1315
10 she was  1309
# ℹ 193,200 more rows

As you might expect, a lot of the most common bigrams are pairs of common (uninteresting) words.

We can get rid of these by using separate_wider_delim() and then removing rows where either word is a stop word.

austen_bigrams |>
  separate_wider_delim(bigram, names = c("word1", "word2"), delim = " ") ->
bigrams_separated

bigrams_separated |>
  filter(!word1 %in% stop_words$word) |>
  filter(!word2 %in% stop_words$word) ->
bigrams_filtered

## new bigram counts:
bigrams_filtered |>
  count(word1, word2, sort = TRUE) ->
bigram_counts

bigram_counts

# A tibble: 28,975 × 3
   word1   word2         n
   <chr>   <chr>     <int>
 1 <NA>    <NA>      12242
 2 sir     thomas      266
 3 miss    crawford    196
 4 captain wentworth   143
 5 miss    woodhouse   143
 6 frank   churchill   114
 7 lady    russell     110
 8 sir     walter      108
 9 lady    bertram     101
10 miss    fairfax      98
# ℹ 28,965 more rows

We can now unite() them back together.

bigrams_filtered |>
  unite(bigram, word1, word2, sep = " ") ->
bigrams_united

bigrams_united |>
  count(bigram, sort = TRUE)

# A tibble: 28,975 × 2
   bigram                n
   <chr>             <int>
 1 NA NA             12242
 2 sir thomas          266
 3 miss crawford       196
 4 captain wentworth   143
 5 miss woodhouse      143
 6 frank churchill     114
 7 lady russell        110
 8 sir walter          108
 9 lady bertram        101
10 miss fairfax         98
# ℹ 28,965 more rows

16.3.3 Analyzing bigrams

This one-bigram-per-row format is helpful for exploratory analyses of the text.

As a simple example, what are the most common “streets” mentioned in each book?

bigrams_filtered |>
  filter(word2 == "street") |>
  count(book, word1, sort = TRUE)

# A tibble: 33 × 3
   book                word1           n
   <fct>               <chr>       <int>
 1 Sense & Sensibility harley         16
 2 Sense & Sensibility berkeley       15
 3 Northanger Abbey    milsom         10
 4 Northanger Abbey    pulteney       10
 5 Mansfield Park      wimpole         9
 6 Pride & Prejudice   gracechurch     8
 7 Persuasion          milsom          5
 8 Sense & Sensibility bond            4
 9 Sense & Sensibility conduit         4
10 Persuasion          rivers          4
# ℹ 23 more rows

# or
bigrams_united |>
  filter(str_detect(bigram, "street")) |>
  count(book, bigram, sort = TRUE)

# A tibble: 51 × 3
   book                bigram                 n
   <fct>               <chr>              <int>
 1 Sense & Sensibility harley street         16
 2 Sense & Sensibility berkeley street       15
 3 Northanger Abbey    milsom street         10
 4 Northanger Abbey    pulteney street       10
 5 Mansfield Park      wimpole street         9
 6 Pride & Prejudice   gracechurch street     8
 7 Persuasion          milsom street          5
 8 Sense & Sensibility bond street            4
 9 Sense & Sensibility conduit street         4
10 Persuasion          rivers street          4
# ℹ 41 more rows

A bigram can also be treated as a “term” in a document in the same way we treated individual words.

We can calculate the \(tf-idf\) of bigrams.

bigrams_united |>
  count(book, bigram) |>
  bind_tf_idf(bigram, book, n) |>
  arrange(desc(tf_idf)) ->
bigram_tf_idf

bigram_tf_idf

# A tibble: 31,397 × 6
   book                bigram                n     tf   idf tf_idf
   <fct>               <chr>             <int>  <dbl> <dbl>  <dbl>
 1 Mansfield Park      sir thomas          266 0.0244  1.79 0.0438
 2 Persuasion          captain wentworth   143 0.0232  1.79 0.0416
 3 Mansfield Park      miss crawford       196 0.0180  1.79 0.0322
 4 Persuasion          lady russell        110 0.0179  1.79 0.0320
 5 Persuasion          sir walter          108 0.0175  1.79 0.0314
 6 Emma                miss woodhouse      143 0.0129  1.79 0.0231
 7 Northanger Abbey    miss tilney          74 0.0128  1.79 0.0229
 8 Sense & Sensibility colonel brandon      96 0.0115  1.79 0.0205
 9 Sense & Sensibility sir john             94 0.0112  1.79 0.0201
10 Emma                frank churchill     114 0.0103  1.79 0.0184
# ℹ 31,387 more rows

And plot as well.

bigram_tf_idf |>
  group_by(book) |>
  slice_max(order_by = tf_idf, n = 10) |>
  ungroup() |>
  mutate(bigram = reorder_within(bigram, tf_idf, book)) |>
  ggplot(aes(bigram, tf_idf, fill = book)) +
  geom_col(show.legend = FALSE) +
  labs(x = NULL, y = "tf-idf") +
  facet_wrap(~book, ncol = 2, scales = "free") +
  coord_flip() +
  scale_x_reordered()

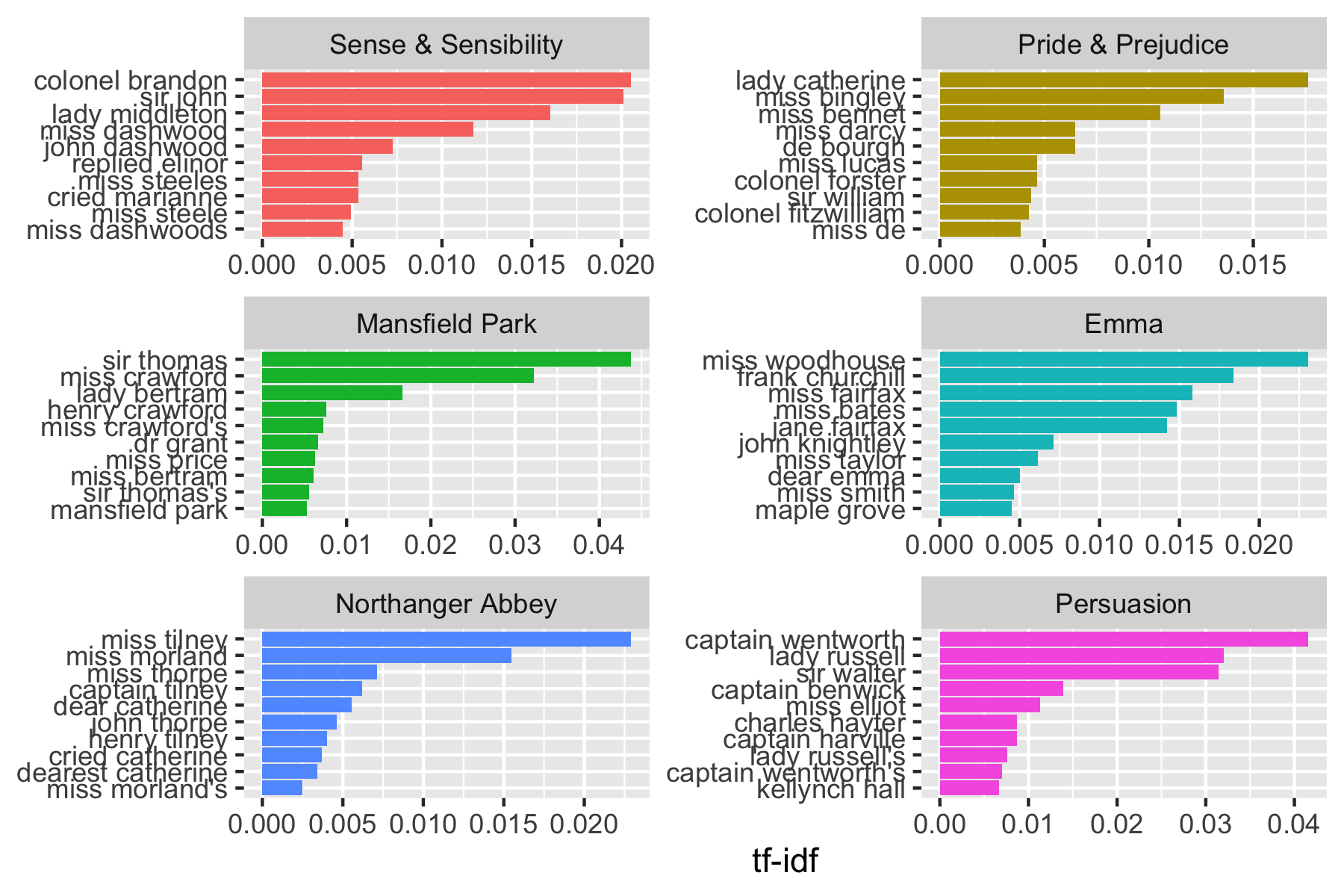
16.3.4 Bigrams in Sentiment Analysis

Per the Readme to the {Sentimentr} package:

• English (and other languages) uses Valence Shifters: words that modify the sentiment of other words. Examples include:

  • A negator: flips the sign of a polarized word (e.g., “I do not like it.”).
  • An amplifier or intensifier increases the impact of a polarized word (e.g., “I really like it.”).
  • A de-amplifier or diminisher (downtoner) reduces the impact of a polarized word (e.g., “I hardly like it.”).
    
  • An adversative conjunction overrules the previous clause containing a polarized word (e.g., “I like it but it’s not worth it.”).

These are fairly common in normal usage:

• Negators can appear in 20% of sentences with a polarized word.
• Adversative conjunctions can appear 10% of the time.
• Also see Sentiment Classification of Movie Reviews Using Contextual Valence Shifters

When analyzing at the word level or even sentences, the analysis tends to miss the action of valence shifters.

• At a minimum, a negation cancels out a sentiment word so the sentence (or text block) is neutral as opposed to its true, shifted sentiment.

A small step towards improving analysis of sentiment is looking at how often words are preceded by the word “not” on the bigrams.

bigrams_separated |>
  filter(word1 == "not") |>
  count(word1, word2, sort = TRUE)

# A tibble: 1,178 × 3
   word1 word2     n
   <chr> <chr> <int>
 1 not   be      580
 2 not   to      335
 3 not   have    307
 4 not   know    237
 5 not   a       184
 6 not   think   162
 7 not   been    151
 8 not   the     135
 9 not   at      126
10 not   in      110
# ℹ 1,168 more rows

Performing sentiment analysis on the bigram data examines how often sentiment-associated words are preceded by “not” or other negating words.

• We could use this to ignore or even reverse their contribution to the sentiment score.

Example: Let’s use the AFINN lexicon (has numeric sentiment values, positive or negative).

library(textdata)
AFINN <- get_sentiments("afinn")
AFINN

# A tibble: 2,477 × 2
   word       value
   <chr>      <dbl>
 1 abandon       -2
 2 abandoned     -2
 3 abandons      -2
 4 abducted      -2
 5 abduction     -2
 6 abductions    -2
 7 abhor         -3
 8 abhorred      -3
 9 abhorrent     -3
10 abhors        -3
# ℹ 2,467 more rows

Find the most frequent words preceded by “not” and associated with a sentiment.

bigrams_separated |>
  filter(word1 == "not") |>
  inner_join(AFINN, by = c(word2 = "word")) |>
  count(word2, value, sort = TRUE) ->
not_words

not_words

# A tibble: 229 × 3
   word2   value     n
   <chr>   <dbl> <int>
 1 like        2    95
 2 help        2    77
 3 want        1    41
 4 wish        1    39
 5 allow       1    30
 6 care        2    21
 7 sorry      -1    20
 8 leave      -1    17
 9 pretend    -1    17
10 worth       2    17
# ℹ 219 more rows

Which words contributed the most in the “wrong” direction?

Let’s multiply their value by the number of times they appear (so a word with a value of +3 occurring 10 times has as much impact as a word with a value of +1 occurring 30 times).

Visualize the result with a bar plot.

not_words |>
  mutate(contribution = n * value) |>
  arrange(desc(abs(contribution))) |>
  head(20) |>
  mutate(word2 = reorder(word2, contribution)) |>
  ggplot(aes(word2, n * value, fill = n * value > 0)) +
  geom_col(show.legend = FALSE) +
  xlab("Words preceded by \"not\"") +
  ylab("Sentiment value * number of occurrences") +
  coord_flip()

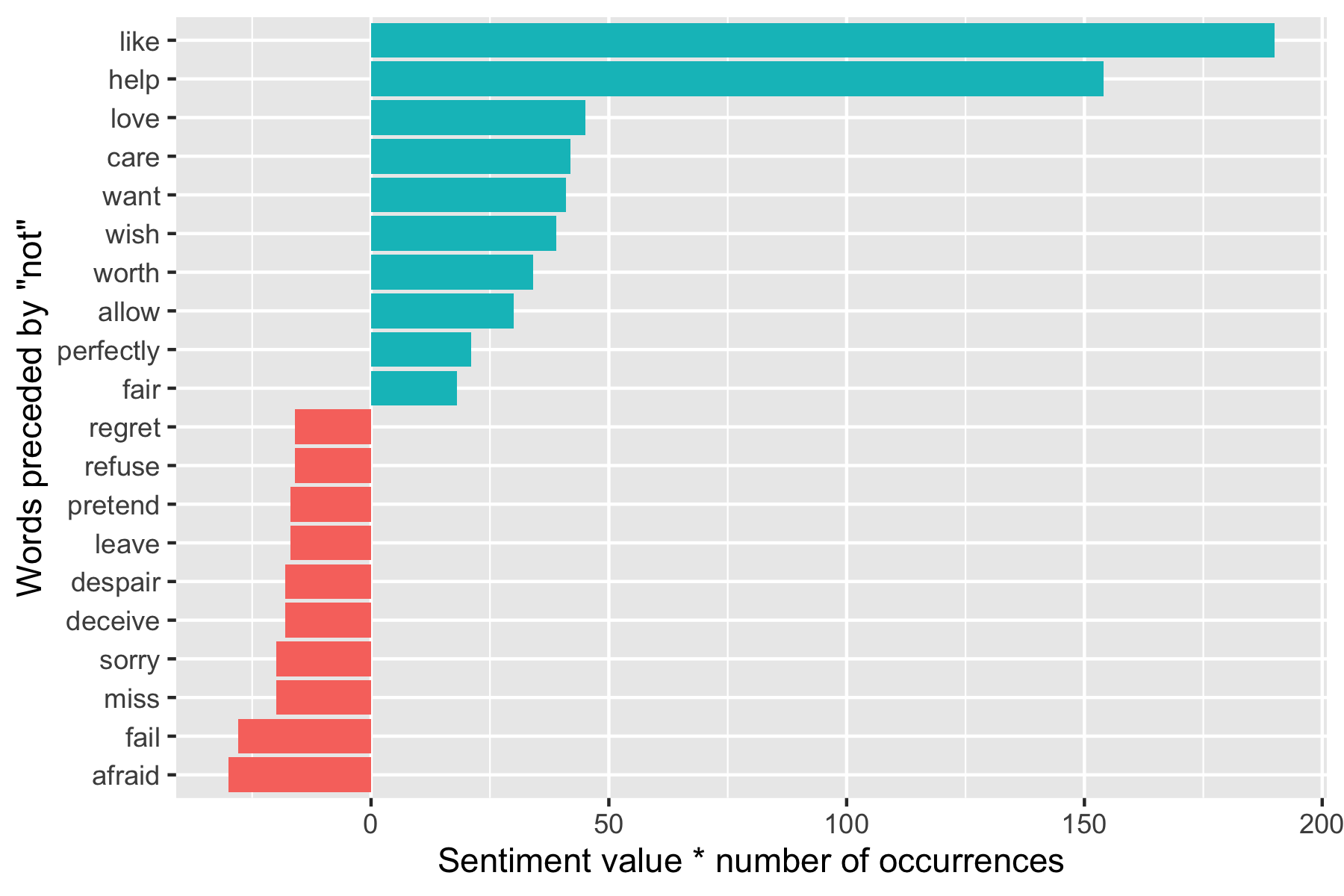
• The bigrams “not like” and “not help” make the text seem much more positive than it is.
• Phrases like “not afraid” and “not fail” sometimes suggest the text is more negative than it is.
• “Not” is not the only word that provides context for the following term.

Let’s pick four common words that negate the subsequent term and use the same joining and counting approach to examine all of them at once.

• Note: getting the sort right requires some workarounds.

negation_words <- c("not", "no", "never", "without")

bigrams_separated |>
  filter(word1 %in% negation_words) |>
  inner_join(AFINN, by = c(word2 = "word")) |>
  count(word1, word2, value, sort = TRUE) ->
negated_words

negated_words |>
  mutate(contribution = n * value) |>
  group_by(word1) |>
  slice_max(order_by = abs(contribution), n = 12) |>
  ungroup() |>
  ggplot(aes(reorder_within(word2, contribution, word1), n * value,
    fill = n * value > 0
  )) +
  geom_col(show.legend = FALSE) +
  xlab("Words preceded by negation term") +
  ylab("Sentiment value * Number of Occurrences") +
  coord_flip() +
  facet_wrap(~word1, scales = "free") +
  scale_x_discrete(labels = function(x) str_replace(x, "__.+$", ""))

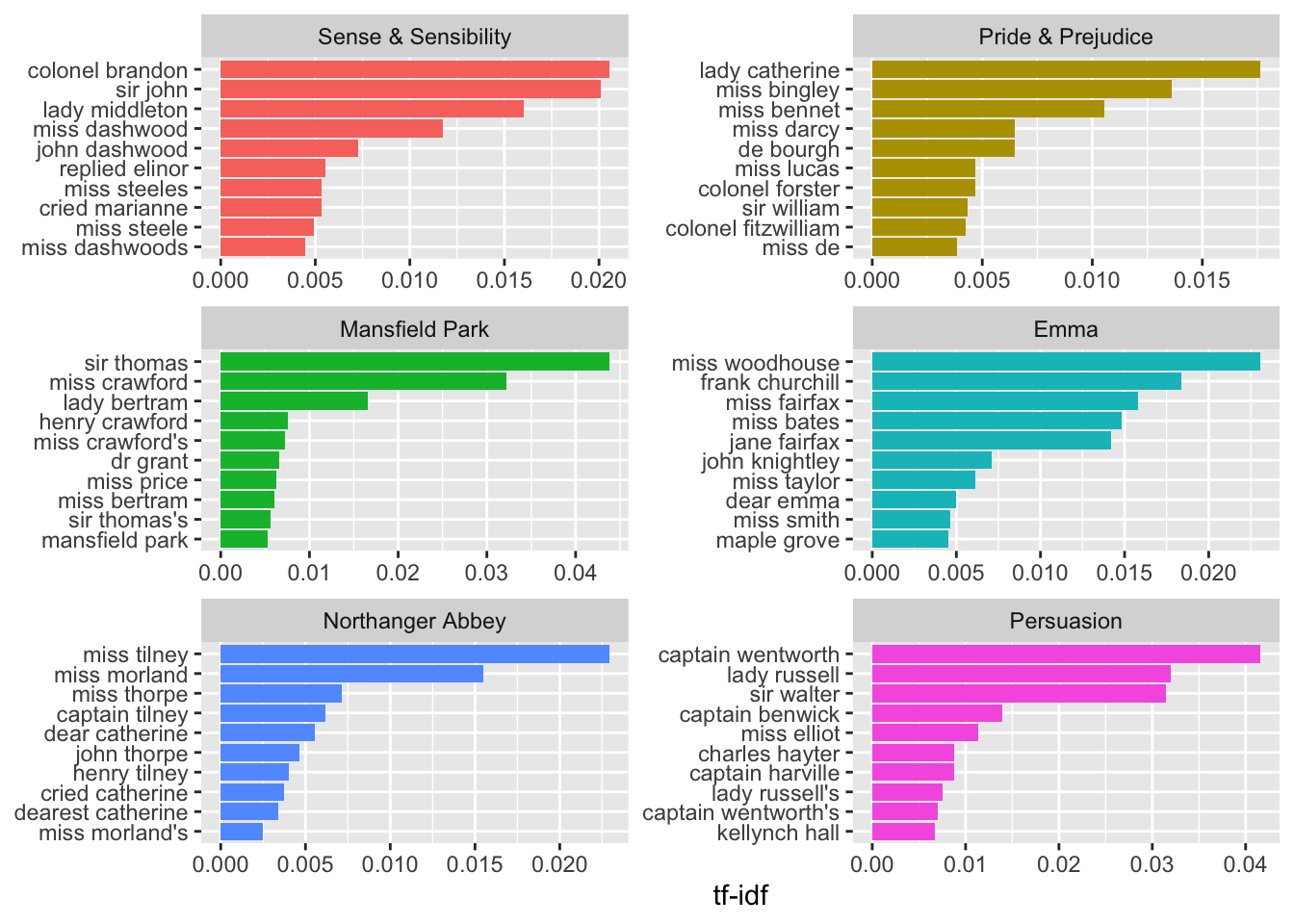
If you want to get more in depth with text analysis, suggest looking at the Readme for the Sentimentr Package.

16.3.5 Visualizing a Network of Bigrams with the {igraph}, and {ggraph} Packages

If you want to look at more than the top words, you can use a network-node graph to see all of the relationships among words simultaneously.

We can construct a network-node graph from a tidy object since it has three variables with the correct conceptual relationships:

• from: the node an edge is coming from,
• to: the node an edge is going towards, and
• weight: a numeric value associated with each edge.

The {igraph} package is an R package for network analysis.

• The main goal of the {igraph} package is to provide a set of data types and functions for

1. pain-free implementation of graph algorithms,
2. fast handling of large graphs, with millions of vertices and edges, and
3. allowing rapid prototyping via high-level languages like R.

One way to create an igraph object from tidy data is use the graph_from_data_frame() function.

It takes a data frame of edges, with columns for “from”, “to”, and edge attributes (in this case n from our original counts):

Use the console to install {igraph} and then load into the environment.

Take a look at our previously created bigram_counts.

library(igraph)
bigram_counts

# A tibble: 28,975 × 3
   word1   word2         n
   <chr>   <chr>     <int>
 1 <NA>    <NA>      12242
 2 sir     thomas      266
 3 miss    crawford    196
 4 captain wentworth   143
 5 miss    woodhouse   143
 6 frank   churchill   114
 7 lady    russell     110
 8 sir     walter      108
 9 lady    bertram     101
10 miss    fairfax      98
# ℹ 28,965 more rows

Let’s filter out NAs, get the top 20 combinations, and graph.

bigram_counts |>
  filter(n > 20, !is.na(word1), !is.na(word2)) |>
  graph_from_data_frame() ->
bigram_graph

bigram_graph

IGRAPH 236354a DN-- 85 70 -- 
+ attr: name (v/c), n (e/n)
+ edges from 236354a (vertex names):
 [1] sir     ->thomas     miss    ->crawford   captain ->wentworth 
 [4] miss    ->woodhouse  frank   ->churchill  lady    ->russell   
 [7] sir     ->walter     lady    ->bertram    miss    ->fairfax   
[10] colonel ->brandon    sir     ->john       miss    ->bates     
[13] jane    ->fairfax    lady    ->catherine  lady    ->middleton 
[16] miss    ->tilney     miss    ->bingley    thousand->pounds    
[19] miss    ->dashwood   dear    ->miss       miss    ->bennet    
[22] miss    ->morland    captain ->benwick    miss    ->smith     
+ ... omitted several edges

The {ggraph} package is an extension of {ggplot2} tailored to graph visualizations.

• It provides the same flexible approach to building up plots layer by layer.

Install with the console and load in this document.

To plot, we need to convert the igraph R object into a ggraph object with the ggraph() function

• We then add layers to it (as in ggplot2).

For a basic graph we need to add three layers: nodes, edges, and text.

• Given the use of randomized layouts we also set a random number seed for reproducibility.

  library(ggraph)
  set.seed(17)
  
  ggraph(bigram_graph, layout = "fr") + ##  The Fruchterman-Reingold layout
    geom_edge_link() +
    # geom_node_point() +
    geom_node_text(aes(label = name), vjust = 1, hjust = 1) +
    theme_void()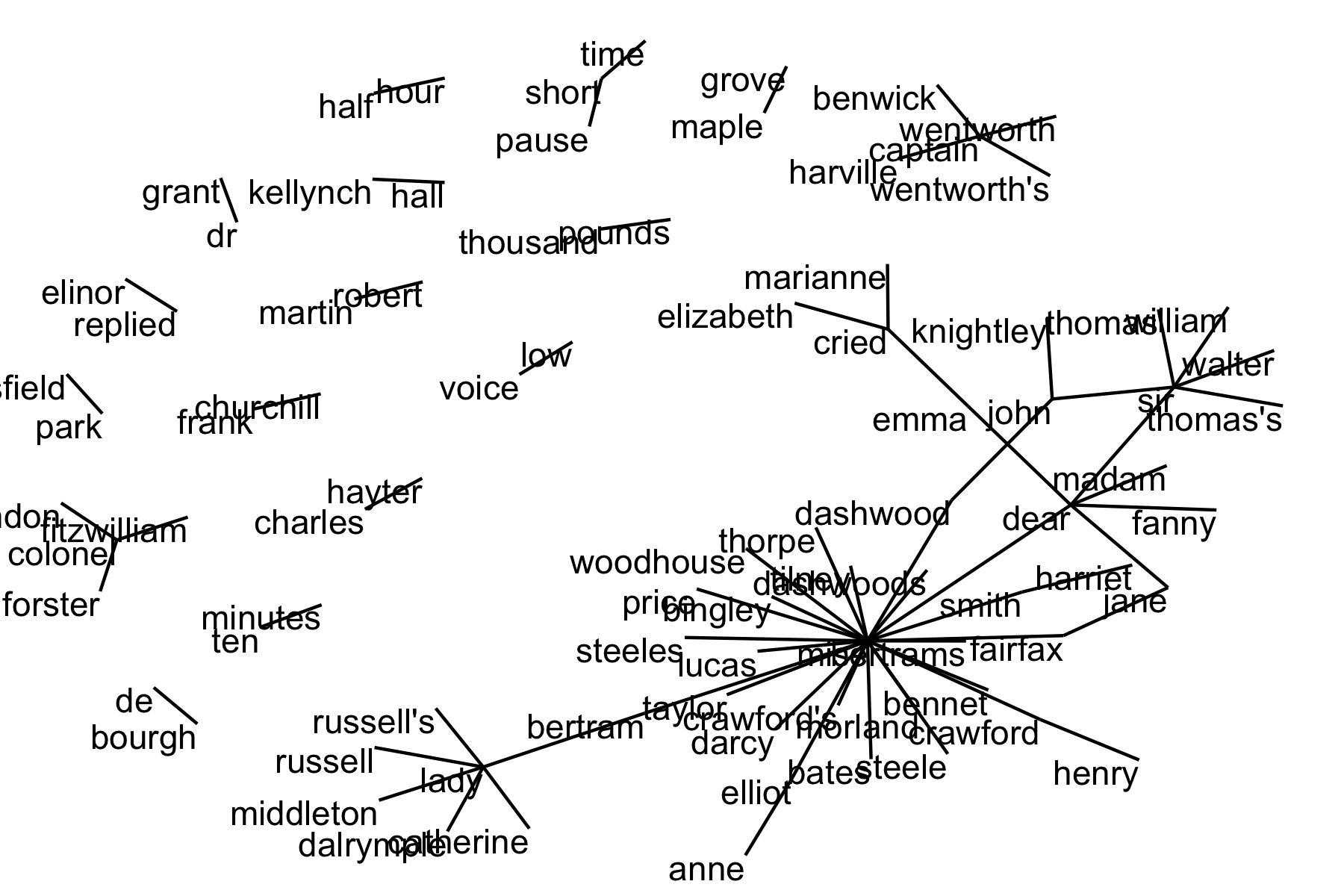

  

  ## With repel = TRUE
  ggraph(bigram_graph, layout = "fr") + ## The Fruchterman-Reingold layout
    geom_edge_link() +
    geom_node_point() +
    geom_node_text(aes(label = name), vjust = 1, hjust = 1, repel = TRUE) +
    theme_void()

  

If you want to do more analyses, the {widyr} package helps with other types of bigram analyses to include:

• Counting and correlating among sections.
• Checking pair-wise correlations.

16.4 Converting To and From Non-tidytext Formats

While tidytext format can support a lot of quick analyses, most R packages for NLP are not compatible with this format.

• They use sparse matrices for large amounts of text.

However, {tidytext} has functions that allow you to convert back and forth between formats as shown in the Figure 16.1 so you can work with other packages.

Figure 16.1: Tidytext workflows for various formats.

16.4.1 Tidying a document-term matrix (DTM)

One of the most common structures for NLP is the document-term matrix (or DTM).

• Each row represents one document (such as a book or article).
• Each column represents one term.
• Each value (typically) contains the number of appearances of the column term in the row document.

The {tidytext} package provides two functions to convert between DTM and tidytext formats.

• tidy() turns a DTM into a tidy data frame. This verb comes from the {broom} package.
• cast() turns a tidy one-term-per-row data frame into a matrix.
  • cast_sparse() converts to a sparse matrix (from the {Matrix} package),
  • cast_dtm() converts to a DTM object (from {tm}),
  • cast_dfm() (converts to a dfm object (from {quanteda}).

16.4.2 Tidying Document Term Matrix objects

Perhaps the most widely used implementation of DTMs in R is the DocumentTermMatrix class in the {tm} package.

• You can install with the console and load in the document.

Many available text mining datasets are provided in this format.

• For example, a collection of Associated Press newspaper articles is in the {topicmodels} package.

library(tm)
data("AssociatedPress", package = "topicmodels")
AssociatedPress

<<DocumentTermMatrix (documents: 2246, terms: 10473)>>
Non-/sparse entries: 302031/23220327
Sparsity           : 99%
Maximal term length: 18
Weighting          : term frequency (tf)

This is a DTM object on which we can use tidytext functions based on the {broom} package to do some format conversions.

• Note: documents * terms = 23,522,358 = non-sparse (302031) + number of sparse (23220327)

ap_td <- tidy(AssociatedPress)
ap_td

# A tibble: 302,031 × 3
   document term       count
      <int> <chr>      <dbl>
 1        1 adding         1
 2        1 adult          2
 3        1 ago            1
 4        1 alcohol        1
 5        1 allegedly      1
 6        1 allen          1
 7        1 apparently     2
 8        1 appeared       1
 9        1 arrested       1
10        1 assault        1
# ℹ 302,021 more rows

• Note: only the non-zero values are included in the tidied output

We can conduct sentiment analysis as before.

ap_td |>
  inner_join(get_sentiments("bing"), by = c(term = "word")) ->
ap_sentiments

ap_sentiments

# A tibble: 30,094 × 4
   document term    count sentiment
      <int> <chr>   <dbl> <chr>    
 1        1 assault     1 negative 
 2        1 complex     1 negative 
 3        1 death       1 negative 
 4        1 died        1 negative 
 5        1 good        2 positive 
 6        1 illness     1 negative 
 7        1 killed      2 negative 
 8        1 like        2 positive 
 9        1 liked       1 positive 
10        1 miracle     1 positive 
# ℹ 30,084 more rows

And plot as usual.

ap_sentiments |>
  count(sentiment, term, wt = count) |>
  filter(n >= 200) |>
  mutate(n = ifelse(sentiment == "negative", -n, n)) |>
  mutate(term = fct_reorder(term, n)) |>
  ggplot(aes(term, n, fill = sentiment)) +
  geom_bar(stat = "identity") +
  ylab("Contribution to sentiment") +
  coord_flip()

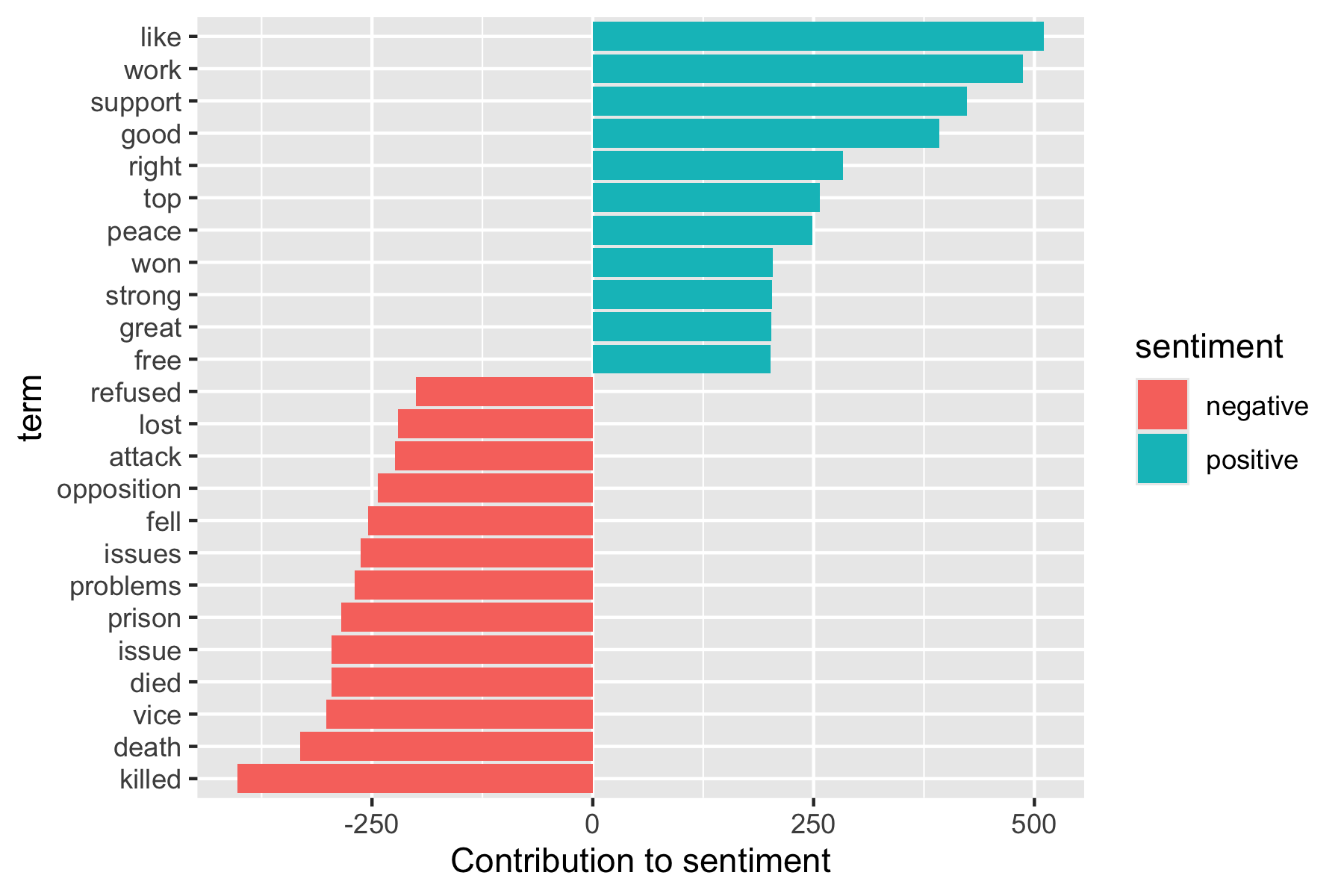
16.4.3 Tidying Document-Feature Matrix (DFM) objects

The DFM is an alternative implementation of DTM from the {quanteda} package.

The {quanteda} package comes with a corpus of presidential inauguration speeches, which can be converted to a class dfm object using the appropriate functions.

• As of version 3.0, you should tokenize the corpus first.

data("data_corpus_inaugural", package = "quanteda")
library(quanteda)
data_corpus_inaugural |>
  corpus_subset(Year > 1860) |>
  tokens() ->
toks
inaug_dfm <- quanteda::dfm(toks, verbose = FALSE)
inaug_dfm

Document-feature matrix of: 41 documents, 7,750 features (90.42% sparse) and 4 docvars.
               features
docs            fellow-citizens  of the united states : in compliance with  a
  1861-Lincoln                1 146 256      5     19 5 77          1   20 56
  1865-Lincoln                0  22  58      0      0 1  9          0    8  7
  1869-Grant                  0  47  83      3      3 1 27          0   10 19
  1873-Grant                  1  72 106      0      3 2 26          0    9 21
  1877-Hayes                  0 166 240      7     11 0 63          1   19 41
  1881-Garfield               2 181 317      7     15 1 49          0   19 35
[ reached max_ndoc ... 35 more documents, reached max_nfeat ... 7,740 more features ]

The {tidytext} implementation of tidy() works here as well.

inaug_td <- tidy(inaug_dfm)
arrange(inaug_td, term, desc= TRUE)

# A tibble: 30,440 × 3
   document       term  count
   <chr>          <chr> <dbl>
 1 1901-McKinley  "!"       1
 2 1913-Wilson    "!"       1
 3 1937-Roosevelt "!"       1
 4 2009-Obama     "!"       1
 5 1861-Lincoln   "\""     10
 6 1865-Lincoln   "\""      4
 7 1877-Hayes     "\""      2
 8 1881-Garfield  "\""      8
 9 1885-Cleveland "\""      6
10 1889-Harrison  "\""      2
# ℹ 30,430 more rows

We see some punctuation here.

Let’s remove the the terms that are solely punctuation.

inaug_td |> 
  filter(str_detect(term, "^[:punct:]$", negate = TRUE)) ->
  inaug_td

To find words most specific to each of the inaugural speeches we can use tf-idf for each term-speech pair using the bind_tf_idf() function.

inaug_tf_idf <- inaug_td |>
  bind_tf_idf(term, document, count) |>
  arrange(desc(tf_idf))

inaug_tf_idf

# A tibble: 30,181 × 6
   document       term     count      tf   idf tf_idf
   <chr>          <chr>    <dbl>   <dbl> <dbl>  <dbl>
 1 1865-Lincoln   woe          3 0.00429  3.71 0.0159
 2 1865-Lincoln   offenses     3 0.00429  3.71 0.0159
 3 1945-Roosevelt learned      5 0.00898  1.63 0.0147
 4 1961-Kennedy   sides        8 0.00586  2.10 0.0123
 5 1869-Grant     dollar       5 0.00444  2.61 0.0116
 6 1905-Roosevelt regards      3 0.00305  3.71 0.0113
 7 2001-Bush      story        9 0.00568  1.92 0.0109
 8 1945-Roosevelt trend        2 0.00359  3.02 0.0108
 9 1965-Johnson   covenant     6 0.00403  2.61 0.0105
10 1945-Roosevelt test         3 0.00539  1.92 0.0104
# ℹ 30,171 more rows

inaug_tf_idf |>
  filter(document %in% c(
    "1861-Lincoln", "1933-Roosevelt", "1961-Kennedy",
    "2009-Obama", "2017-Trump", "2021-Biden"
  )) |>
  mutate(term = str_extract(term, "[a-z']+")) |>
  group_by(document) |>
  arrange(desc(tf_idf)) |>
  slice_max(order_by = tf_idf, n = 10) |>
  ungroup() |>
  ggplot(aes(
    x = reorder_within(term, tf_idf, document),
    y = tf_idf, fill = document
  )) +
  geom_col(show.legend = FALSE) +
  facet_wrap(~document, scales = "free") +
  coord_flip() +
  scale_x_discrete(labels = function(x) str_replace(x, "__.+$", ""))

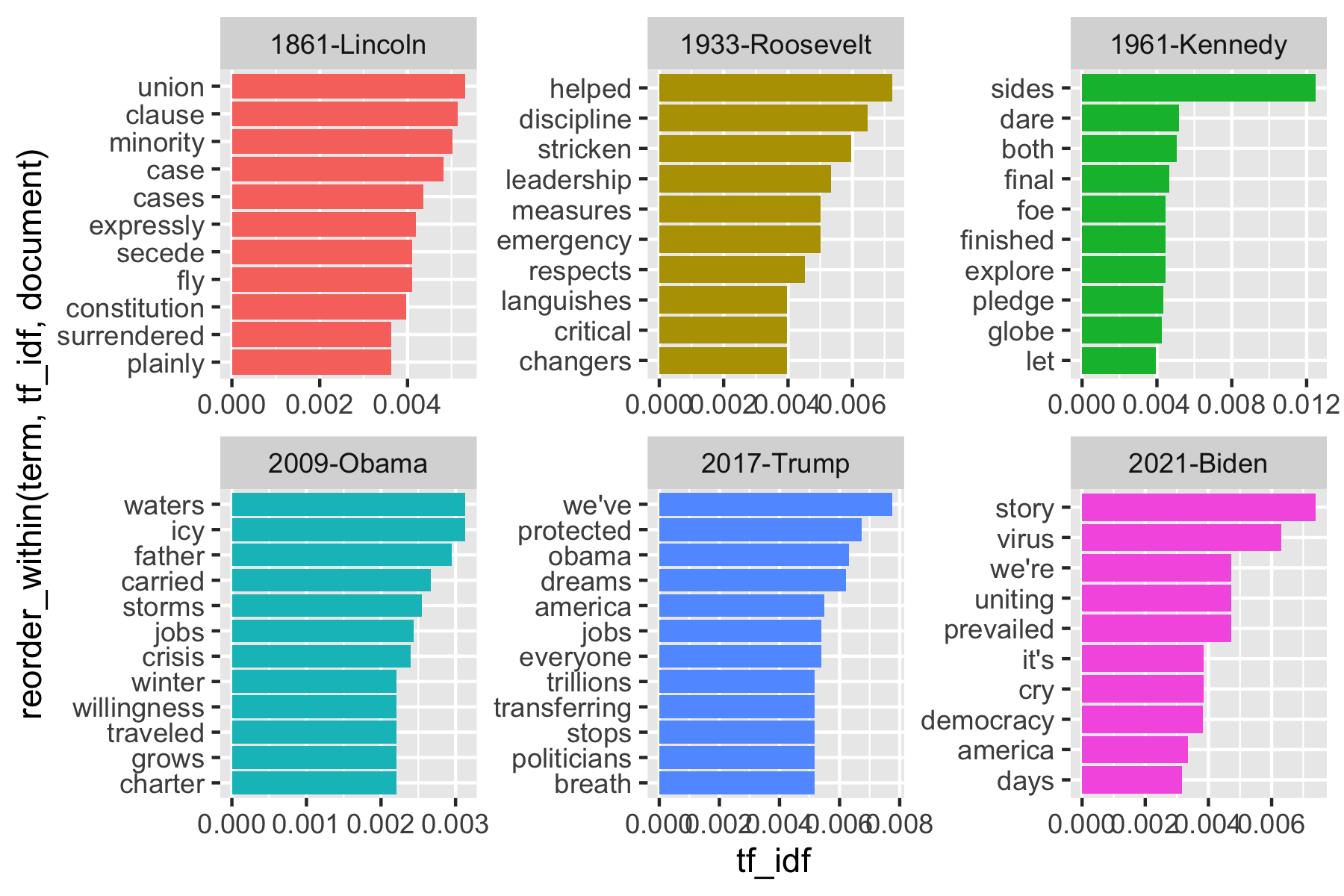
16.4.4 Casting tidy text Data into a Matrix using cast()

We can also go the other way: convert tidytext format to a matrix.

Let’s convert the tidied AP dataset back into a DTM using the cast_dtm() function.

ap_td |>
  cast_dtm(document, term, count)

<<DocumentTermMatrix (documents: 2246, terms: 10473)>>
Non-/sparse entries: 302031/23220327
Sparsity           : 99%
Maximal term length: 18
Weighting          : term frequency (tf)

• Similarly, we could cast the table into a dfm object from {quanteda} dfm with cast_dfm().

ap_td |>
  cast_dfm(document, term, count)

Document-feature matrix of: 2,246 documents, 10,473 features (98.72% sparse) and 0 docvars.
    features
docs adding adult ago alcohol allegedly allen apparently appeared arrested
   1      1     2   1       1         1     1          2        1        1
   2      0     0   0       0         0     0          0        1        0
   3      0     0   1       0         0     0          0        1        0
   4      0     0   3       0         0     0          0        0        0
   5      0     0   0       0         0     0          0        0        0
   6      0     0   2       0         0     0          0        0        0
    features
docs assault
   1       1
   2       0
   3       0
   4       0
   5       0
   6       0
[ reached max_ndoc ... 2,240 more documents, reached max_nfeat ... 10,463 more features ]

16.4.5 Tidying Corpus Objects with Metadata

The corpus data structure can contain documents before tokenization along with metadata.

For example, the {tm} package comes with the acq corpus, containing 50 articles from the news service Reuters.

data("acq")
acq

<<VCorpus>>
Metadata:  corpus specific: 0, document level (indexed): 0
Content:  documents: 50

A corpus object is structured like a list, with each item containing both text and metadata.

We can use tidy() to construct a table with one row per document, including the metadata (such as id and datetimestamp) as columns alongside the text.

acq_td <- tidy(acq)
acq_td

# A tibble: 50 × 16
   author   datetimestamp       description heading id    language origin topics
   <chr>    <dttm>              <chr>       <chr>   <chr> <chr>    <chr>  <chr> 
 1 <NA>     1987-02-26 15:18:06 ""          COMPUT… 10    en       Reute… YES   
 2 <NA>     1987-02-26 15:19:15 ""          OHIO M… 12    en       Reute… YES   
 3 <NA>     1987-02-26 15:49:56 ""          MCLEAN… 44    en       Reute… YES   
 4 By Cal … 1987-02-26 15:51:17 ""          CHEMLA… 45    en       Reute… YES   
 5 <NA>     1987-02-26 16:08:33 ""          <COFAB… 68    en       Reute… YES   
 6 <NA>     1987-02-26 16:32:37 ""          INVEST… 96    en       Reute… YES   
 7 By Patt… 1987-02-26 16:43:13 ""          AMERIC… 110   en       Reute… YES   
 8 <NA>     1987-02-26 16:59:25 ""          HONG K… 125   en       Reute… YES   
 9 <NA>     1987-02-26 17:01:28 ""          LIEBER… 128   en       Reute… YES   
10 <NA>     1987-02-26 17:08:27 ""          GULF A… 134   en       Reute… YES   
# ℹ 40 more rows
# ℹ 8 more variables: lewissplit <chr>, cgisplit <chr>, oldid <chr>,
#   places <named list>, people <lgl>, orgs <lgl>, exchanges <lgl>, text <chr>

We can then unnest_tokens(), for example, to find the most common words across the 50 Reuters articles.

acq_tokens <- acq_td |>
  select(-places) |>
  unnest_tokens(word, text) |>
  anti_join(stop_words, by = "word")

## most common words
acq_tokens |>
  count(word, sort = TRUE)

# A tibble: 1,566 × 2
   word         n
   <chr>    <int>
 1 dlrs       100
 2 pct         70
 3 mln         65
 4 company     63
 5 shares      52
 6 reuter      50
 7 stock       46
 8 offer       34
 9 share       34
10 american    28
# ℹ 1,556 more rows

Or the words most specific to each article (by id).

## tf-idf
acq_tokens |>
  count(id, word) |>
  bind_tf_idf(word, id, n) |>
  arrange(desc(tf_idf))

# A tibble: 2,853 × 6
   id    word         n     tf   idf tf_idf
   <chr> <chr>    <int>  <dbl> <dbl>  <dbl>
 1 186   groupe       2 0.133   3.91  0.522
 2 128   liebert      3 0.130   3.91  0.510
 3 474   esselte      5 0.109   3.91  0.425
 4 371   burdett      6 0.103   3.91  0.405
 5 442   hazleton     4 0.103   3.91  0.401
 6 199   circuit      5 0.102   3.91  0.399
 7 162   suffield     2 0.1     3.91  0.391
 8 498   west         3 0.1     3.91  0.391
 9 441   rmj          8 0.121   3.22  0.390
10 467   nursery      3 0.0968  3.91  0.379
# ℹ 2,843 more rows

16.4.6 Format Conversion Summary

Text analysis requires working with a variety of tools, many of which use non-tidytext formats.

You can use tidytext functions to convert between a tidy text data frame and other formats such as DTM, DFM, and Corpus objects containing document metadata to facilitate your own work or collaboration with others.

Bates, Douglas, Martin Maechler, and Mikael Jagan. 2023. “Matrix Package (Base R Install).” https://cran.r-project.org/web/packages/Matrix/index.html.

Benoit, Kenneth, Kohei Watanabe, Haiyan Wang, Paul Nulty, Adam Obeng, and Stefan Mul. 2018. “Quanteda: An R Package for the Quantitative Analysis of Textual Data.” JOSS 3 (30): 774. https://doi.org/10.21105/joss.00774.

Csardi, Garbor, Tamas Nepusz, Vincent Tragg, Szabolcs Horvat, Fabio Zanini, Daniel Noom, and Kirill Muller. 2023. “Igraph: Network Analysis and Visualization in R.” https://doi.org/10.5281/zenodo.7682609.

Feinerer, Ingo, and Kurt Hornik. 2023. “Tm - Text Mining Package.” https://tm.r-forge.r-project.org/.

Grün, Bettina, and Kurt Hornik. 2023. “Topicmodels: Topic Models.” https://cran.r-project.org/web/packages/topicmodels/index.html.

Pedersen, Thomas Lin. 2022. “Ggraph: An Implementation of Grammar of Graphics for Graphs and Networks.” https://ggraph.data-imaginist.com/.

Rinker, Tyler. 2018. “Sentimentr.” https://github.com/trinker/sentimentr.

Robinson, David, and Julia Silge. 2022. “Widyr: An R Package to Widen, Process, and Re-Tidy a Dataset.” https://juliasilge.github.io/widyr/.

Selivanov, Dimitriy. 2023. “Text2vec.” http://text2vec.org/.

Silge, Julia. 2023. “Janeaustenr.” https://github.com/juliasilge/janeaustenr.

Silge, Julia, and David Robinson. 2016. “Tidytext: Text Mining and Analysis Using Tidy Data Principles in R.” The Open Journal JOSS 1 (3). https://doi.org/10.21105/joss.00037.

———. 2022. Tidytext: Text Mining with R. O’Reilly Media, Inc. https://www.tidytextmining.com/.

———. 2023a. “Tidytext: Text Mining Using Tidy Tools.” https://juliasilge.github.io/tidytext/.

———. 2023b. “Tidytext: GitHub.” https://github.com/juliasilge/tidytext.

“Word2vec Package.” 2023. bnosac. https://github.com/bnosac/word2vec.