8  Tree Methods

Author
Affiliation

Richard Ressler

American University

Published

September 14, 2024

8.1 Why Trees

Trees are popular because they are intuitive and easy to understand.

  • Certainly easier than principal components with its uninterpretable linear combinations.
  • However, this can come at a cost of lower performance.

Let’s try an example of making a decision - Do we want to buy a given house?

We start by asking a series of yes-no questions.

  • Is it affordable - yes or no?
  • For each response we make a decision: Buy if Yes, or if No, ask another question.
  • We ask as many questions as we need to make a final decision.
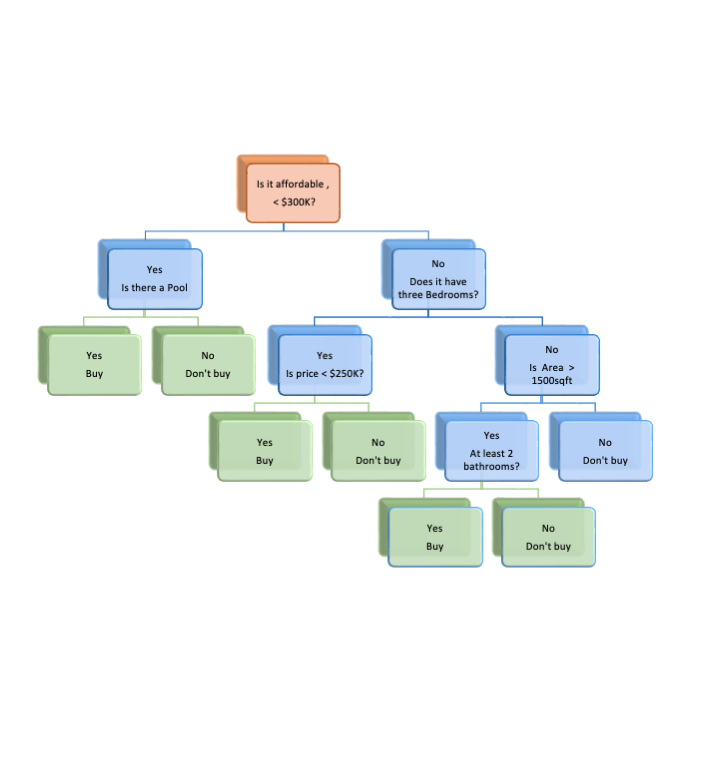
Figure 8.1: A decision tree for buying a house.

The (upside-down) tree in Figure 8.1 represents the way many people think they make decisions.

  • They examine alternatives one by one and make a “rational” choice.

8.2 The Structure of Trees

  • A tree has a root.
  • It splits into branches.
  • Each split is a node.
  • A node with no splits (lowest on its branch), where we make a final decision, is called a terminal node or a leaf.

8.3 Types of Trees

There are Classification Trees and Regression Trees.

Classification Trees predict a categorical response.

  • Buy the house or not?
  • They are not limited to just binary responses.

Regression Trees predict a quantitative response.

  • How much is a fair price for the house?
  • At every internal node, it decides how to split for the best prediction.

People use analogies such as “growing” and “pruning” to describe creating the splits and then removing splits to trim the size of the tree (to avoid overfitting).

Important

At each internal node you choose two things

  • A variable
  • A threshold for the variable to provide the best prediction (the decision).

Every terminal node \(m\) will make one prediction, a \(\hat{Y}_m\) for all the sampling units (\(X_j\)) remaining in the \(m\)th node.

For regression trees, \(\hat{y}_m\) is the sample mean of all the responses that fit in the \(m\)th node.

For classification trees, use “majority rules” (like KNN) so \(\hat{y}_m\) is the most frequent response of all the responses that fit in the \(m\)th node. It’s the mode of the responses remaining in the node.

8.4 Trees in R with {tree}

8.4.1 Fitting and Plotting Trees

The R {tree} package has functions for fitting and plotting trees.

Let’s start with fitting the HOMES_SALES data.

Show code
library(tree)

Download the HOME_SALES data from https://raw.githubusercontent.com/rressler/data_raw_courses/main/HOME_SALES.csv

Show code
homes <- read_csv("https://raw.githubusercontent.com/rressler/data_raw_courses/main/HOME_SALES.csv")
glimpse(homes)
Rows: 522
Columns: 13
$ ID              <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ SALES_PRICE     <dbl> 360000, 340000, 250000, 205500, 275500, 248000, 229900…
$ FINISHED_AREA   <dbl> 3032, 2058, 1780, 1638, 2196, 1966, 2216, 1597, 1622, …
$ BEDROOMS        <dbl> 4, 4, 4, 4, 4, 4, 3, 2, 3, 3, 7, 3, 5, 5, 3, 5, 2, 3, …
$ BATHROOMS       <dbl> 4, 2, 3, 2, 3, 3, 2, 1, 2, 3, 5, 4, 4, 4, 3, 5, 2, 4, …
$ GARAGE_SIZE     <dbl> 2, 2, 2, 2, 2, 5, 2, 1, 2, 1, 2, 3, 3, 2, 2, 2, 2, 2, …
$ YEAR_BUILT      <dbl> 1972, 1976, 1980, 1963, 1968, 1972, 1972, 1955, 1975, …
$ STYLE           <dbl> 1, 1, 1, 1, 7, 1, 7, 1, 1, 1, 7, 1, 7, 5, 1, 6, 1, 7, …
$ LOT_SIZE        <dbl> 22221, 22912, 21345, 17342, 21786, 18902, 18639, 22112…
$ AIR_CONDITIONER <chr> "YES", "YES", "YES", "YES", "YES", "YES", "YES", "YES"…
$ POOL            <chr> "NO", "NO", "NO", "NO", "NO", "YES", "NO", "NO", "NO",…
$ QUALITY         <chr> "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MED…
$ HIGHWAY         <chr> "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", …

Recall that QUALITY has three levels.

Show code
unique(homes$QUALITY)
[1] "MEDIUM" "LOW"    "HIGH"

Let’s predict house quality as a function of the other variables.

Let’s build/fit a classification tree and plot it.

Show code
tr <- tree(as.factor(QUALITY) ~ ., data = homes)
plot(tr)

We get a plot, but it’s hard to interpret as is.

Let’s add some text

Show code
plot(tr)
text(tr)

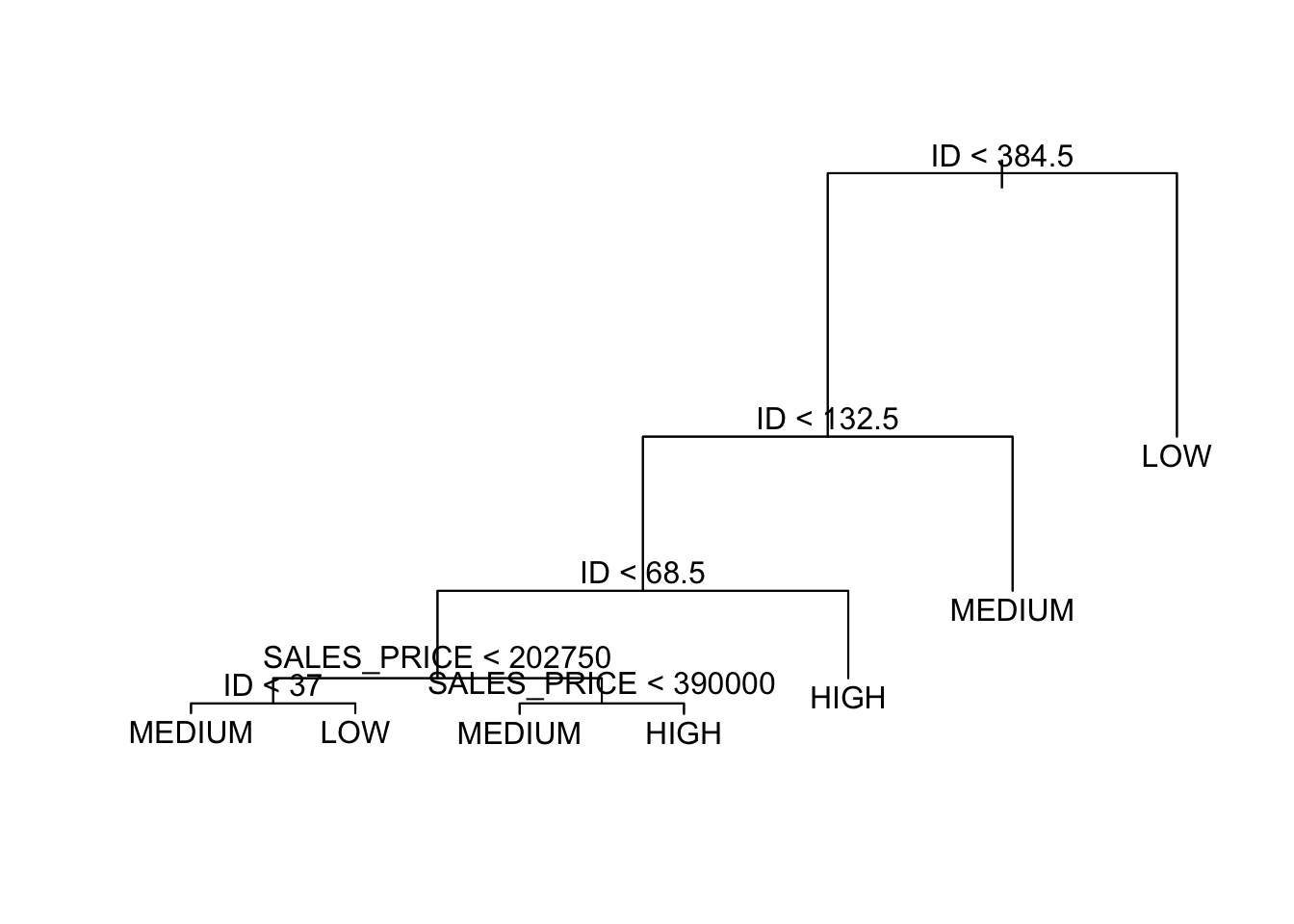
What do you think it means that ID seems so important?

  • This data set happens to have high quality houses lower in the the order.
  • That suggests the tree would do poorly predicting new data that happened to be in a different order or even have a different number of rows of each kind of quality.

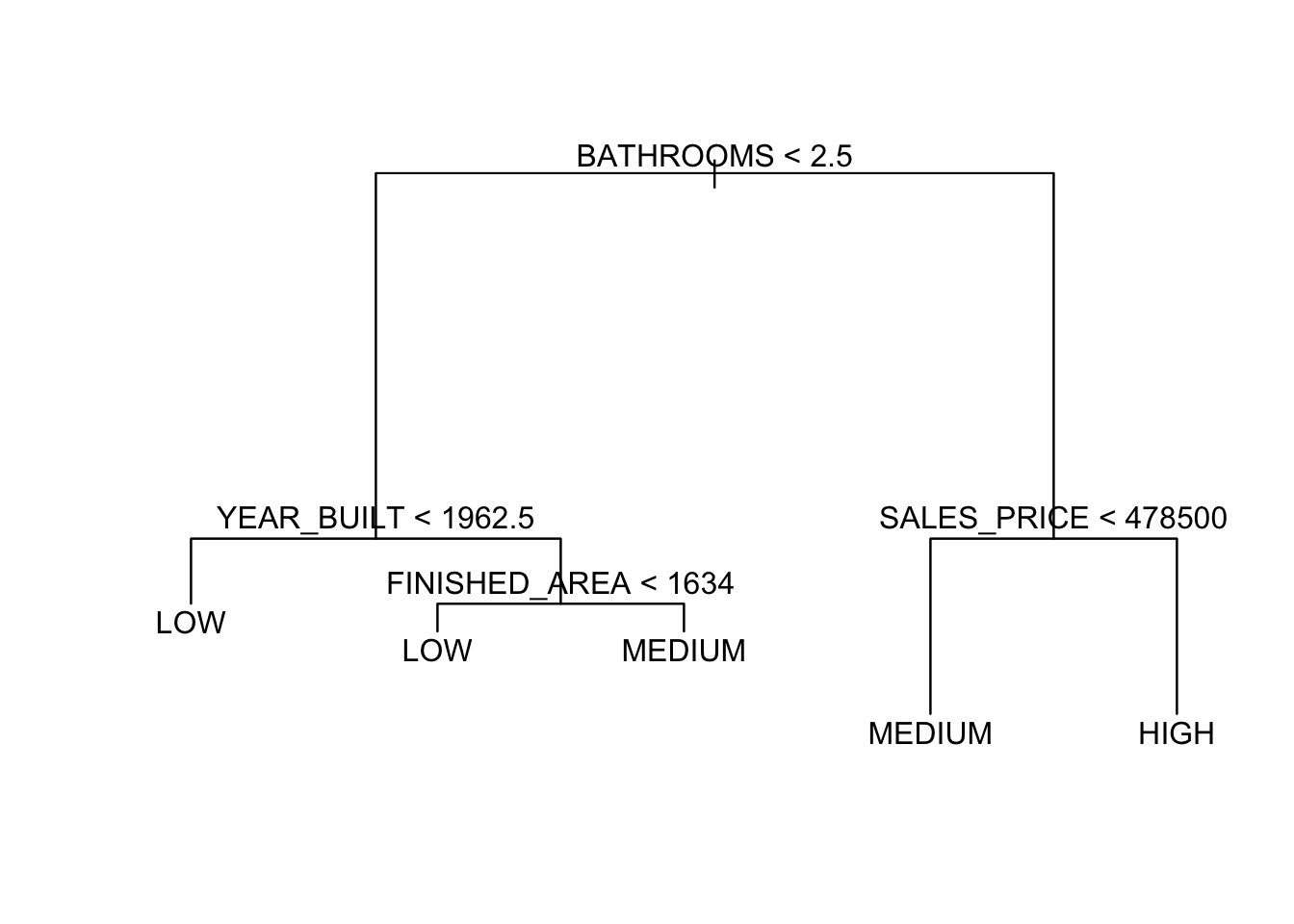
Let’s refit without ID.

Show code
tr <- tree(as.factor(QUALITY) ~ . - ID, data = homes)
plot(tr)
text(tr)

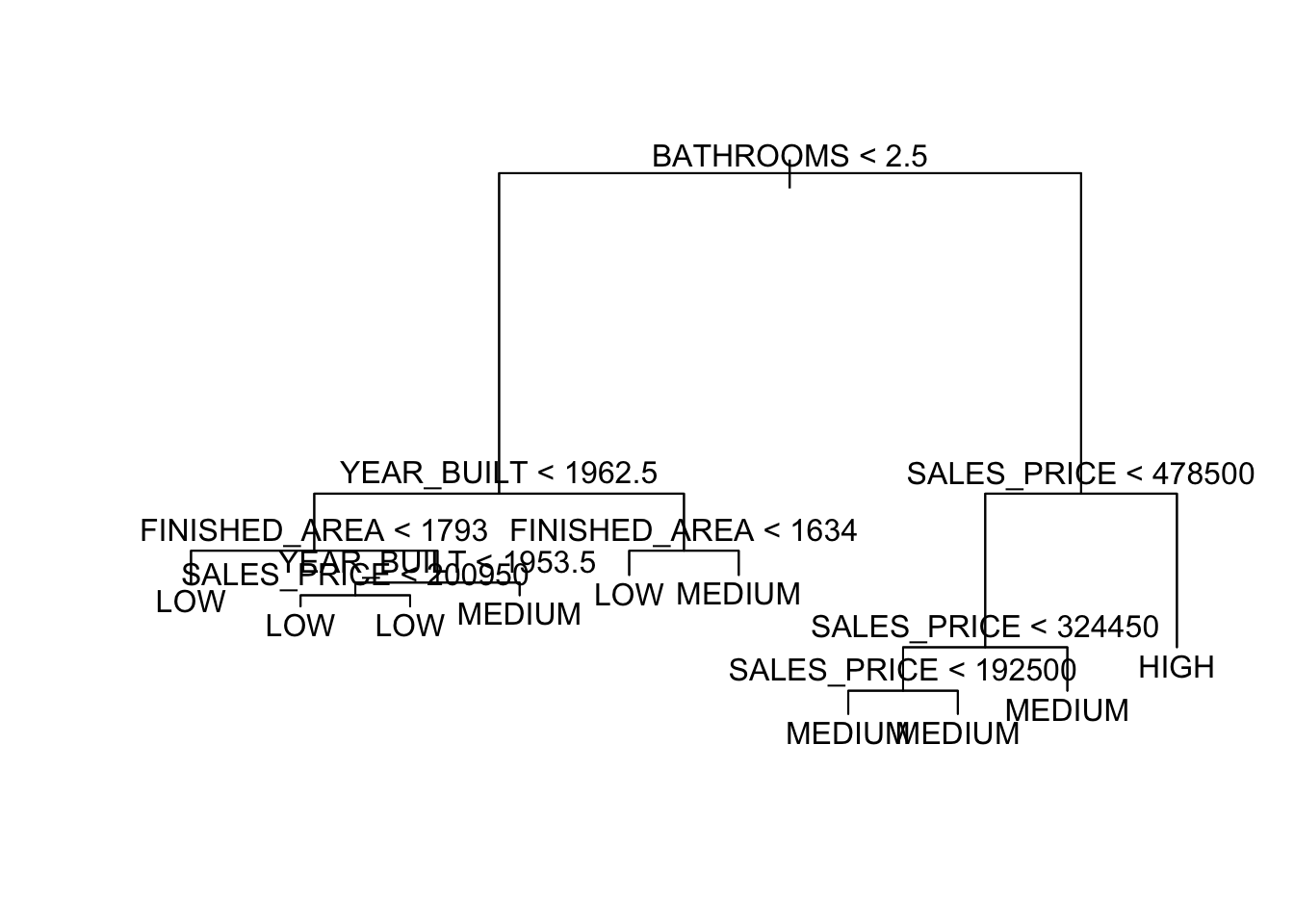
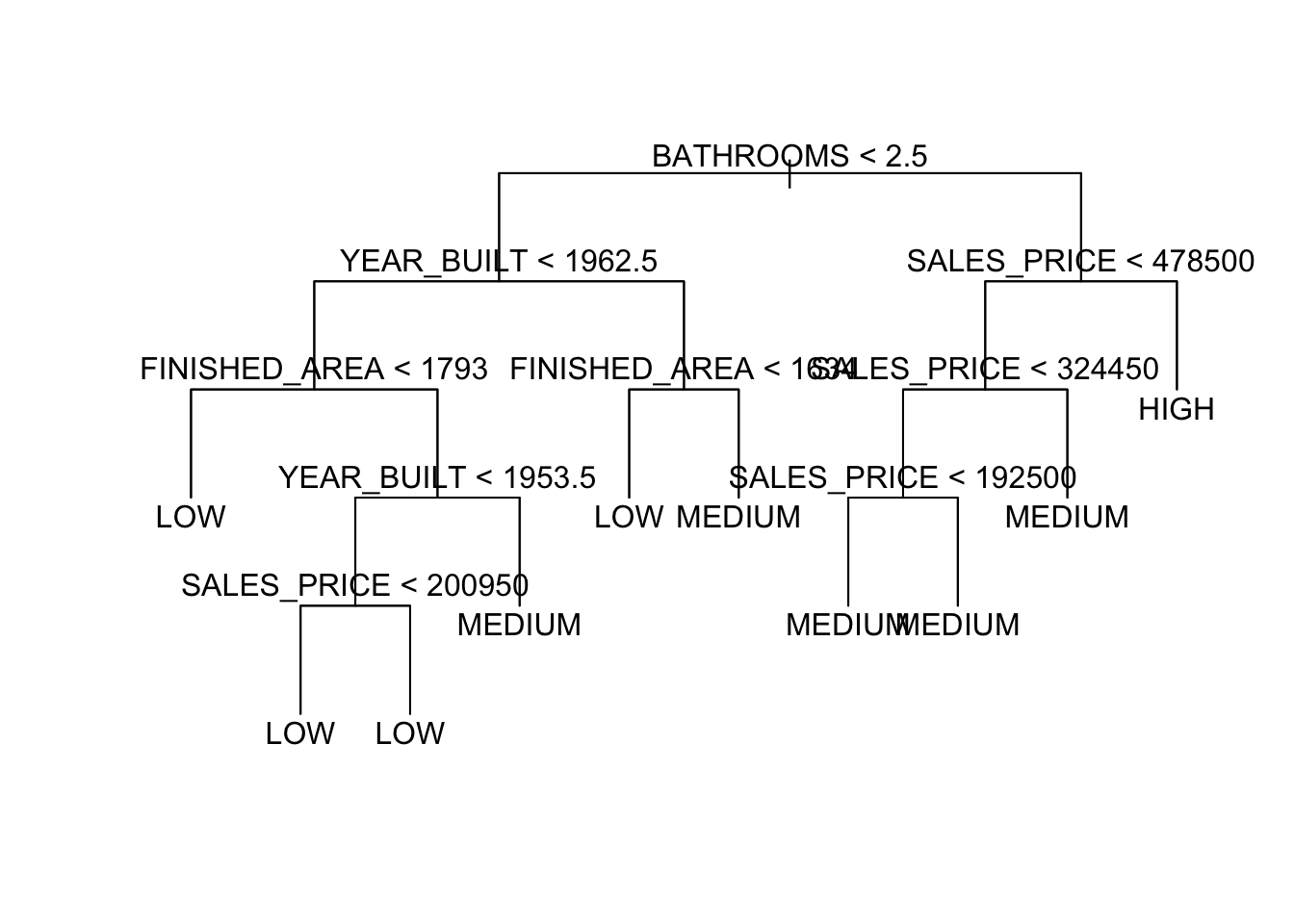
We get a much different tree.

To interpret the tree, start at the top, at the root node.

  • The variable at the root node is the one that offers the most contribution to making the prediction.
  • The variable is identified as is the threshold for the logical comparison.
    • If TRUE, then go left.
    • If FALSE then go right.
  • The height of the vertical lines below each split node indicates the contribution of the split to reducing the “impurity” in the set of resultant leaf nodes.
    • You expect the lines to get shorter as you go down the tree.

If you just want to see the results, without the line lengths meaning anything (better readability), you can plot with type = "uniform.

Show code
plot(tr, type = "uniform")
text(tr)

8.4.2 Choosing the Splits

For regression trees, the splits are chosen to maximize the reduction in the error sum of squares explained by the split so the line lengths represent that relative reduction.

  • Longer lines means more of the error was explained.

For classification trees, the splits are chosen to maximize the reduction in the Gini Impurity Index across the resultant leaf nodes.

  • This index is not quite the same as the Gini Coefficient used in social sciences, e.g., as a measure of income inequality within a population, but it is named after the same mathematician.
  • The tree::tree() function uses the Classification and Regression Trees (CART) algorithm for deciding how to make a split on a classification tree (there are other algorithms).
  • This algorithm computes the impurity index based on how often a randomly chosen element from the set would be incorrectly labeled if it was randomly labeled according to the distribution of labels in the subset.
    • Compute the index \(I_G(p)\) by summing the probability of class \(i\) being chosen, \(p_i\), times the probability of a mistake in categorizing that item \(\sum_{k \neq i}p_{k}=1-p_i\)
    • For \(M\) classes, where \(i \in \{1, \ldots, M\}\) and \(p_i\) is the proportion of items labeled with class \(i\) at the node, then calculate the index as:

\[ I_{G}(p) = \sum_{i=1}^{M}\left(p_i\sum_{k\neq i}p_k\right) = 1-\sum_{i=1}^M p_i^2 \]

  • Repeat for each node created by the split to make new leaf nodes.
  • To get the result for a split, create a weighted sum of the indices across the two resultant leaf nodes where the weights are the number of observations in each leaf node.

\[ I_{G}(Split) = \frac{n_{Left}I_{G}(Left) + n_{Right}I_{G}(Right) }{n_{Left} + n_{Right}} \]

  • The algorithm can reuse variables on multiple nodes, but with different thresholds.
  • If all the responses at a node are of the same class, then \(p_i = 1\) so \(I_G(p) = 0\) and that node cannot be split any more. That node remains a leaf node.

As more splits occur, the nodes become more pure.

  • It is not required that every leaf-node be pure as we may want to tune (trim) to get close enough and avoid overfitting.

An example of Choosing a Split.

A split node has 10 categorical observations as follows.

  • Class 1: X1 values: 2, 3, 5
  • Class 2: X1 values 3, 5, 7, 8
  • Class 3: X1 values 5, 6, 9

What is the probability of each class being chosen?

  • Class 1: \(3/(3 + 4 + 3) = 3/10 = 0.3\)
  • Class 2: \(4/10 = 0.4\)
  • Class 3: \(3/10 = 0.3\)

\(\sum_{i=i}^3p(i) = 1\).

What is the probability of being misclassified?

  • Class 1: \((4 + 3)/(10) = 1 - (3/10) = 0.7\)
  • Class 2: \((3+3)/10 = 0.6\)
  • Class 3: \((3+4)/10 = 0.7\)

So p(misclassified)\(_i\) = \(\sum_{k\neq i}^M p_k\)

What is the Gini Impurity Index for this node?

The Gini index for the node (before split) is the sum of the pairwise probabilities for each class.

\[ \begin{align} I_G(Node) &= \sum_{i=1}^3\left(p_i \sum_{k\neq i}^3(1-p_k)\right) = 1 - \sum_{i=1}^3 p_i^2\\ \\ I_G (Node) &= 1-(.09 +.16 +.09) = 1 - .34 = .66 \end{align} \]

Compare possible splits at X1 \(\leq5\) and X1 \(\leq 6\)

Consider a split at 5

Calculate the impurity (or cost) of each split as a weighted sum of the \(I_G\) for each side.

  • Left side of the split (\(X1 \leq5\)) has a total of 3, 2, and 1 observations in each class and the right side (\(X1>5\)) has 0, 2, and 2 observations in each class.
  • \(I_G(Left) = 1- ((3/6)^2 + (2/6)^2 + (1/6)^2) = 1 - (9 + 4 + 1)/36 = .61\)
  • \(I_G(Right) = 1- ((0/4)^2 + (2/4)^2 + (2/4)^2) = 1 - (0+ 4 + 4)/16 = .5\)
  • Combine them in a weighted average to get the Impurity of (split at 5) = \(I_G(5)=(6/10)*.61 + (4/10)*.5 = .566\)

Consider a split at 6

Calculate the impurity (or cost) of each split as a weighted sum of the \(I_G\) for each side.

  • Left has 3, 2, 2 observations in each class, Right has 0, 1, 2 observations in each class.
  • \(I_G(Left) = 1- ((3/7)^2 + (2/7)^2 + (2/7)^2) = 1 - (9 + 4 + 4)/49 = .65\)
  • \(I_G(Right) = 1- ((0/3)^2 + (1/3)^2 + (2/3)^2) = 1 - (0+ 1 + 4)/9 = .56\)
  • Combine them in a weighted average to get the Impurity of (split at 6) = \(I_G(6)=(7/10) *.65 + (3/10)*.55 = .62\)

Notice both \(I_G(5)< I_G(Node)\) and \(I_G(6)< I_G(Node)\).

\(I_G(5)=.565 < I_G(6)=.620\) so Split at 5 has less impurity so would choose that one. Would need to compare all the other possible splits (2, 3, 7, 8, 9) as well before making the final choice.

8.4.3 Measuring Performance of Trees in R

The detailed structure of the tree is in the frame element of the tree() output, here tr$frame.

  • The default display of the model object shows you the contents of frame.
  • It shows the structure using indentation.
    • It’s a data frame, but you have to View() it to see it as a table.
  • Each row indicates a node on the tree
    • var is variable used at the split.
    • n is the number of cases reaching that node (may be weighted).
    • dev is the deviance remaining at that node.
    • yval is the \(\hat{y}\) that would be predicted if it were a leaf node.
    • Columns for the number of levels with the associated proportions \(p_i\) at that node.
      • Multiplying n by the proportions gives the number of observations of each level in the node.
    • An asterisk indicates a terminal or leaf node.
    Show code
    tr
    node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 522 997.90 MEDIUM ( 0.130268 0.314176 0.555556 )  
   2) BATHROOMS < 2.5 243 326.70 LOW ( 0.004115 0.646091 0.349794 )  
     4) YEAR_BUILT < 1962.5 174 180.10 LOW ( 0.000000 0.787356 0.212644 )  
       8) FINISHED_AREA < 1793 110  62.30 LOW ( 0.000000 0.918182 0.081818 ) *
       9) FINISHED_AREA > 1793 64  87.72 LOW ( 0.000000 0.562500 0.437500 )  
        18) YEAR_BUILT < 1953.5 29  29.57 LOW ( 0.000000 0.793103 0.206897 )  
          36) SALES_PRICE < 200950 15   0.00 LOW ( 0.000000 1.000000 0.000000 ) *
          37) SALES_PRICE > 200950 14  19.12 LOW ( 0.000000 0.571429 0.428571 ) *
        19) YEAR_BUILT > 1953.5 35  46.18 MEDIUM ( 0.000000 0.371429 0.628571 ) *
     5) YEAR_BUILT > 1962.5 69  92.84 MEDIUM ( 0.014493 0.289855 0.695652 )  
      10) FINISHED_AREA < 1634 15  15.01 LOW ( 0.000000 0.800000 0.200000 ) *
      11) FINISHED_AREA > 1634 54  54.94 MEDIUM ( 0.018519 0.148148 0.833333 ) *
   3) BATHROOMS > 2.5 279 369.10 MEDIUM ( 0.240143 0.025090 0.734767 )  
     6) SALES_PRICE < 478500 224 186.40 MEDIUM ( 0.080357 0.031250 0.888393 )  
      12) SALES_PRICE < 324450 144  49.88 MEDIUM ( 0.000000 0.041667 0.958333 )  
        24) SALES_PRICE < 192500 12  16.30 MEDIUM ( 0.000000 0.416667 0.583333 ) *
        25) SALES_PRICE > 192500 132  11.76 MEDIUM ( 0.000000 0.007576 0.992424 ) *
      13) SALES_PRICE > 324450 80  95.54 MEDIUM ( 0.225000 0.012500 0.762500 ) *
     7) SALES_PRICE > 478500 55  37.91 HIGH ( 0.890909 0.000000 0.109091 ) *
    Show code
    # View(tr$frame)
    • This tree has one pure node. Which one?

You can see the summary of the tree model with summary()

  • It shows the variables actually used, the residual mean deviance and the Misclassification error rate.
Show code
summary(tr)

Classification tree:
tree(formula = as.factor(QUALITY) ~ . - ID, data = homes)
Variables actually used in tree construction:
[1] "BATHROOMS"     "YEAR_BUILT"    "FINISHED_AREA" "SALES_PRICE"  
Number of terminal nodes:  10 
Residual mean deviance:  0.7013 = 359.1 / 512 
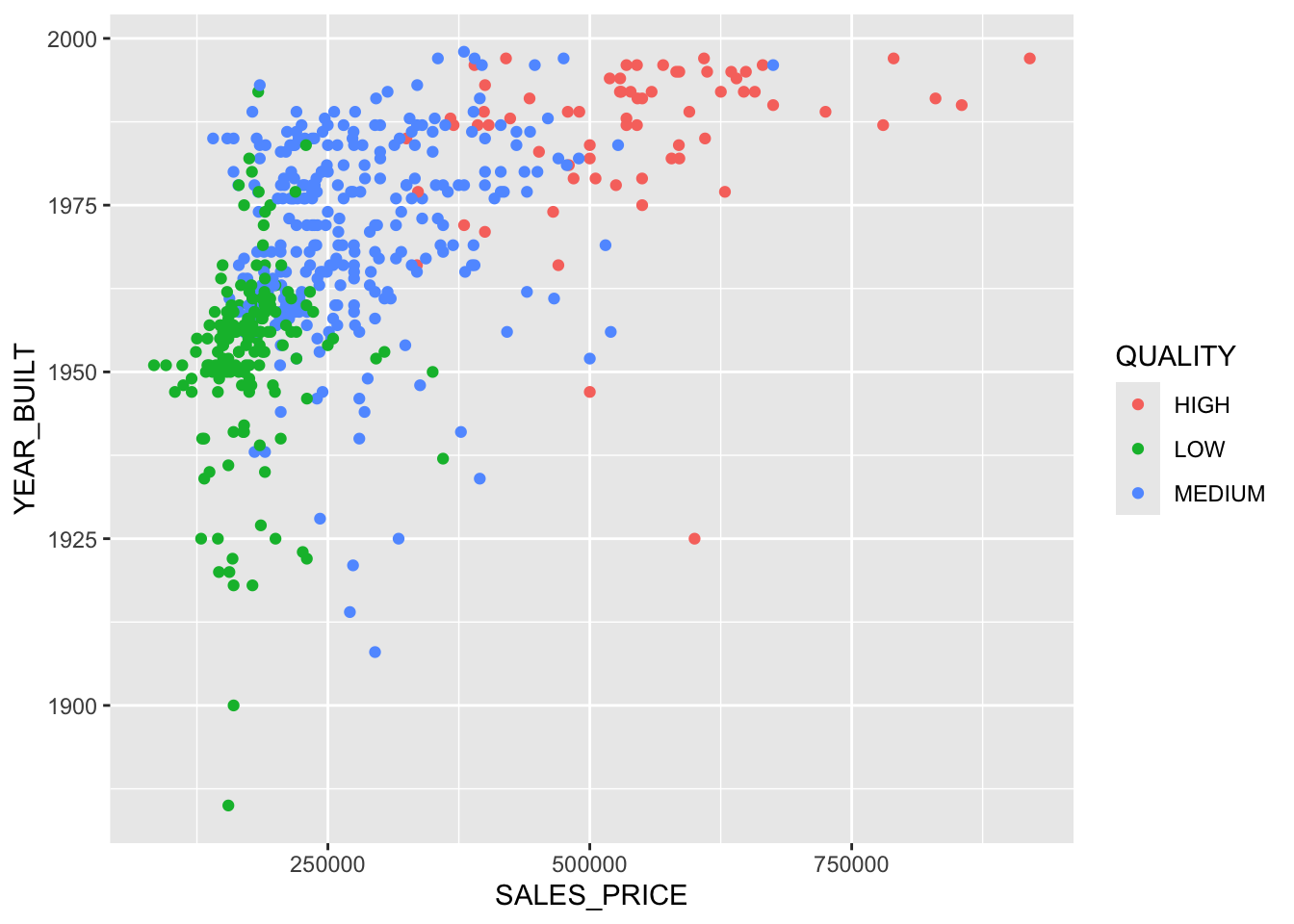
Misclassification error rate: 0.136 = 71 / 522

We can plot the tree results for the two variables.

Show code
ggplot(homes, aes(BATHROOMS, YEAR_BUILT, color = QUALITY)) +
  geom_jitter()

For two other variables.

Show code
ggplot(homes, aes(SALES_PRICE, YEAR_BUILT, color = QUALITY)) +
  geom_point()

Let’s fit a tree with just these two variables.

Show code
tr2 <- tree(as.factor(QUALITY) ~ SALES_PRICE + YEAR_BUILT, data = homes)
plot(tr2)
text(tr2)

Show code
tr2
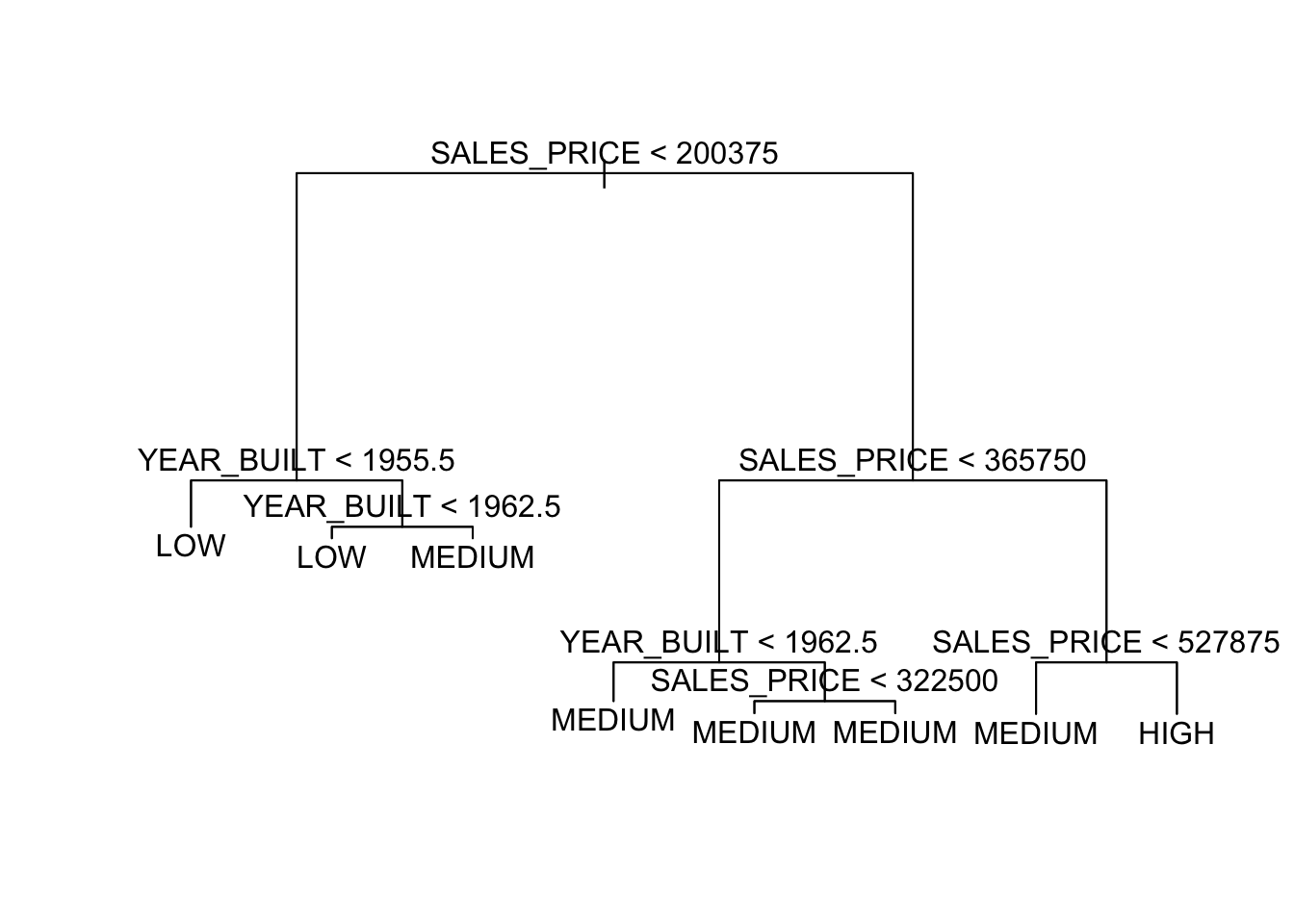
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 522 997.900 MEDIUM ( 0.13027 0.31418 0.55556 )  
   2) SALES_PRICE < 200375 193 224.900 LOW ( 0.00000 0.73057 0.26943 )  
     4) YEAR_BUILT < 1955.5 78  25.430 LOW ( 0.00000 0.96154 0.03846 ) *
     5) YEAR_BUILT > 1955.5 115 156.900 LOW ( 0.00000 0.57391 0.42609 )  
      10) YEAR_BUILT < 1962.5 69  84.800 LOW ( 0.00000 0.69565 0.30435 ) *
      11) YEAR_BUILT > 1962.5 46  61.580 MEDIUM ( 0.00000 0.39130 0.60870 ) *
   3) SALES_PRICE > 200375 329 490.900 MEDIUM ( 0.20669 0.06991 0.72340 )  
     6) SALES_PRICE < 365750 221 178.700 MEDIUM ( 0.01357 0.10407 0.88235 )  
      12) YEAR_BUILT < 1962.5 71  84.430 MEDIUM ( 0.00000 0.28169 0.71831 ) *
      13) YEAR_BUILT > 1962.5 150  58.700 MEDIUM ( 0.02000 0.02000 0.96000 )  
        26) SALES_PRICE < 322500 120  28.060 MEDIUM ( 0.00000 0.02500 0.97500 ) *
        27) SALES_PRICE > 322500 30  19.500 MEDIUM ( 0.10000 0.00000 0.90000 ) *
     7) SALES_PRICE > 365750 108 145.200 HIGH ( 0.60185 0.00000 0.39815 )  
      14) SALES_PRICE < 527875 67  88.520 MEDIUM ( 0.37313 0.00000 0.62687 ) *
      15) SALES_PRICE > 527875 41   9.403 HIGH ( 0.97561 0.00000 0.02439 ) *

Now we can see how the splits are separating the space.

Show code
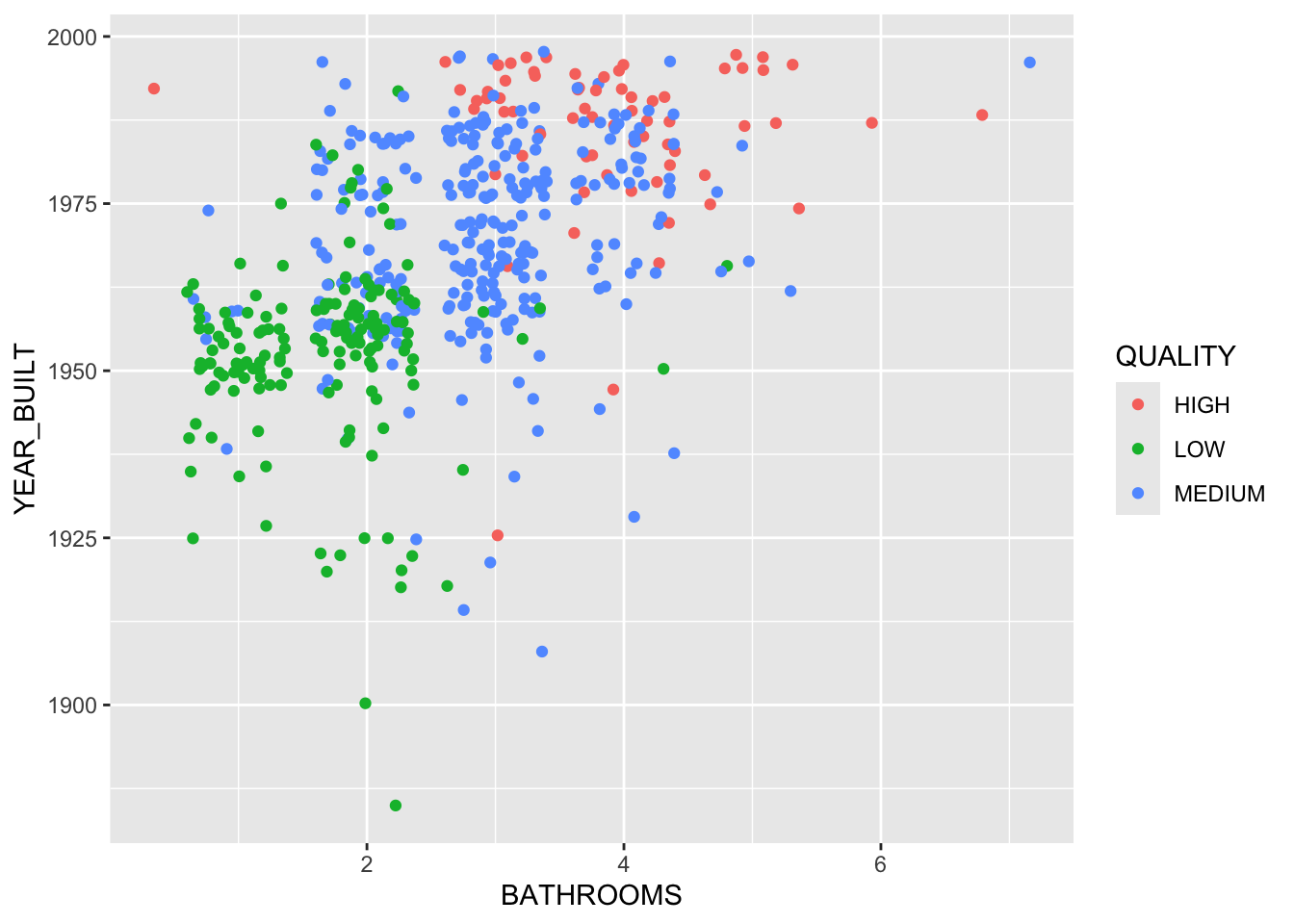
ggplot(homes, aes(SALES_PRICE, YEAR_BUILT, color = QUALITY)) +
  geom_point() +
  geom_vline(xintercept = 200375, lty = 1, color = "red",
             linewidth = 2, alpha = .4) +
  geom_vline(xintercept = 365750, lty = 2, color = "brown", linewidth = 1) +
  geom_line(data = data.frame(x = c(0, 200375), y = c(1955.5, 1955.5)),
            aes(x, y), color = "brown", lty = 2, linewidth = 1)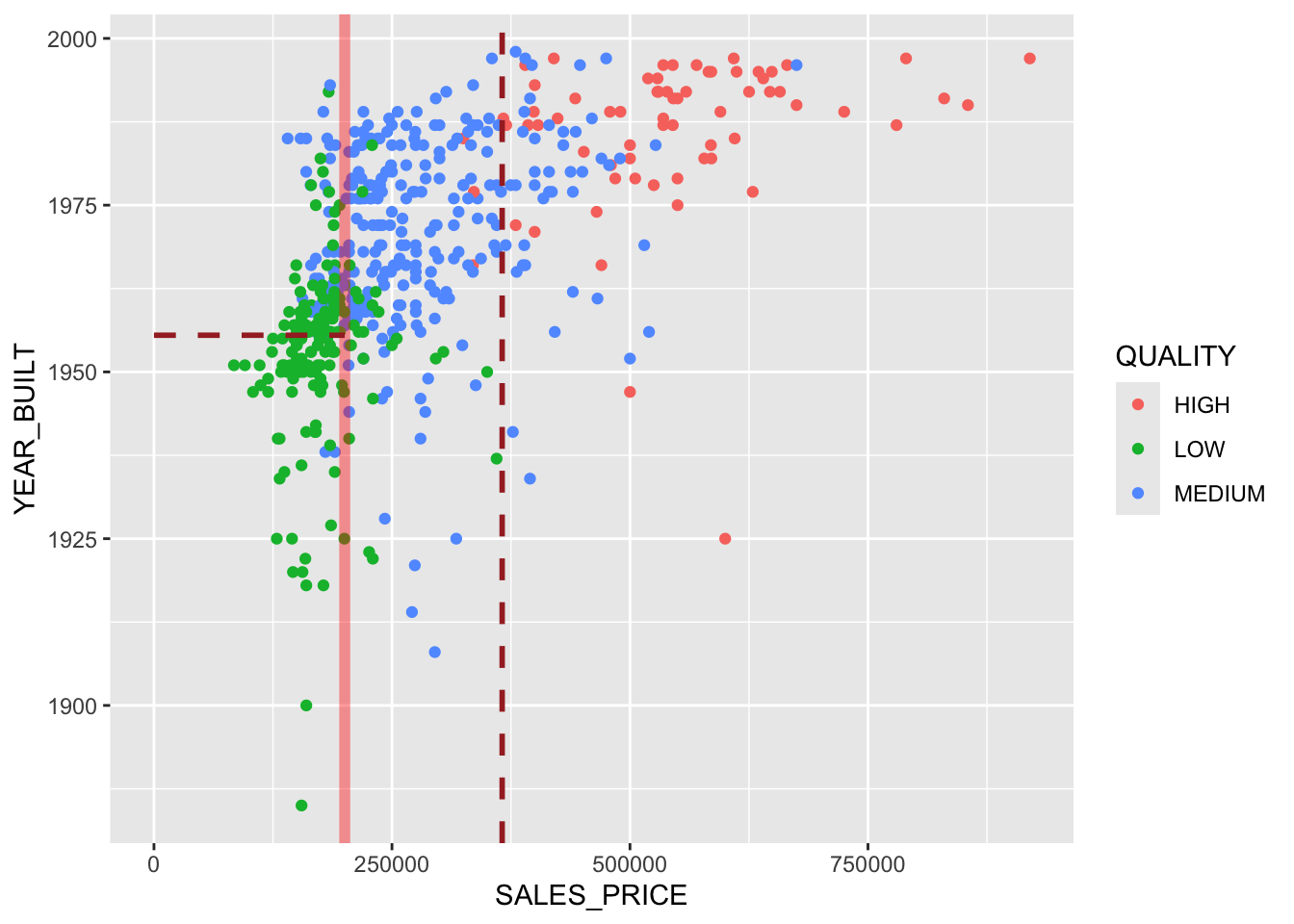

You can see the whole layout with Base R plots and tree::partition.tree().

Show code
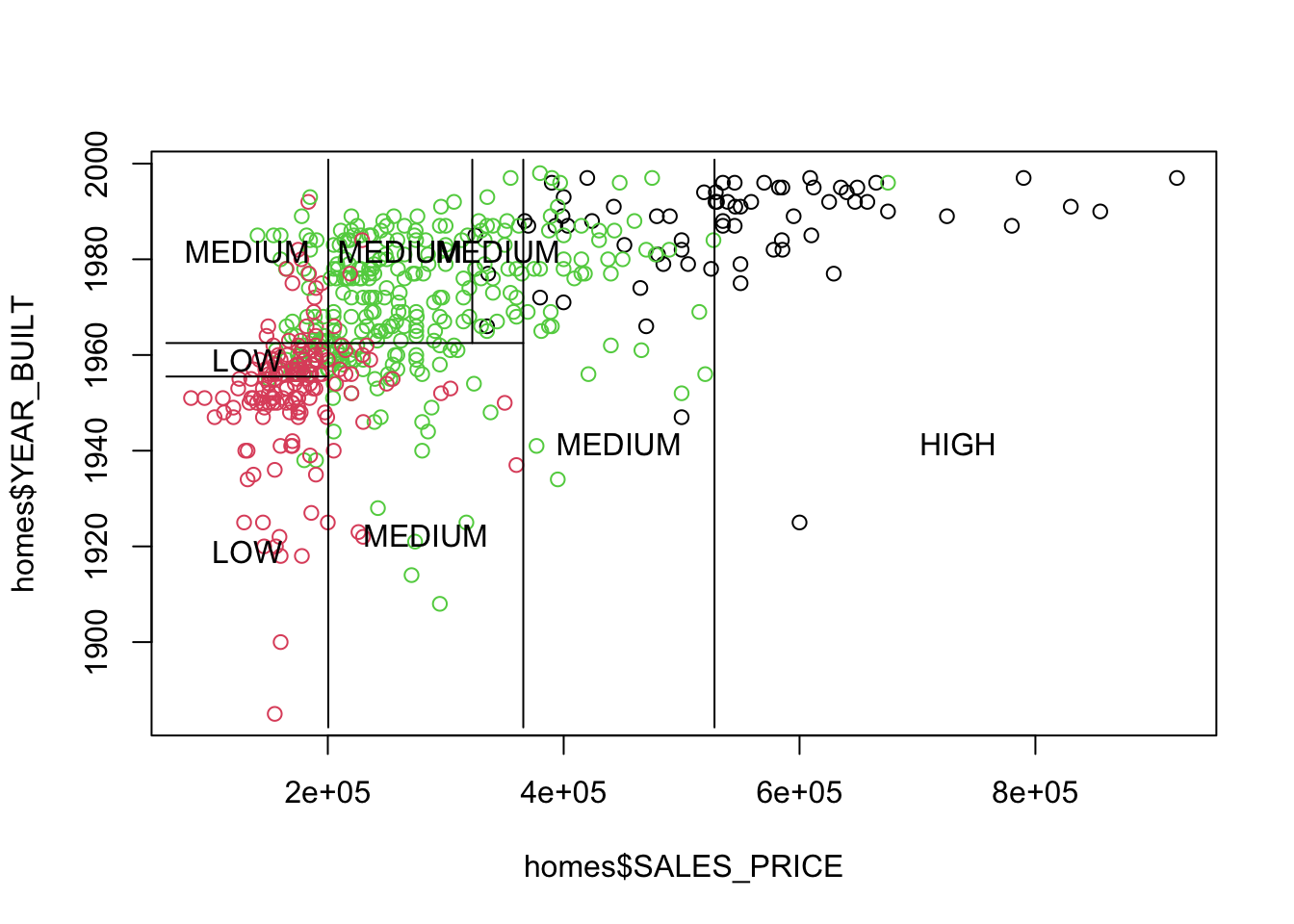
plot(homes$SALES_PRICE, homes$YEAR_BUILT, col = as.factor(homes$QUALITY)) 
partition.tree(tr2, add = TRUE)

Each rectangle corresponds to a terminal node.

Important

Both representations of the two-variable tree in Figure 8.2 have equal information.

  • You can translate from one to the other or create one from the other.
  • You can create trees with more than two predictor variables but you cannot plot them as easily.
Show code
par(mfrow = c(2, 1), mar = c(4, 3, 0.8, 0.4))
plot(tr2, type = "uniform")
text(tr2)
plot(homes$SALES_PRICE, homes$YEAR_BUILT, col = as.factor(homes$QUALITY)) 
partition.tree(tr2, add = TRUE)
Figure 8.2: Two equivalent representations of a two predictor classification tree.

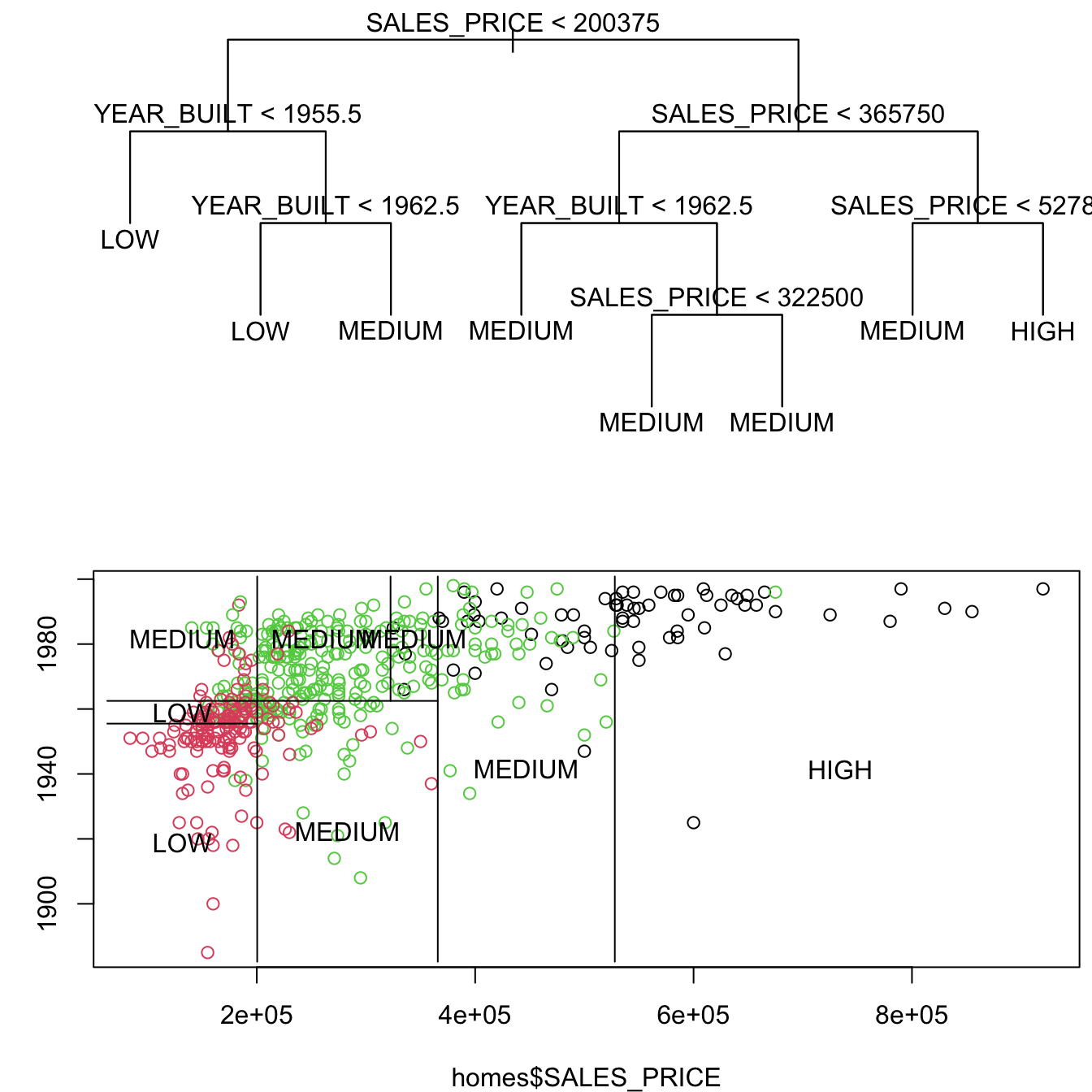
It is straightforward to go from the tree diagram to the plot.

  • Start at the top and draw a line matching the variable and threshold of the split.
  • Move to the next level and repeat for each branch.
  • When you get to a leaf node, label the cell based on the prediction.

It can be more challenging to go from the plot back to the tree as the root may not be obvious at first.

  • You can see the variables and thresholds.

  • It is a process of clearly identifying the thresholds along with the lesser-included conditions.

  • Look for the most common variable and threshold combinations and work down each branch.

  • Label each cell and identify the variables and conditions and decisions. (numbers reduced in digits in what follows)

    1.  sp \< 2 and yb \> 55 and yb \> 62 = M
2.  sp \< 2 and yb \< 55 and yb \< 62 = L
3.  sp \< 2 and yb \< 55 = L
4.  sp \> 2 and sp \< 3.6 and sp \< 3.2 and yb \> 62 = M
5.  sp \> 2 and sp \< 3.6 and sp \< 3.2 and yb \> 62 = M
6.  sp \> 2 and sp \< 3.6 and yb \< 62 = M
7.  sp \> 2 and sp \> 3.6 and sp \< 5.5 = M
8.  sp \> 2 and sp \> 3.6 and sp \> 5.5 = H

  • 8 cells means 7 splits.

  • Reorder them if necessary and look for the most common variable/threshold (with lesser included cases).

    • Here we can see SALES_PRICE < 2 is the root node as it occurs in every case.

  • For those that are TRUE, go fown that branch and look for the next most common (with lesser included cases).

    • Consider YEAR_BUILT < 55 as the node since 55 < 65.

  • Keep working down the branch for cases (1, 2, 3).

    • Left side (3): True means Leaf node for Low
    • Right side (1, 2): Consider yb < 62, then, not a leaf node, so consider
      • Left side (2): True means Leaf node for Low
      • Right Side (1): True means Leaf node for Medium.

  • That completes cases 1, 2, and 3.

  • Go back to the root node and start working the next layer considering only those decisions not yet mapped out (4, 5, 6, 7, 8).

  • Look for most common variable/threshold (with lesser included cases).

  • Consider SALES_PRCE < 3.6. It has three true and two false.

    • Left side:YB < 62 most common as next split
      • Left: Leaf -> Medium
      • Right: SP < 3.2
        • Left: Leaf -> Medium
        • Right: Leaf -> Medium
      • That completes 4, 5, 6.
    • Right side: sp < 5.5
      • Left Leaf -> Medium
      • Right Leaf - High
      • That completes 7, 8.

  • All splits are now completed.

8.4.4 Tuning the Tree

The algorithm decides what splits to make to maximize the reduction in MSE or the gini impurity index.

We can tune the tree based on how many terminal nodes we want it to have.

We can use cross-validation with a validation set to assess performance.

  • cv.tree() runs \(K\)-fold cross validation with \(K=10\).
  • When fitting the trees, it also calls prune.tree() which will trim leaves by recursively “snipping” off the least important splits.
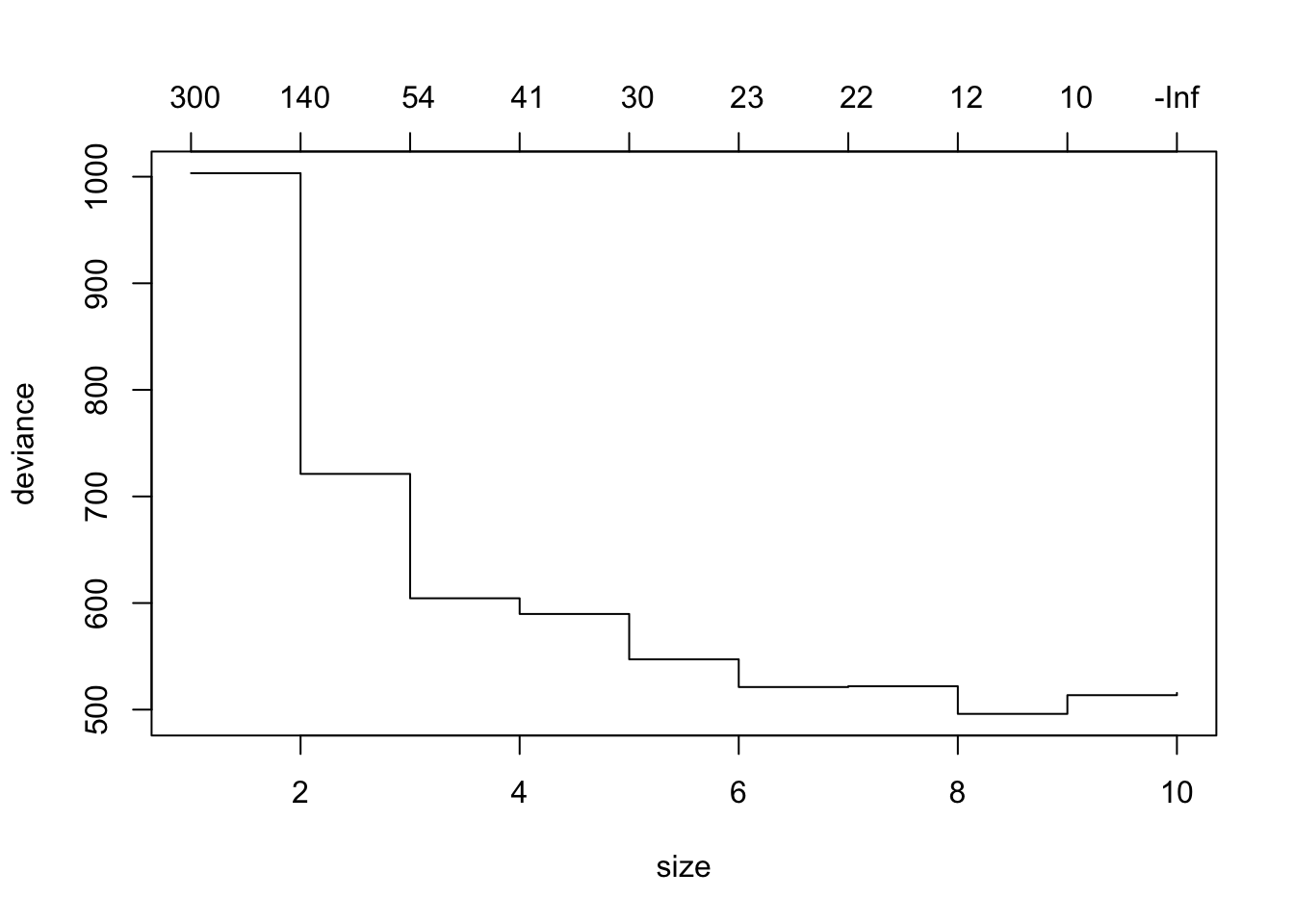
Show code
tr <- tree::tree(as.factor(QUALITY) ~ . - ID, data = homes)
set.seed(1234)
cv <- cv.tree(tr)
cv
$size
 [1] 10  9  8  7  6  5  4  3  2  1

$dev
 [1]  515.6691  513.5611  496.0108  521.9305  521.1874  547.1770  589.7400
 [8]  604.4614  721.1613 1003.3119

$k
 [1]      -Inf  10.44788  11.97109  21.82445  22.89045  30.04703  40.95862
 [8]  53.80531 144.81740 302.03830

$method
[1] "deviance"

attr(,"class")
[1] "prune"         "tree.sequence"
  • size is the number of terminal nodes in the tree (in decreasing order left to right).
  • dev is the measure of log-likelihood and the lowest number is the best fit. Here that is 8 terminal nodes at 496.
  • k is the value of the cost-complexity parameter used by prune.tree() to prune the tree.
    • This is a tuning parameter of a penalty function used to drive down the number of terminal nodes based on the overall performance of the tree (misclassification rate) and reduce overfitting.
    • Similar in concept to \(\lambda\) used in shrinkage methods or adjusted R2 in regression.
    • Without it the tree would grow larger and larger while overfitting.

Our initial tree had 10 nodes so the cross validation will only address the nodes in the original tree and fewer.

You can get the tree size with the minimum deviance and also plot the cross validation results.

  • The numbers across the top are the values of \(k\), the cost complexity parameter, and -Inf is the default for getting the largest tree possible - with the greatest chance of overfitting.
Show code
cv$size[which.min(cv$dev)]
[1] 8
Show code
plot(cv)

To see the new, optimal, tree, use prune.tree() with the best number of nodes.

Show code
tr_opt <- prune.tree(tr, best = 8)
summary(tr_opt)

Classification tree:
snip.tree(tree = tr, nodes = 9L)
Variables actually used in tree construction:
[1] "BATHROOMS"     "YEAR_BUILT"    "FINISHED_AREA" "SALES_PRICE"  
Number of terminal nodes:  8 
Residual mean deviance:  0.7422 = 381.5 / 514 
Misclassification error rate: 0.1533 = 80 / 522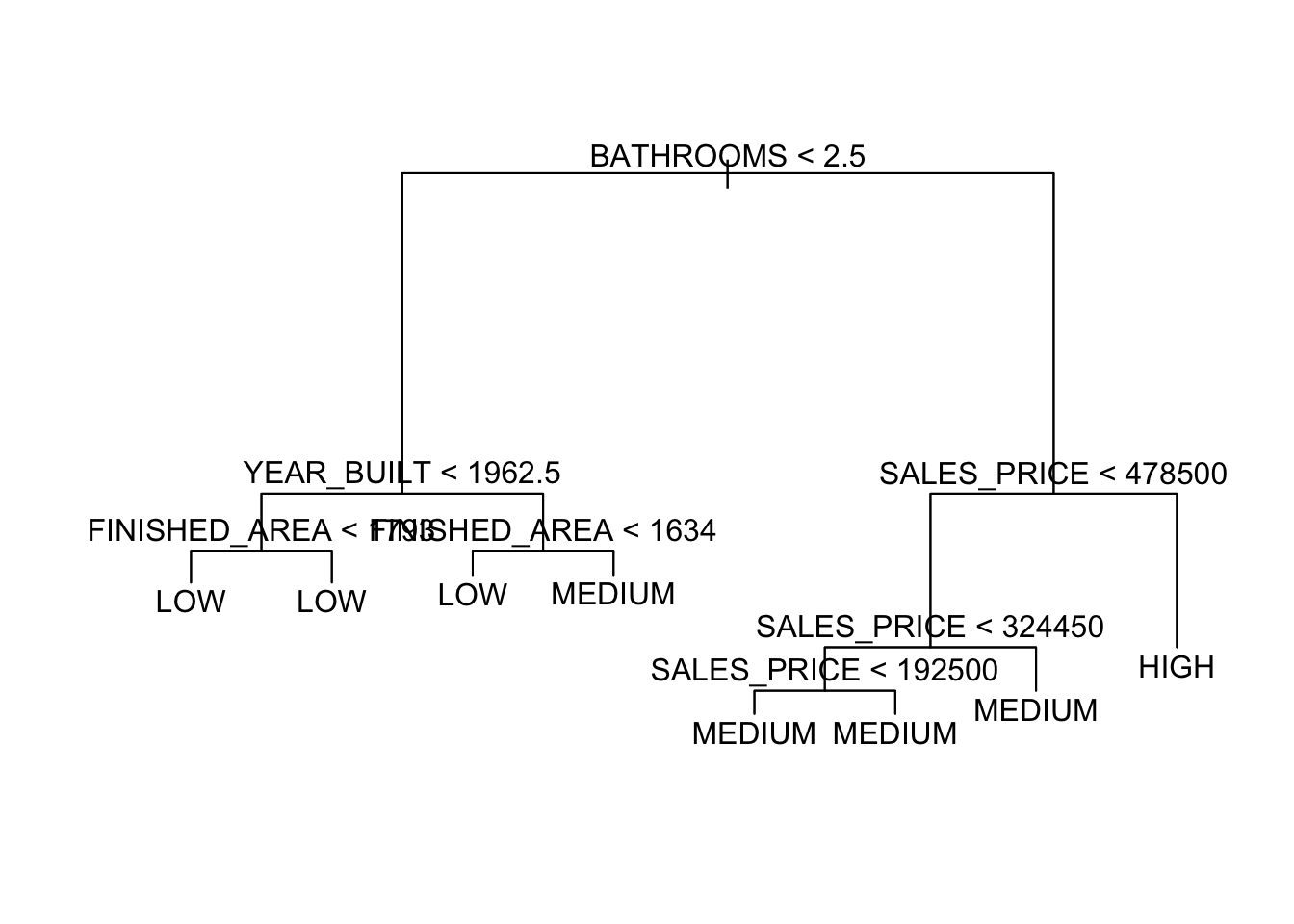
Show code
plot(tr_opt)
text(tr_opt)

This optimum is based on deviance for regression and classification trees.

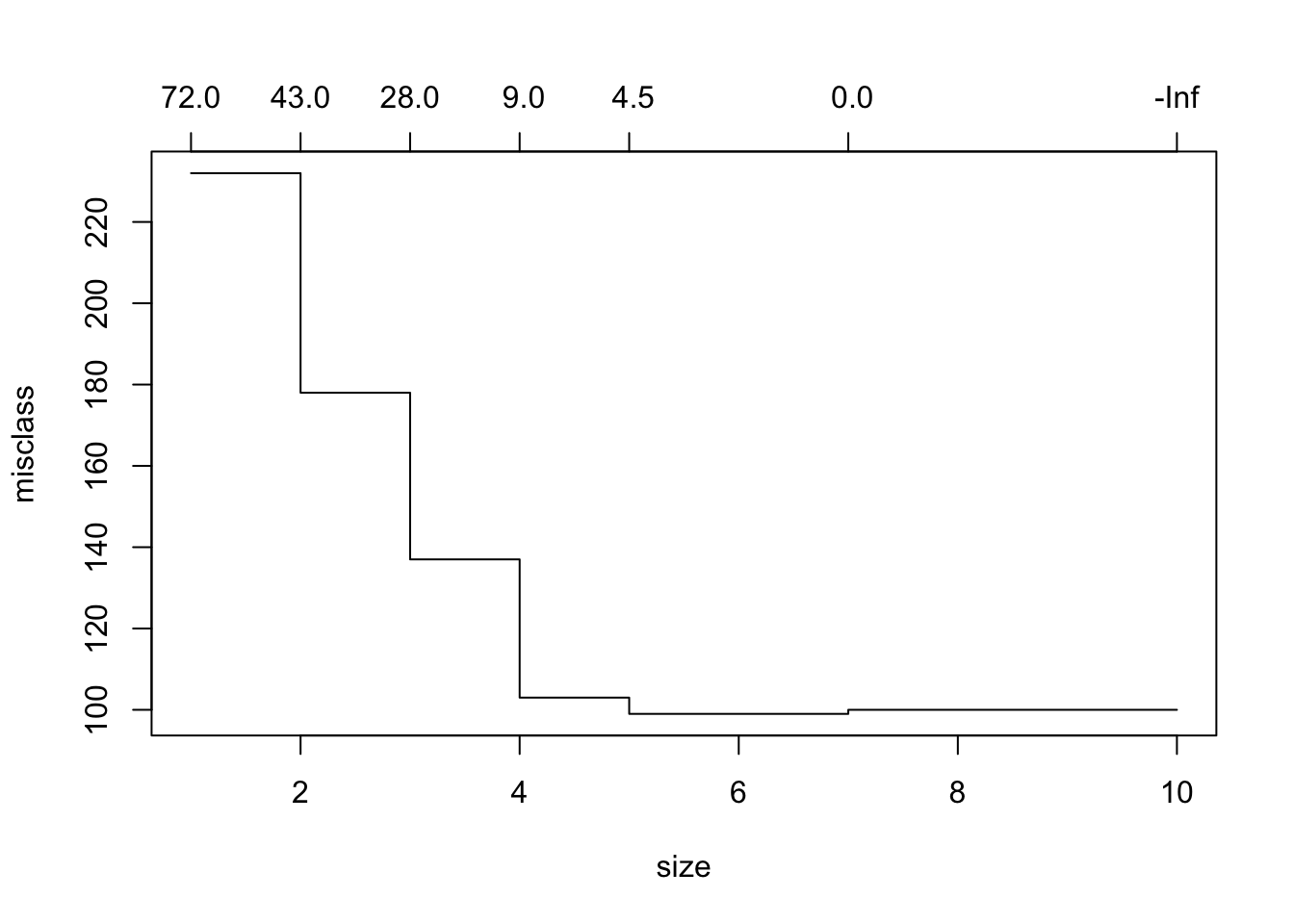
For classification trees only, we can choose to prune based on the misclassification rate.

Show code
cv_m <- cv.tree(tr, FUN = prune.misclass)
cv_m
$size
[1] 10  7  5  4  3  2  1

$dev
[1] 100 100  99 103 137 178 232

$k
[1] -Inf  0.0  4.5  9.0 28.0 43.0 72.0

$method
[1] "misclass"

attr(,"class")
[1] "prune"         "tree.sequence"
  • Here dev is not deviance but the number of misclassified responses.
Show code
plot(cv_m)

Here it says to use 5 branches.

Show code
tr_opt_m <- prune.misclass(tr, best = 5)
plot(tr_opt_m)
text(tr_opt_m)

8.4.5 Regression Trees in R

Let’s predict SALES_PRICE.

Show code
tr <- tree::tree(SALES_PRICE ~ . -ID - QUALITY + as.factor(QUALITY), 
                 data = homes)
tr
node), split, n, deviance, yval
      * denotes terminal node

 1) root 522 9.911e+12 277900  
   2) as.factor(QUALITY): LOW,MEDIUM 454 3.360e+12 238100  
     4) FINISHED_AREA < 2223.5 307 7.316e+11 196900  
       8) BATHROOMS < 2.5 223 2.850e+11 180500 *
       9) BATHROOMS > 2.5 84 2.279e+11 240300 *
     5) FINISHED_AREA > 2223.5 147 1.016e+12 324200  
      10) FINISHED_AREA < 2818.5 96 3.261e+11 286600 *
      11) FINISHED_AREA > 2818.5 51 2.982e+11 395000 *
   3) as.factor(QUALITY): HIGH 68 1.031e+12 543600  
     6) FINISHED_AREA < 3846.5 52 4.568e+11 513600 *
     7) FINISHED_AREA > 3846.5 16 3.742e+11 641300  
      14) YEAR_BUILT < 1989.5 7 9.193e+10 524800 *
      15) YEAR_BUILT > 1989.5 9 1.135e+11 731900 *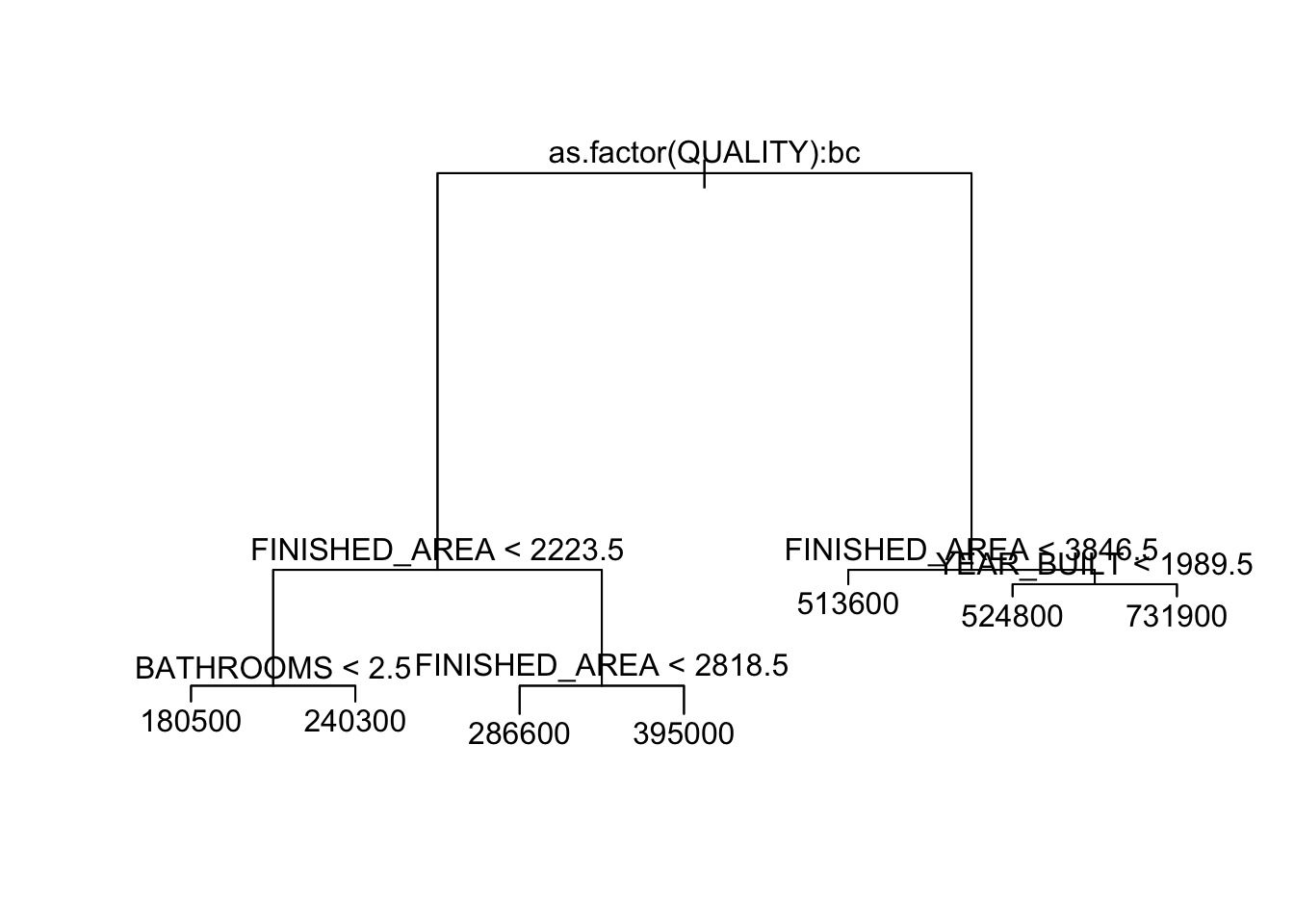
Show code
plot(tr)
text(tr)

Show code
as.factor(homes$QUALITY) |> levels()
[1] "HIGH"   "LOW"    "MEDIUM"

The terminal nodes each have a \(\hat{y}_m=\bar{y}_m\) as the mean of the price of the houses that were left in the \(m\)th node.

  • The root node splits on a categorical variable QUALITY.
    • The bc means that to the left (YES) are the second and third levels of the QUALITY variable (MEDIUM and LOW). and HIGH is to the right (NO).
  • Note that it always adds .5 to avoid ties.
  • As before, the values in the output for \(k\) and on the top of the plot are the values of the cost complexity parameter, not the cross-fold validation \(K\).
Show code
cv <- cv.tree(tr)
cv
$size
[1] 7 6 5 4 3 2 1

$dev
[1] 2.501469e+12 2.455349e+12 2.665192e+12 2.710722e+12 2.907232e+12
[6] 4.480617e+12 9.947553e+12

$k
[1]         -Inf 1.687930e+11 1.996989e+11 2.186610e+11 3.914207e+11
[6] 1.612596e+12 5.520274e+12

$method
[1] "deviance"

attr(,"class")
[1] "prune"         "tree.sequence"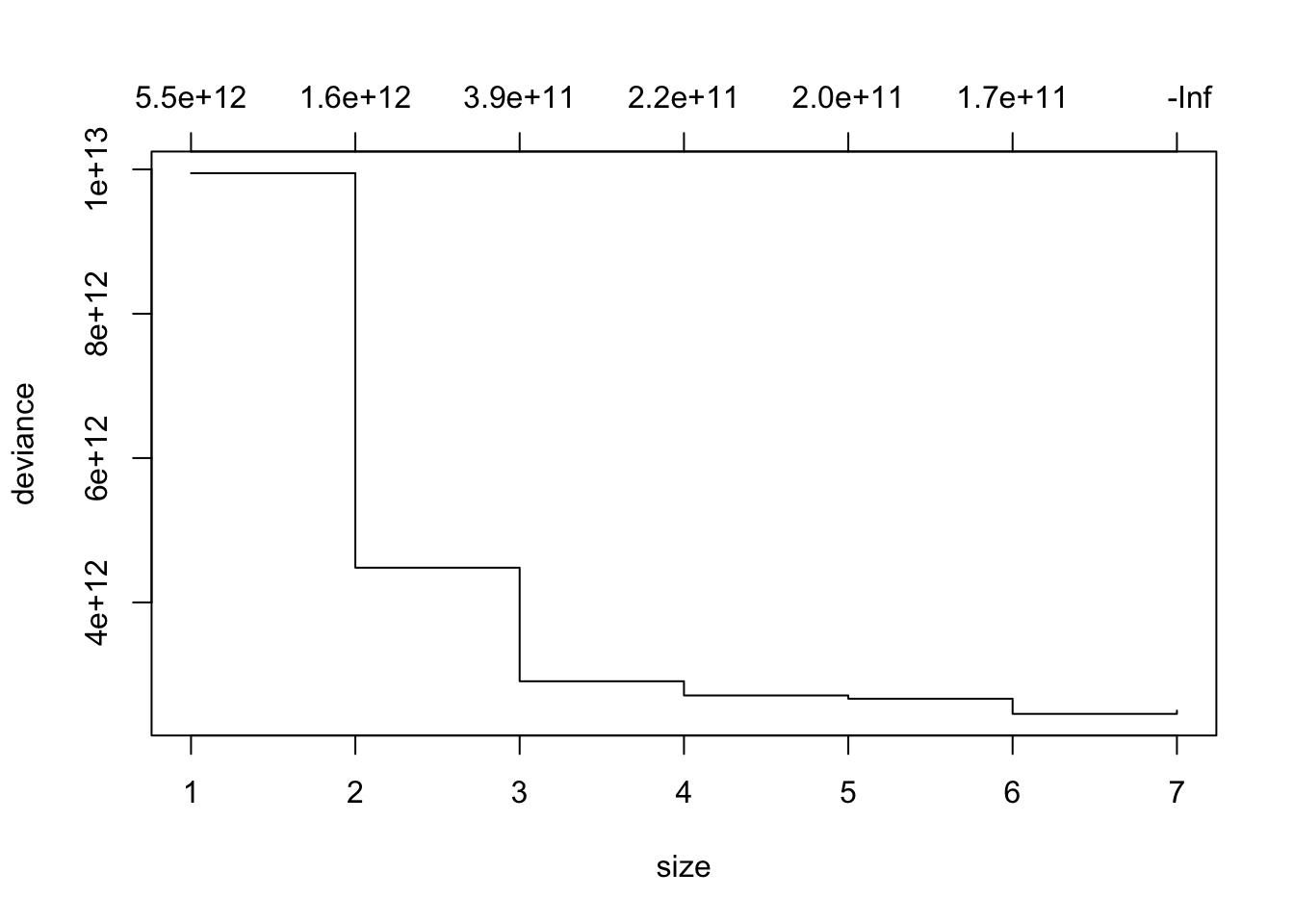
Show code
plot(cv)

To assess accuracy we will grow many trees and use bootstrap to assess.

  • We will look at Bagging (bootstrap aggregation) and then use random selection to minimize correlation (random forests).

8.5 Trees vs. Regression

Regression: \(Y = \beta_0 + \beta_1 X_1 + \cdots\)

Trees: \(Y = \beta_1 I_{A_1} + \beta_2 I_{A_2}\cdots\) splits the \(X\) into regions \(A_j\).

Regression and Trees all fall into the set of base functions we could use for the splines.

If your data looks like the following, regression works well to separate.

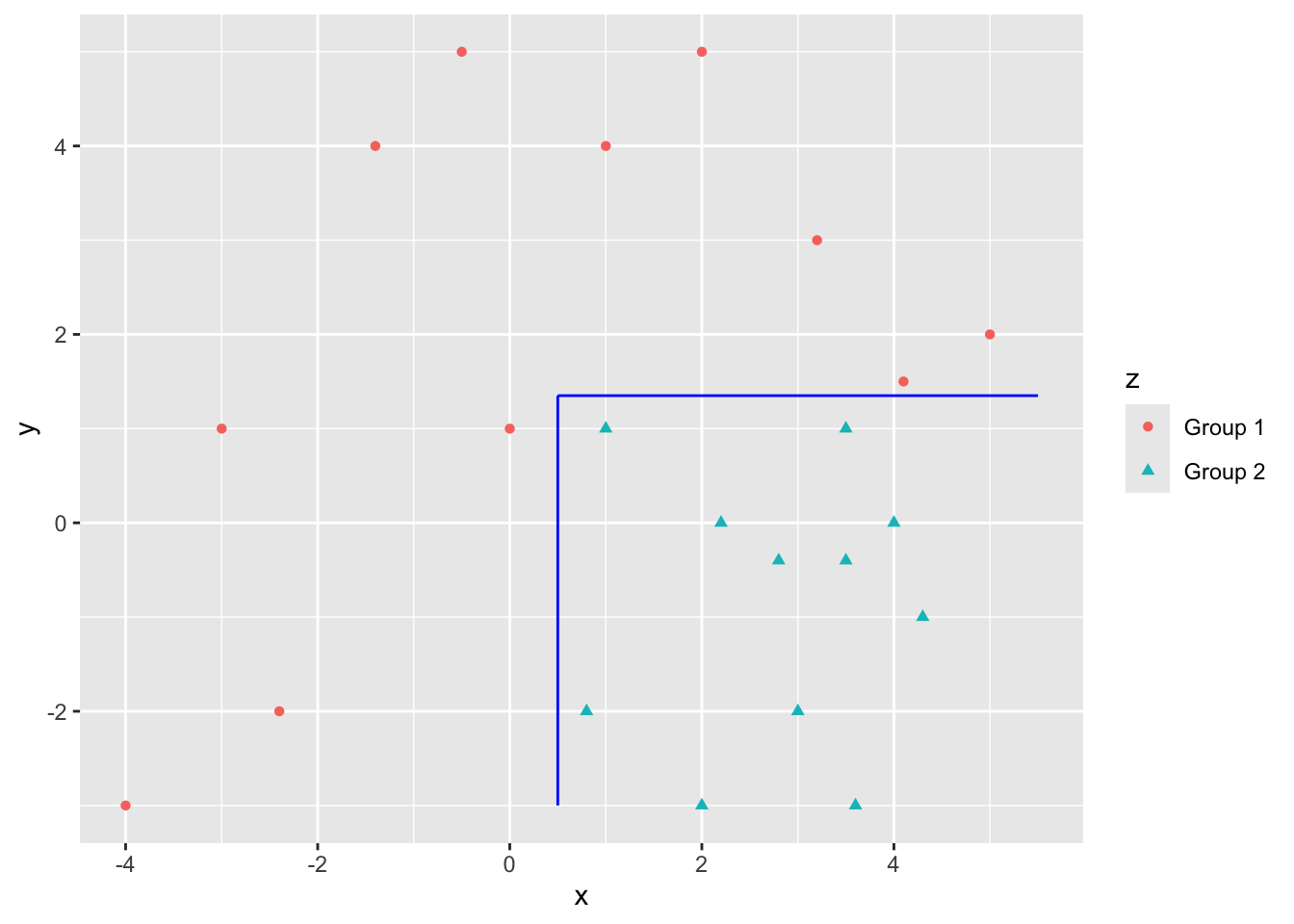
If your data looks like this, regression does not do as well.

  • But trees can split the data nicely for a good fit

8.6 Example: Titanic Data

Let’s load the {DALEX} titanic data set.

Show code
data("titanic", package = "DALEX")
names(titanic)
[1] "gender"   "age"      "class"    "embarked" "country"  "fare"     "sibsp"   
[8] "parch"    "survived"

We predicted survival using other methods. Let’s try a tree.

Show code
library(tree)
Show code
tr <- tree(survived ~ ., data = titanic)
Error in tree(survived ~ ., data = titanic): factor predictors must have at most 32 levels

Let’s check out the source of the error.

Show code
glimpse(titanic)
Rows: 2,207
Columns: 9
$ gender   <fct> male, male, male, female, female, male, male, female, male, m…
$ age      <dbl> 42.0000000, 13.0000000, 16.0000000, 39.0000000, 16.0000000, 2…
$ class    <fct> 3rd, 3rd, 3rd, 3rd, 3rd, 3rd, 2nd, 2nd, 3rd, 3rd, 3rd, 3rd, 3…
$ embarked <fct> Southampton, Southampton, Southampton, Southampton, Southampt…
$ country  <fct> United States, United States, United States, England, Norway,…
$ fare     <dbl> 7.1100, 20.0500, 20.0500, 20.0500, 7.1300, 7.1300, 24.0000, 2…
$ sibsp    <dbl> 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0…
$ parch    <dbl> 0, 2, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0…
$ survived <fct> no, no, no, yes, yes, yes, no, yes, yes, yes, no, no, no, yes…
Show code
levels(titanic$country)
 [1] "Argentina"             "Australia"             "Austria"              
 [4] "Belgium"               "Bosnia"                "Bulgaria"             
 [7] "Canada"                "Channel Islands"       "China/Hong Kong"      
[10] "Croatia"               "Croatia (Modern)"      "Cuba"                 
[13] "Denmark"               "Egypt"                 "England"              
[16] "Finland"               "France"                "Germany"              
[19] "Greece"                "Hungary"               "India"                
[22] "Ireland"               "Italy"                 "Japan"                
[25] "Latvia"                "Lebanon"               "Mexico"               
[28] "Netherlands"           "Northern Ireland"      "Norway"               
[31] "Peru"                  "Poland"                "Russia"               
[34] "Scotland"              "Siam"                  "Slovakia (Modern day)"
[37] "Slovenia"              "South Africa"          "Spain"                
[40] "Sweden"                "Switzerland"           "Syria"                
[43] "Turkey"                "United States"         "Uruguay"              
[46] "Wales"                 "Yugoslavia"            "Guyana"

We can eliminate country from the model and try again.

Let’s use three different approaches to removing country from the model

  • Remove from the model formula.
  • Don’t add into the model.
  • Remove from the data frame.
Show code
tr0 <- tree(survived ~ . - country, data = titanic)

tr <- tree(survived ~ gender + age + class + embarked + fare + sibsp + parch, 
           data = titanic)

titanic2 <- titanic[, !(names(titanic) %in% "country")]
tr2 <- tree(survived ~ ., data = titanic2)
tr0
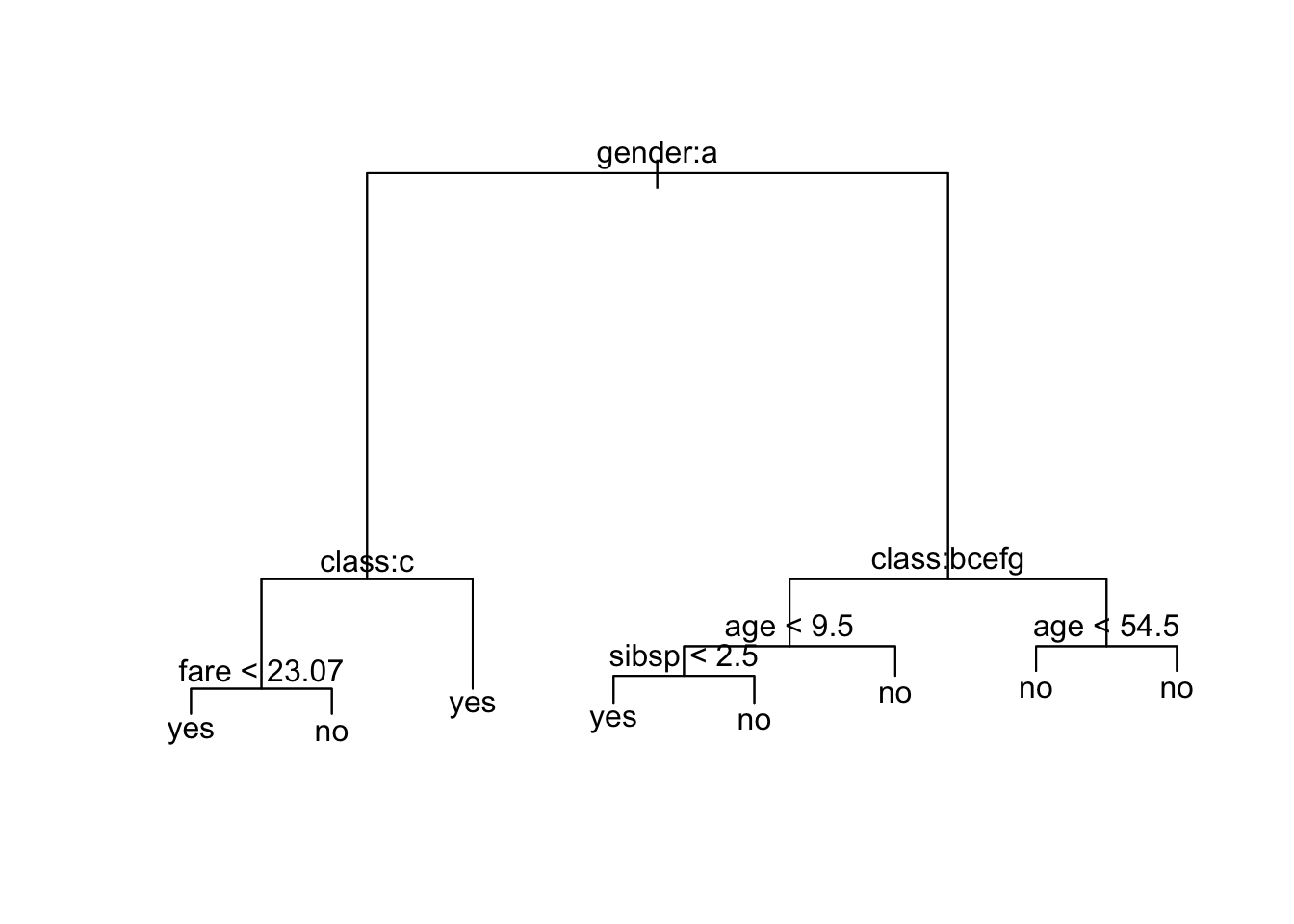
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 2099 2645.000 no ( 0.67556 0.32444 )  
   2) gender: female 464  536.700 yes ( 0.26509 0.73491 )  
     4) class: 3rd 207  287.000 no ( 0.50242 0.49758 ) *
     5) class: 1st,2nd,restaurant staff,victualling crew 257  135.500 yes ( 0.07393 0.92607 ) *
   3) gender: male 1635 1672.000 no ( 0.79205 0.20795 )  
     6) class: 2nd,3rd,engineering crew,restaurant staff,victualling crew 1400 1273.000 no ( 0.83071 0.16929 )  
      12) age < 9.5 44   60.910 yes ( 0.47727 0.52273 )  
        24) sibsp < 2.5 27   25.870 yes ( 0.18519 0.81481 ) *
        25) sibsp > 2.5 17    7.606 no ( 0.94118 0.05882 ) *
      13) age > 9.5 1356 1183.000 no ( 0.84218 0.15782 ) *
     7) class: 1st,deck crew 235  322.200 no ( 0.56170 0.43830 )  
      14) age < 54.5 201  278.600 yes ( 0.49751 0.50249 ) *
      15) age > 54.5 34   15.210 no ( 0.94118 0.05882 ) *
Show code
tr
node), split, n, deviance, yval, (yprob)
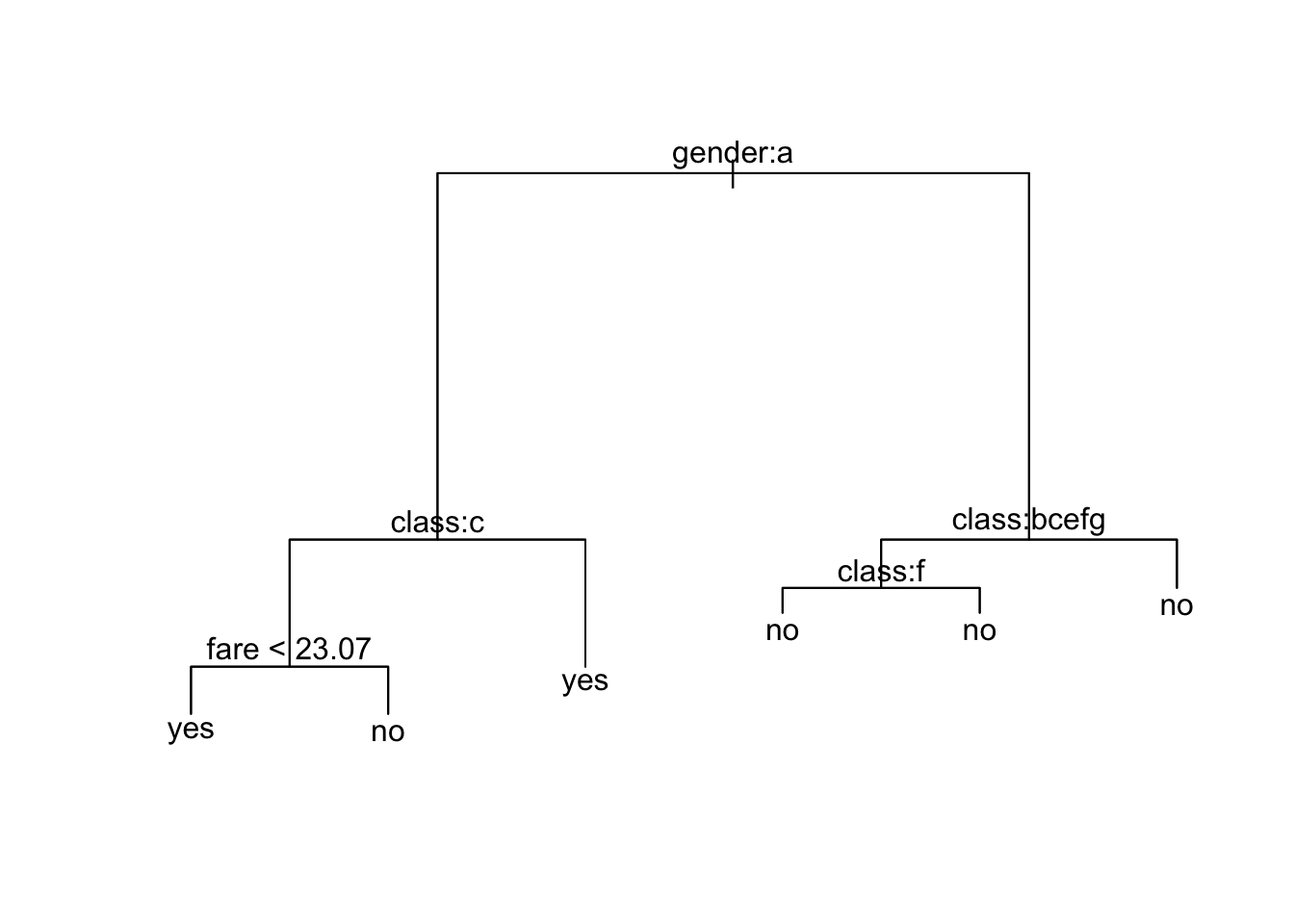
      * denotes terminal node

 1) root 2179 2749.000 no ( 0.67462 0.32538 )  
   2) gender: female 489  566.300 yes ( 0.26585 0.73415 )  
     4) class: 3rd 216  299.400 no ( 0.50926 0.49074 )  
       8) fare < 23.07 183  250.800 yes ( 0.43716 0.56284 ) *
       9) fare > 23.07 33   20.110 no ( 0.90909 0.09091 ) *
     5) class: 1st,2nd,restaurant staff,victualling crew 273  143.000 yes ( 0.07326 0.92674 ) *
   3) gender: male 1690 1724.000 no ( 0.79290 0.20710 )  
     6) class: 2nd,3rd,engineering crew,restaurant staff,victualling crew 1451 1321.000 no ( 0.83046 0.16954 )  
      12) age < 9.5 47   64.960 yes ( 0.46809 0.53191 )  
        24) sibsp < 2.5 29   26.660 yes ( 0.17241 0.82759 ) *
        25) sibsp > 2.5 18    7.724 no ( 0.94444 0.05556 ) *
      13) age > 9.5 1404 1222.000 no ( 0.84259 0.15741 ) *
     7) class: 1st,deck crew 239  327.300 no ( 0.56485 0.43515 )  
      14) age < 54.5 205  284.200 no ( 0.50244 0.49756 ) *
      15) age > 54.5 34   15.210 no ( 0.94118 0.05882 ) *
Show code
tr2
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 2179 2749.000 no ( 0.67462 0.32538 )  
   2) gender: female 489  566.300 yes ( 0.26585 0.73415 )  
     4) class: 3rd 216  299.400 no ( 0.50926 0.49074 )  
       8) fare < 23.07 183  250.800 yes ( 0.43716 0.56284 ) *
       9) fare > 23.07 33   20.110 no ( 0.90909 0.09091 ) *
     5) class: 1st,2nd,restaurant staff,victualling crew 273  143.000 yes ( 0.07326 0.92674 ) *
   3) gender: male 1690 1724.000 no ( 0.79290 0.20710 )  
     6) class: 2nd,3rd,engineering crew,restaurant staff,victualling crew 1451 1321.000 no ( 0.83046 0.16954 )  
      12) age < 9.5 47   64.960 yes ( 0.46809 0.53191 )  
        24) sibsp < 2.5 29   26.660 yes ( 0.17241 0.82759 ) *
        25) sibsp > 2.5 18    7.724 no ( 0.94444 0.05556 ) *
      13) age > 9.5 1404 1222.000 no ( 0.84259 0.15741 ) *
     7) class: 1st,deck crew 239  327.300 no ( 0.56485 0.43515 )  
      14) age < 54.5 205  284.200 no ( 0.50244 0.49756 ) *
      15) age > 54.5 34   15.210 no ( 0.94118 0.05882 ) *

What do you notice?

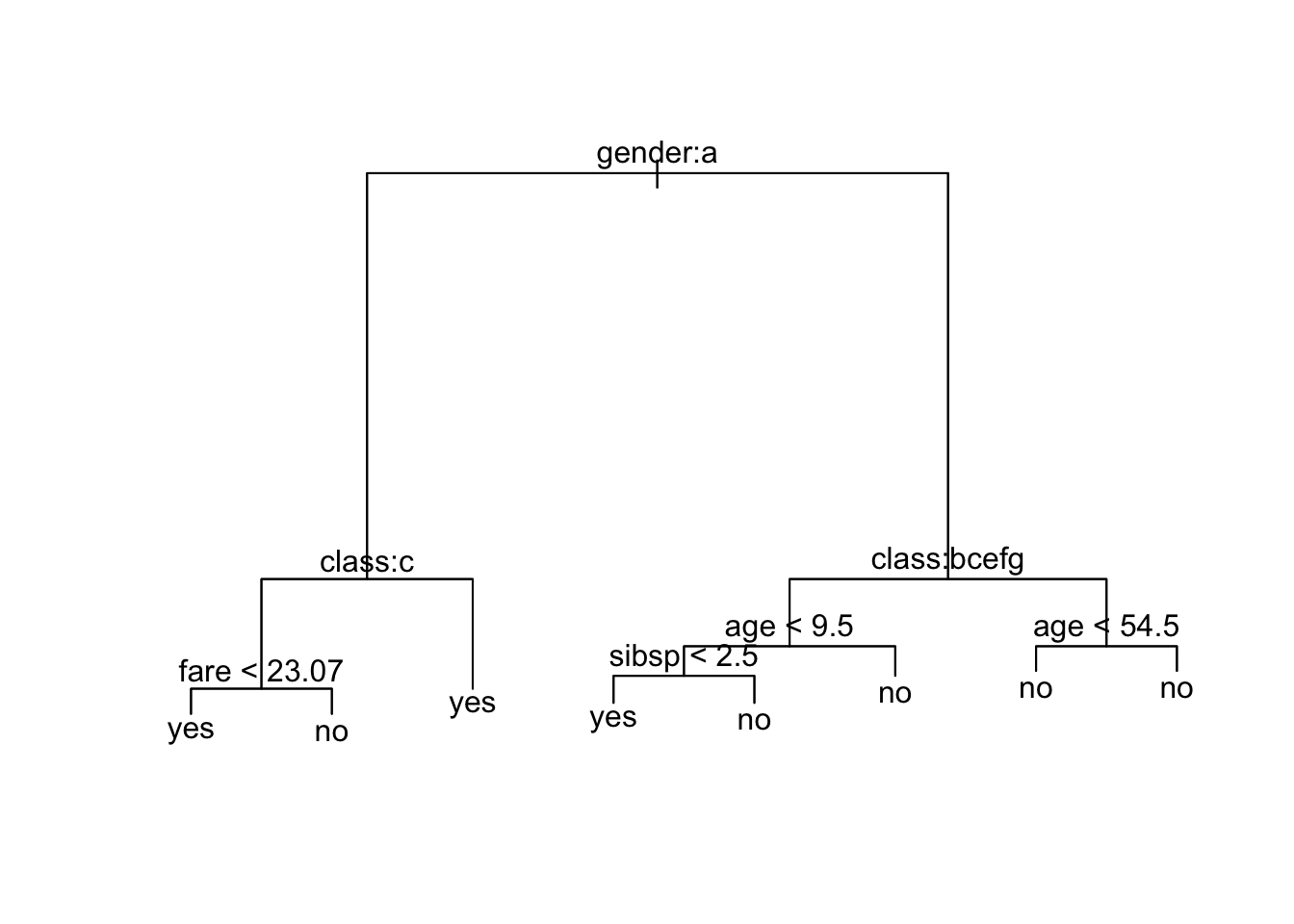
Let’s plot the trees - What do you notice?

Show code
plot(tr0)
text(tr0)
plot(tr)
text(tr)

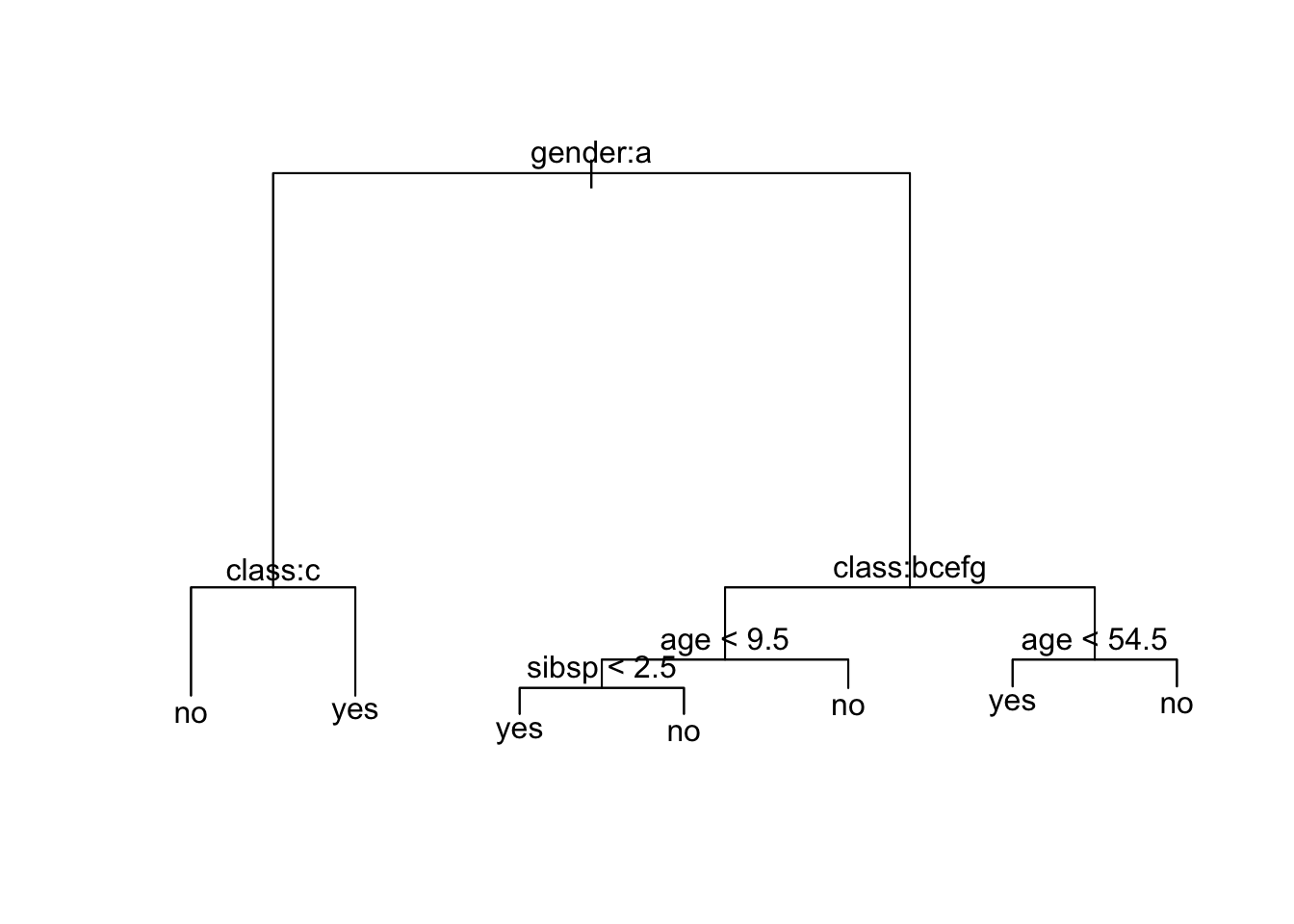
What is going on?

Show code
summary(titanic)
    gender          age                       class            embarked   
 female: 489   Min.   : 0.1667   1st             :324   Belfast    : 197  
 male  :1718   1st Qu.:22.0000   2nd             :284   Cherbourg  : 271  
               Median :29.0000   3rd             :709   Queenstown : 123  
               Mean   :30.4367   deck crew       : 66   Southampton:1616  
               3rd Qu.:38.0000   engineering crew:324                     
               Max.   :74.0000   restaurant staff: 69                     
               NA's   :2         victualling crew:431                     
          country          fare             sibsp            parch       
 England      :1125   Min.   :  0.000   Min.   :0.0000   Min.   :0.0000  
 United States: 264   1st Qu.:  0.000   1st Qu.:0.0000   1st Qu.:0.0000  
 Ireland      : 137   Median :  7.151   Median :0.0000   Median :0.0000  
 Sweden       : 105   Mean   : 19.773   Mean   :0.2972   Mean   :0.2294  
 Lebanon      :  71   3rd Qu.: 20.111   3rd Qu.:0.0000   3rd Qu.:0.0000  
 (Other)      : 424   Max.   :512.061   Max.   :8.0000   Max.   :9.0000  
 NA's         :  81   NA's   :26        NA's   :10       NA's   :10      
 survived  
 no :1496  
 yes: 711

Note the number of NAs in country.

Show code
nrow(titanic) - (titanic[,-5] |> 
  rowwise()  |> 
  mutate(sum_na  = sum(across(everything(), is.na))) |> 
    ungroup() |> 
  filter(sum_na > 0) |> 
  nrow())
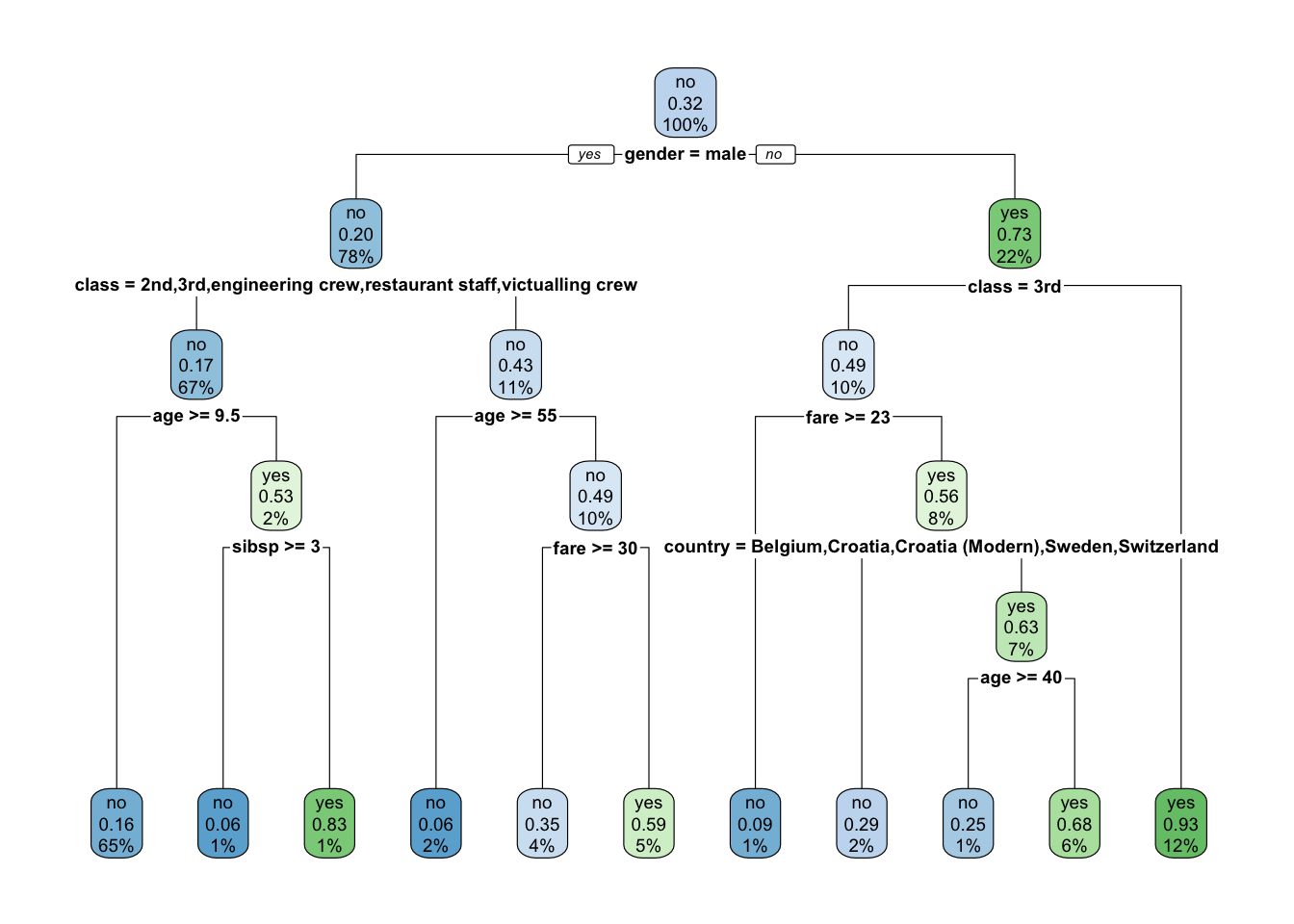
[1] 2179

Let’s use the tree model with the most data (the 80 extra rows of data).

Show code
plot(tr)
text(tr)

Recall the height of the line for each split is proportional to the amount of SSE (regression) or deviance (classification) explained by the split.

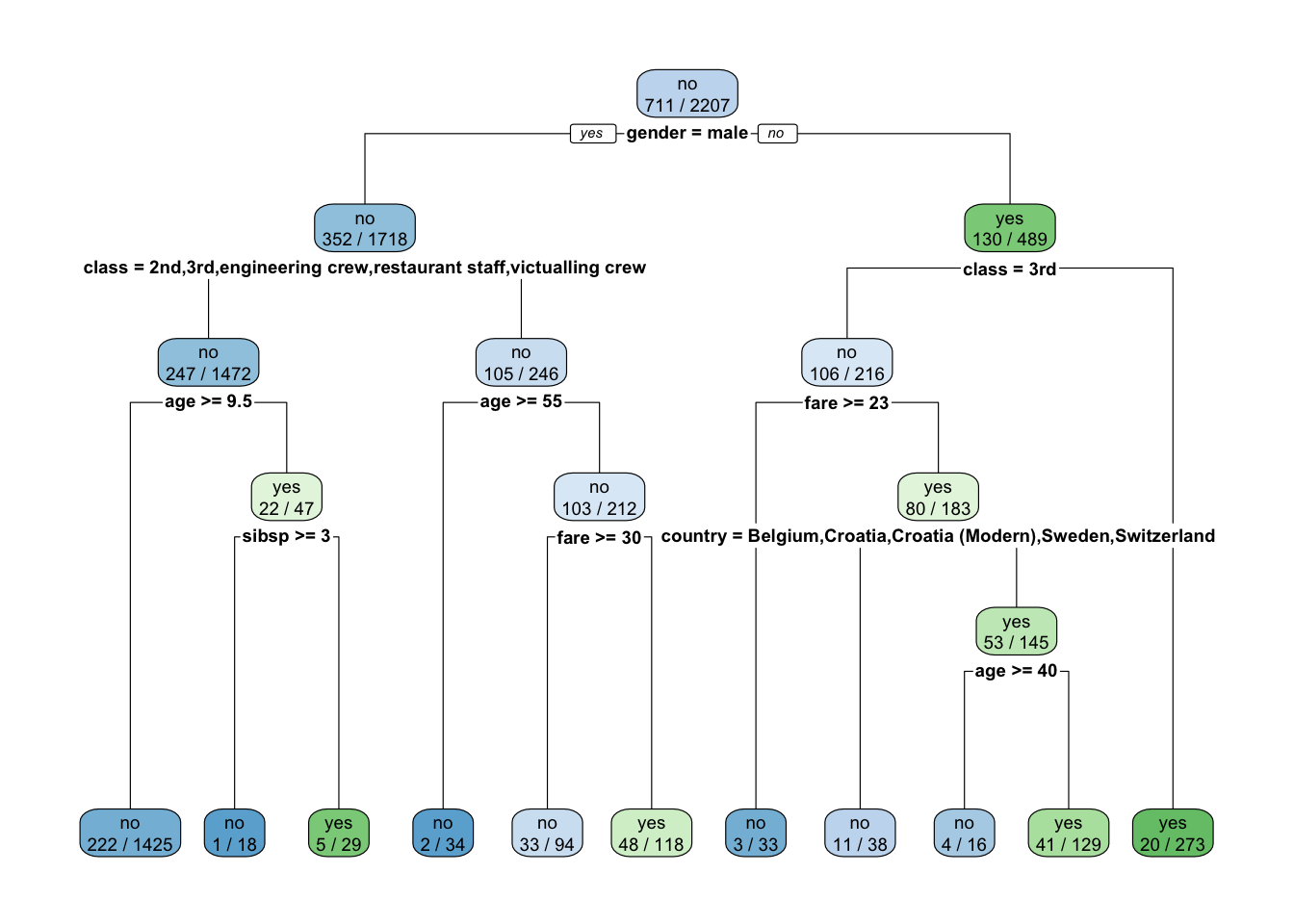
It shows gender is most important predictor for survival.

  • The a means the first level of the factor variable which here is female.
Show code
levels(titanic$gender)
[1] "female" "male"

Since the left side of the split is always the “Yes” answer to the criterion, if you are female then you go down the left branch of the tree.

  • Both female and male have the next split as class, but they have different criteria.
Show code
levels(titanic$class)
[1] "1st"              "2nd"              "3rd"              "deck crew"       
[5] "engineering crew" "restaurant staff" "victualling crew"

If female and 3rd class, then not expected to survive.

Show code
titanic |> 
  filter(gender == "female") |> 
  group_by(class) |> 
  count(survived)
# A tibble: 9 × 3
# Groups:   class [5]
  class            survived     n
  <fct>            <fct>    <int>
1 1st              no           5
2 1st              yes        139
3 2nd              no          12
4 2nd              yes         94
5 3rd              no         110
6 3rd              yes        106
7 restaurant staff yes          2
8 victualling crew no           3
9 victualling crew yes         18

If male and any class other than 1st or deck crew, survival depends upon your age and then the number of siblings and parents on board. Otherwise just your age.

Show code
summary(titanic)
    gender          age                       class            embarked   
 female: 489   Min.   : 0.1667   1st             :324   Belfast    : 197  
 male  :1718   1st Qu.:22.0000   2nd             :284   Cherbourg  : 271  
               Median :29.0000   3rd             :709   Queenstown : 123  
               Mean   :30.4367   deck crew       : 66   Southampton:1616  
               3rd Qu.:38.0000   engineering crew:324                     
               Max.   :74.0000   restaurant staff: 69                     
               NA's   :2         victualling crew:431                     
          country          fare             sibsp            parch       
 England      :1125   Min.   :  0.000   Min.   :0.0000   Min.   :0.0000  
 United States: 264   1st Qu.:  0.000   1st Qu.:0.0000   1st Qu.:0.0000  
 Ireland      : 137   Median :  7.151   Median :0.0000   Median :0.0000  
 Sweden       : 105   Mean   : 19.773   Mean   :0.2972   Mean   :0.2294  
 Lebanon      :  71   3rd Qu.: 20.111   3rd Qu.:0.0000   3rd Qu.:0.0000  
 (Other)      : 424   Max.   :512.061   Max.   :8.0000   Max.   :9.0000  
 NA's         :  81   NA's   :26        NA's   :10       NA's   :10      
 survived  
 no :1496  
 yes: 711

This is a model built on all the data. Let’s create a validation set to see how well we can predict.

  • To ensure we have the same lengths of data we will eliminate records with NAs since the tree() will eliminate them from the training data.
Show code
titanicZ <- na.omit(titanic2)
nrow(titanicZ) 
[1] 2179
Show code
set.seed(123)
Z <-  sample(nrow(titanicZ), nrow(titanicZ)/2)
tr <- tree(survived ~ gender + age + class + embarked + fare + sibsp + parch, 
           data = titanicZ, subset = Z)
tr
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 1089 1393.00 no ( 0.66208 0.33792 )  
   2) gender: female 256  302.30 yes ( 0.27734 0.72266 )  
     4) class: 3rd 109  150.00 no ( 0.55046 0.44954 )  
       8) fare < 23.07 89  122.50 yes ( 0.44944 0.55056 ) *
       9) fare > 23.07 20    0.00 no ( 1.00000 0.00000 ) *
     5) class: 1st,2nd,restaurant staff,victualling crew 147   78.19 yes ( 0.07483 0.92517 ) *
   3) gender: male 833  877.20 no ( 0.78031 0.21969 )  
     6) class: 2nd,3rd,engineering crew,restaurant staff,victualling crew 720  694.90 no ( 0.81250 0.18750 )  
      12) class: restaurant staff 34    0.00 no ( 1.00000 0.00000 ) *
      13) class: 2nd,3rd,engineering crew,victualling crew 686  680.40 no ( 0.80321 0.19679 ) *
     7) class: 1st,deck crew 113  154.10 no ( 0.57522 0.42478 ) *
Show code
plot(tr)
text(tr)

The tree looks a little different.

Let’s predict

Show code
Yhat = predict(tr, newdata = titanicZ[-Z,])
summary(Yhat)
       no               yes        
 Min.   :0.07483   Min.   :0.0000  
 1st Qu.:0.57522   1st Qu.:0.1968  
 Median :0.80321   Median :0.1968  
 Mean   :0.67045   Mean   :0.3295  
 3rd Qu.:0.80321   3rd Qu.:0.4248  
 Max.   :1.00000   Max.   :0.9252

Note these are numeric. This is the summary of the sample proportions at each node, the probabilities.

To get the classifications we have to change the type of prediction for predict.tree()

Show code
Yhat = predict(tr, newdata = titanicZ[-Z,], type = "class")
summary(Yhat)
 no yes 
870 220

So now we want to compare predicted responses against the actual testing responses.

Show code
table(Yhat, titanicZ$survived[-Z])
     
Yhat   no yes
  no  700 170
  yes  49 171

To get the prediction error rate we take the proportion of incorrect responses.

Show code
mean(Yhat != titanicZ$survived[-Z]) 
[1] 0.2009174
Show code
(table(Yhat, titanicZ$survived[-Z])[1, 2] +
    table(Yhat, titanicZ$survived[-Z])[2, 1]) / 
  sum(table(Yhat, titanicZ$survived[-Z]))
[1] 0.2009174

8.7 Example: Titanic Data with Package {rpart}

Warning

The tree::tree() function is easy to use but does have some limitations.

  • It does not handle missing values.
  • Character variables must be converted to factors.
  • It is limited to only 32 levels for factors.
  • It does not handle non-syntactic variable names, e.g. my var.
    • You can replace with names(my_df) <- stringr::str_replace_all(names(my_df), " ", "_")
  • It does not handle data.frames with the name df (see stackoverflow)

The {rpart} package provides an alternative to the {tree} package.

See the Vingette for examples.

  • The {rpart} package is based on the same fundamental algorithms as {tree} but does not have the limitations in tree::tree().
  • It also has some alternative plots provided by the {rpart.plot} package.
Note

Tree algorithms can run for a long time if you have multiple variables with many levels (more than 10) as every possible level must be checked at each split.

Show code
library(rpart)
library(rpart.plot)
trp <- rpart(survived ~ ., data = titanic)
plot(trp)
text(trp)

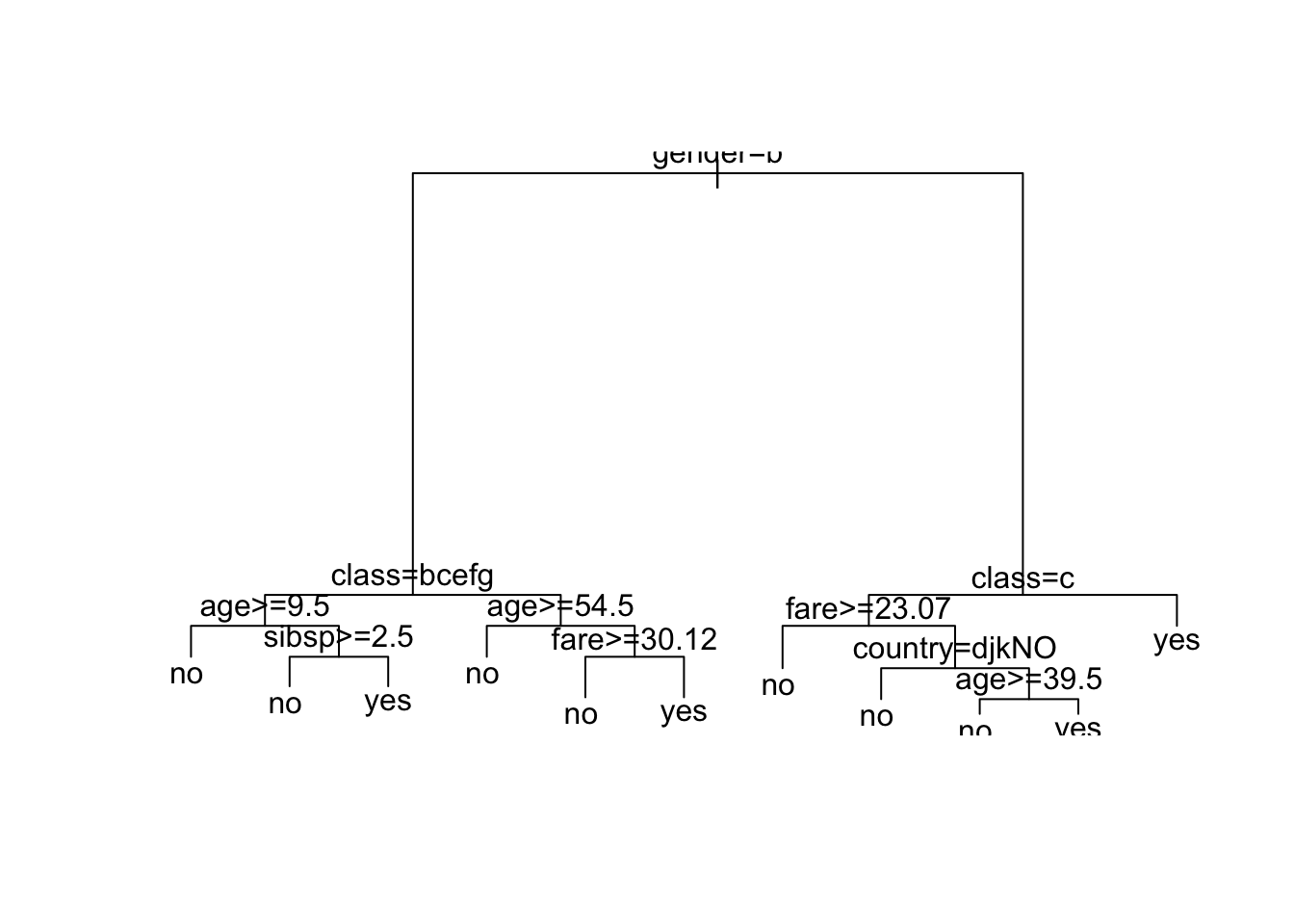
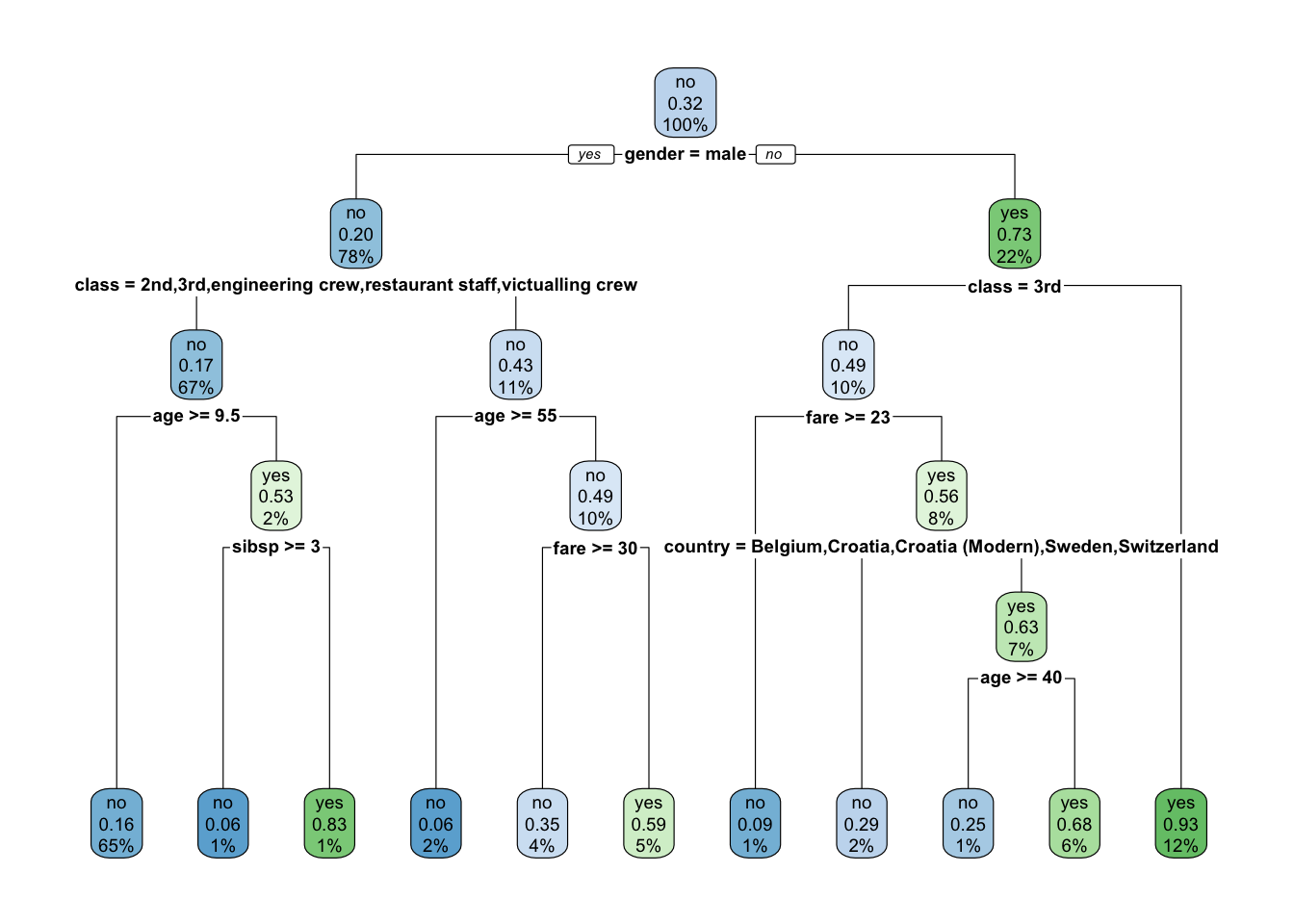
Now the top split is on male and country is in the tree.

It might be easier to see with the different plot.

  • The Second class for the node.
  • The probability of the second class.
  • Percent of observations at that level in the node.
  • You can adjust with the extra argument.
Show code
rpart.plot(trp)

Show code
rpart.plot(trp, extra = 3) #misclassification rate at the node

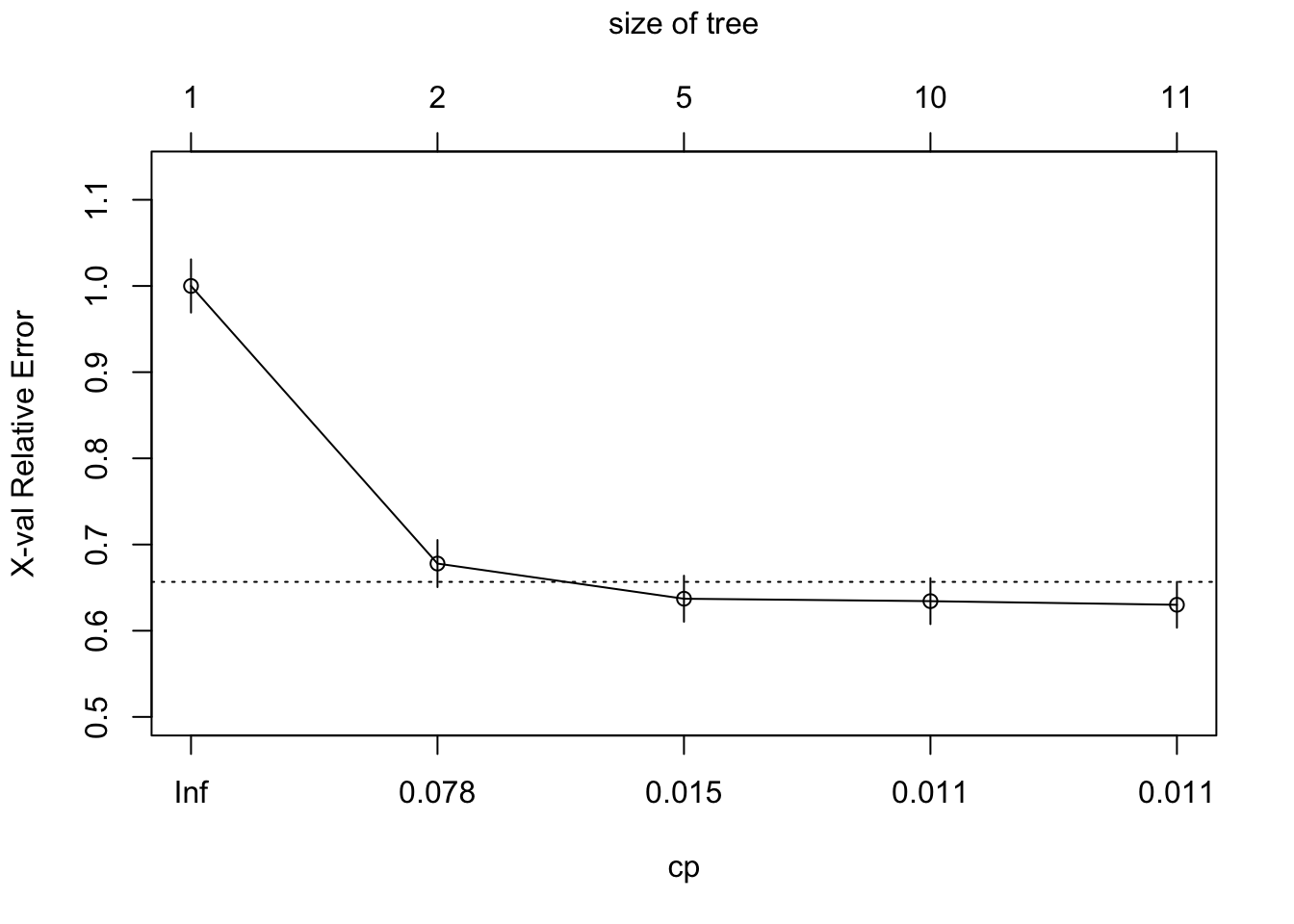
The fitting uses 10-fold cross validation by default to support later pruning.

  • You can plot the cross validation with pruning results with plotcp().
plotcp(trp)

  • The results can be found in $cptable.
    • xerror is the scaled (relative) error of the various trees. It is scaled so the largest is 1.0.
    • cp is the scaled complexity parameter.
# find best value of cp
trp$cptable
          CP nsplit rel error    xerror       xstd
1 0.32208158      0 1.0000000 1.0000000 0.03087663
2 0.01898734      1 0.6779184 0.6779184 0.02729904
3 0.01153305      4 0.6174402 0.6371308 0.02668659
4 0.01125176      9 0.5597750 0.6343179 0.02664279
5 0.01000000     10 0.5485232 0.6300985 0.02657671
min_cp <-  trp$cptable[which.min(trp$cptable[,"xerror"]),"CP"]
min_cp
[1] 0.01

Now you can create the pruned tree, which in this case is what we had in the beginning as the default for cp is .01.

trpp <- prune(trp, cp = min_cp)
rpart.plot(trpp)

Let’s create the validation set and check performance.

nrow(titanic) 
[1] 2207
set.seed(123)
Z <-  sample(nrow(titanic), nrow(titanic)/2)
trpv <- rpart(survived ~ ., data = titanic, subset = Z)
rpart.plot(trpv, faclen = 2, clip.facs = TRUE)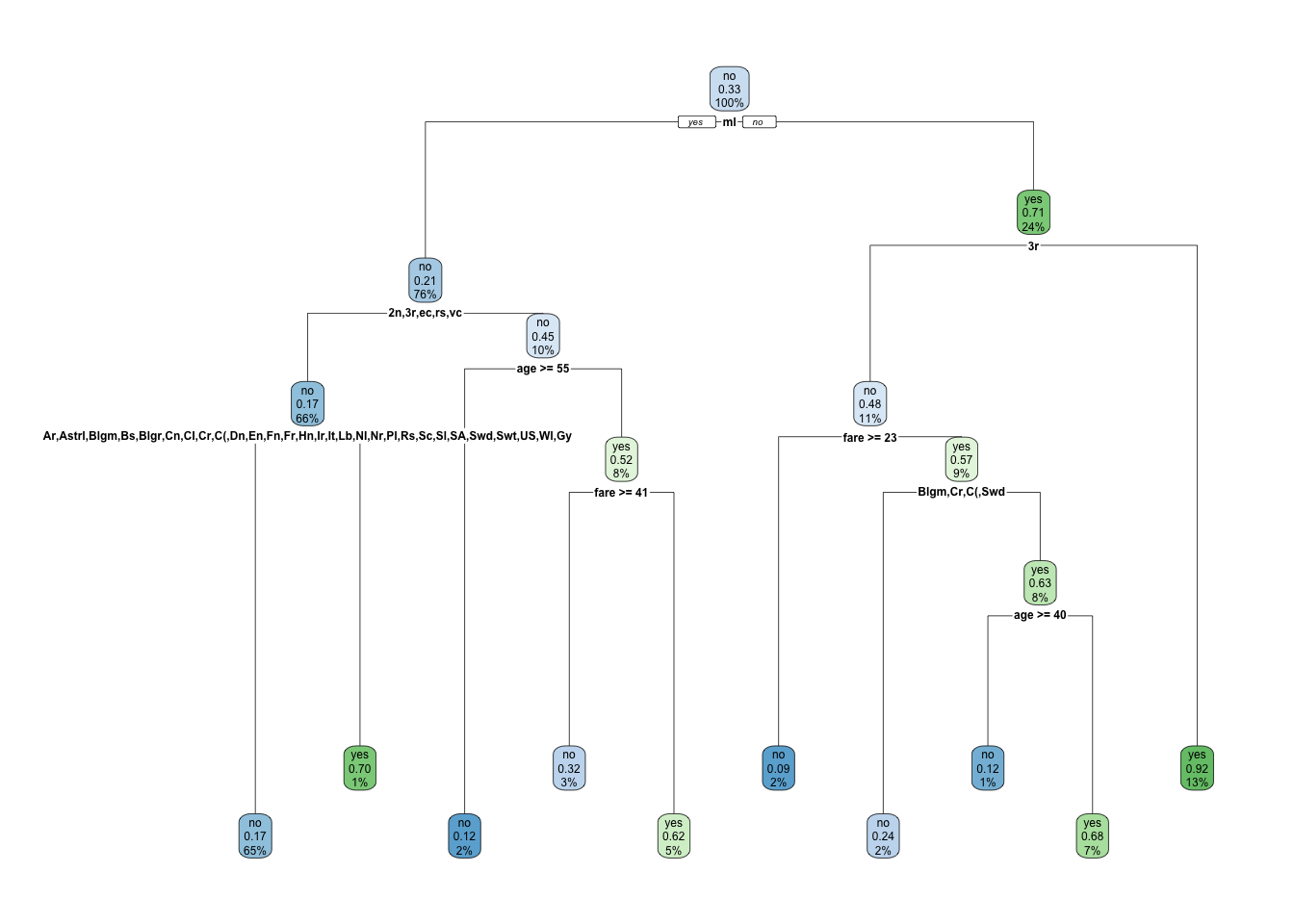

Yhat = predict(trpv, newdata = titanic[-Z,], type = "class")
summary(Yhat)
 no yes 
836 268 
table(Yhat, titanic$survived[-Z])
     
Yhat   no yes
  no  690 146
  yes  68 200
mean(Yhat != titanic$survived[-Z]) 
[1] 0.1938406
(table(Yhat, titanic$survived[-Z])[1, 2] +
    table(Yhat, titanic$survived[-Z])[2, 1]) / 
  sum(table(Yhat, titanic$survived[-Z]))
[1] 0.1938406

So using {rpart} to be able to include country resulted in a slightly better model.

Summary

Binary Decision Trees are a popular method as they are easy to interpret and explain to others.

However, they are not always the most accurate.

  • They are restrictive as they split the \(X\) space into a fixed set of splits where you have the same prediction for every observation in the region created by a split.
  • They can also have high variance as a single value can be influential on which variables are split and the split criteria values.
  • A common method for reducing variance is to average results from a number of examples, here multiple trees. This leads us to Bagging.

8.8 Bagging

Bagging (Bootstrap Aggregation) is a method for using Bootstrap to create many trees and average their predictions for each \(X_i\).

Even though we have one set of data, we can use Bootstrap methods to draw many thousands of samples and fit a tree to each sample.

That gives thousands of trees (a forest), each of which has a set of predicted values \(\hat{y}_{it}\) where

  • \(i = 1, \ldots, n\) where \(n\) is the sample size and
  • \(t = 1, \ldots, B\) where \(B\) is the number of Bootstrap trees that were generated.

With \(B\) samples, we have \(B\) trees, many which may be similar and some that will be different, so we have \(B\) predictions for each observation \(i\) in the data set.

We can then predict \(\hat{y}_i\) in regression trees by

\[ \hat{y}_i = \frac{1}{B}\sum_{t = 1}^B\hat{y}_{it} \]

In classification trees we choose the category with the highest proportion (the mode) as our prediction.

8.8.1 Example of Bagging in R

There are over 20 random forest packages in R.

We will use the package {randomForest}.

library(randomForest)

Use randomForest() to build a forest (we will use the data without rows with missing data).

data("titanic", package = "DALEX")
titanic2 <- titanic[, !(names(titanic) %in% "country")]
titanicZ <- na.omit(titanic2)

BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, 
                    data = titanicZ )
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 18.86%
Confusion matrix:
      no yes class.error
no  1367 103  0.07006803
yes  308 401  0.43441467
  • The output shows the number of trees that were built, here 500.
  • The No of variables tried at each split: is only 2 here.
    • That is because by default this function implements a random forest method which we will talk about next.
  • It also provides an OOB estimate of the error rate which we will also discuss.
  • The confusion matrix includes the class.error for each class based on OOB data: the False Negatives and the False positive Rates.

Let’s rerun but make all seven variables available for each split node by specifying mtry=7.

BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, 
                    mtry = 7, 
                    data = titanicZ)
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ, mtry = 7) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 7

        OOB estimate of  error rate: 21.11%
Confusion matrix:
      no yes class.error
no  1315 155   0.1054422
yes  305 404   0.4301834

Notice our error rate went up to 21.11% from the default approach 18.68%.

Predicting on all the data shows the training error rate looks pretty good.

Yhat <- predict(BAG, titanicZ)
table(Yhat, titanicZ$survived)
     
Yhat    no  yes
  no  1457  162
  yes   13  547
mean(Yhat != titanicZ$survived)
[1] 0.08031207

Let’s use the same validation subsets as before to get a predictive error rate while forcing it to consider all the variables for each split.

set.seed(123)
Z <-  sample(nrow(titanicZ), nrow(titanicZ)/2)

BAG <- randomForest(survived ~ gender + age + class + embarked + 
                      fare + sibsp + parch, 
                    mtry = 7, data = titanicZ[Z,] )
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ[Z, ], mtry = 7) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 7

        OOB estimate of  error rate: 24.24%
Confusion matrix:
     no yes class.error
no  630  91   0.1262136
yes 173 195   0.4701087

Let’s predict.

Yhat <- predict(BAG, newdata = titanicZ[-Z,])
table(Yhat, titanicZ$survived[-Z])
     
Yhat   no yes
  no  672 130
  yes  77 211
mean(Yhat != titanicZ$survived[-Z]) 
[1] 0.1899083

Our prediction error rate was higher at 0.189 compared to the training rate of 0.145.

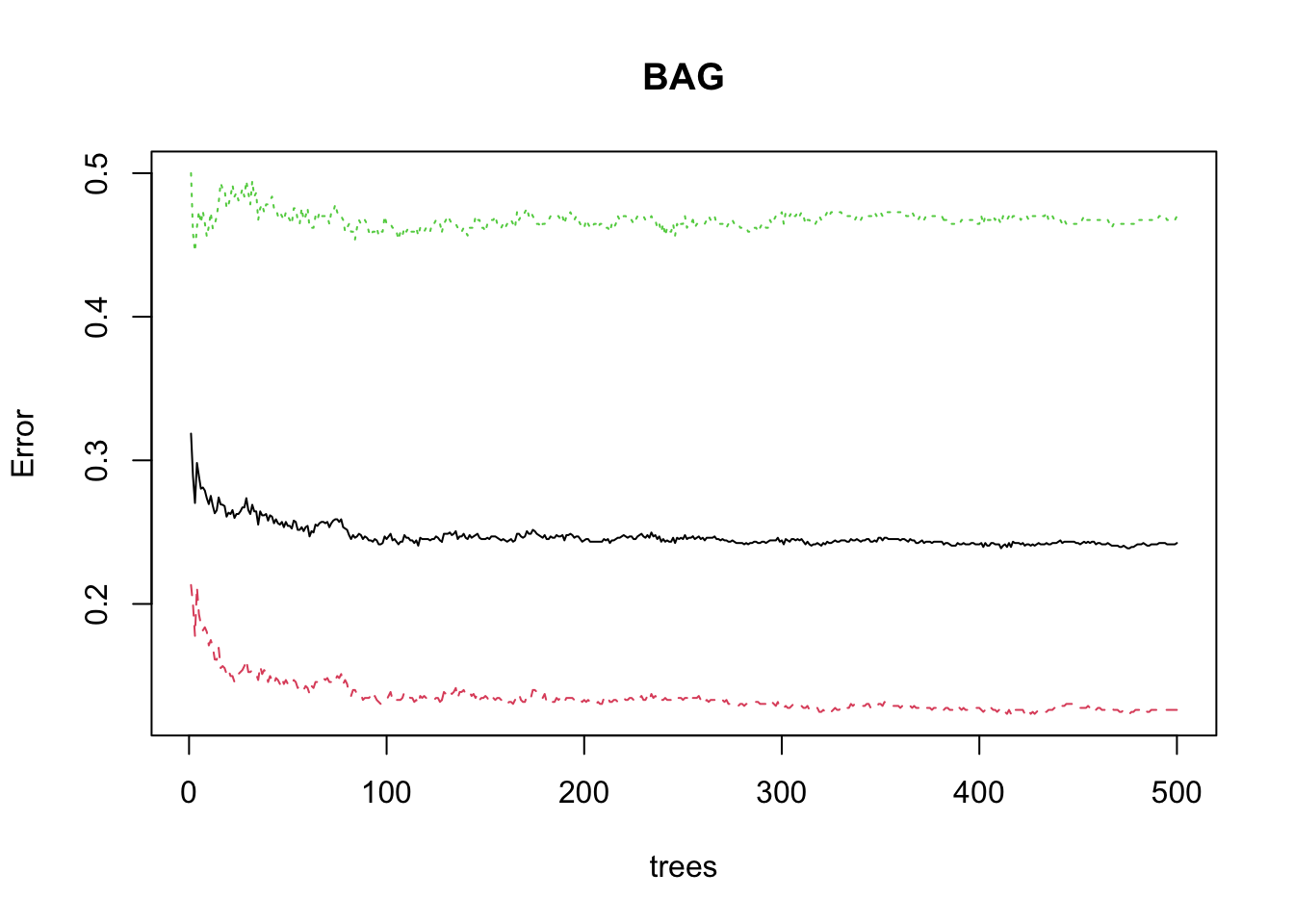
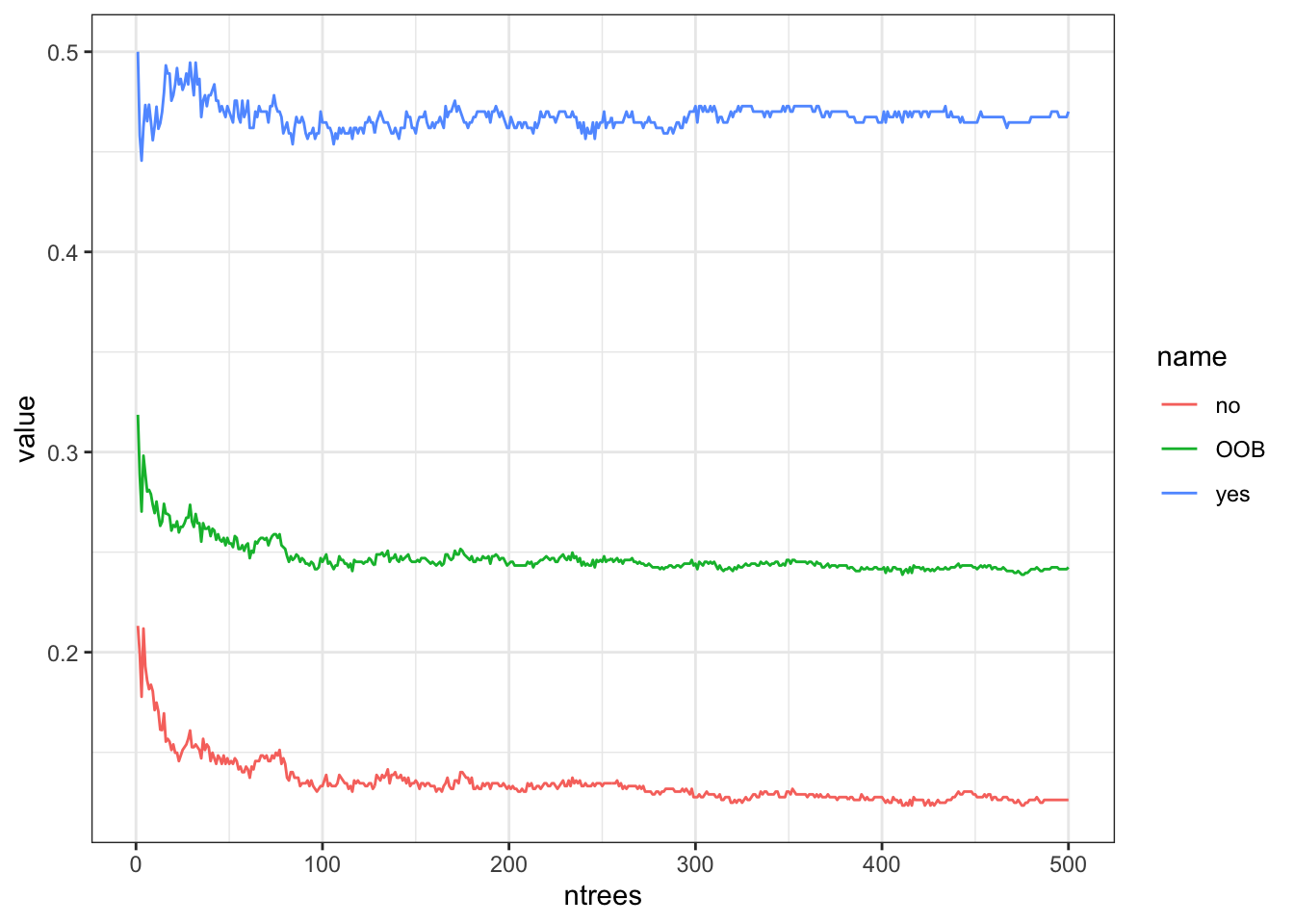
The number of trees is a tuning parameter.

We can plot the Error rate against the number of trees to see where it settles down.

plot(BAG)

plotdf <- pivot_longer(data.frame(ntrees = 1:nrow(BAG$err.rate),BAG$err.rate),
                       -ntrees)
ggplot(plotdf,aes(x = ntrees,y = value,col = name)) + 
geom_line() + theme_bw()

  • For classification trees, the BAG object includes the err.rate as a matrix of the OOB and No and Yes error rates.
  • The OOB is the average of the Yes and No error rates for each tree.
dim(BAG$err.rate)
[1] 500   3
(BAG$err.rate |> as.data.frame())$OOB |> which.min()
[1] 411

This shows the minimum OOB error was at 411 trees.

8.8.2 OOB - Out of Bag Error Rate

Recall that bootstrap is sampling with replacement so anytime observations are repeated in the sample, that means other observations are left out.

These are the Out of Bag observations.

The randomForest() output tells us how many times an observation was left out of the bag across the total number of trees.

BAG$oob.times[1:30]
 [1] 188 179 179 189 197 190 168 193 199 199 189 183 182 180 195 171 178 187 165
[20] 179 183 185 189 184 167 191 194 186 170 184

These OOB observations were used to compute the error rate for that sample since they were Not included in building the tree - they were out of the BAG of training data.

How many sampling units are typically OOB (not included) in a given bootstrap sample? Is it enough to create a meaningful test data set?

  • For a bootstrap sample we draw \(n\) units with replacement.
  • If observation \(i\) is excluded (OOB), then we can calculate the probability that occurred.
    • Each time a given observation is included with probability \(1/n\) so the complement is it is excluded with probability \(1 - 1/n\).
  • The probability \(i\) is excluded from an entire bootstrap sample with \(n\) independent random draws is thus

\[(1-1/n)^n. \tag{8.1}\]

What happens to Equation 8.1 as \(n \rightarrow \infty\)?

  • Euler’s famous identity \(e^{i\pi} + 1=0\) can be written as \((1 + x/n)^n \rightarrow e^x\text { as } n\rightarrow \infty\).
  • So, let’s use this to rewrite our formula with \(x = -1\) as :

\[(1-1/n)^n = \left(1 + \frac{-1}{\,\,n}\right)^n\rightarrow e^{-1} = \frac{1}{e} \approx 0.368 \quad\text{ as } n\rightarrow \infty\]

For \(n\) observations, this means the OOB set consists of \(\approx \frac{n}{e}\) observations for each bootstrap sample.

nrow(titanicZ[Z,])/exp(1) # expected number of OOB for a given sampled tree
[1] 400.6207
BAG$oob.times[1:30]/BAG$ntree # OOB for a given observation across the trees
 [1] 0.376 0.358 0.358 0.378 0.394 0.380 0.336 0.386 0.398 0.398 0.378 0.366
[13] 0.364 0.360 0.390 0.342 0.356 0.374 0.330 0.358 0.366 0.370 0.378 0.368
[25] 0.334 0.382 0.388 0.372 0.340 0.368
mean(BAG$oob.times/BAG$ntree) # average OOB rate for each observation 
[1] 0.3678439
Important

Thus, we have a reasonably large OOB sample that is independent of the data used to build the tree that we can use as test data.

  • Every bootstrap tree has an OOB set and the final rate is the error rate of the OOB predictions across the trees.
  • The OOB error is not calculated by comparing the prediction obtained from one tree onto its OOB samples.
  • It is calculated by using the average (or for classification, the mode) of the predictions across trees from which the sample is not used.
    • If an observation \(i\) is OOB for \(m\) trees, the OOB estimate for \(\hat{y}_i\) for a regression tree is

\[\hat{y}_{i_{OOB}} = \frac{1}{m}\sum_{i \in \text{OOB}}\hat{y}_i \quad \text{ for the set OOB of size }m \tag{8.2}\]

8.9 Random Forests

When we use the same variables to build every tree, the trees may be strongly correlated as a few variables may dominate at each split.

  • That can lead to variance inflation as we have seen before with multicollinearity where averaging across the BAG estimates does not remove as much variance as would be expected were the trees independent.

Random Forests is an approach to reduce the correlation among the trees (de-correlate them).

The approach is straightforward.

Instead of considering every variable as a candidate for each potential split, only consider a subset of \(m\) variables where \(m < p\) and select those \(m\) variables at random for each split.

  • The number of variables to be considered at a split is set by the tuning parameter \(m\).
  • The candidate variables for a split are chosen by random selection at each split.
  • This tends to exclude some variables that may be important in some trees for some splits from being in the same splits in other trees which decreases the correlations among the trees.

\(m\) is another tuning parameter you can choose.

  • A Rule of Thumb is \(m = \sqrt{p}\) for classification and \(m = p/3\) for regression.

Without setting mtry=, the default for titanic was to choose \(2 \approx \sqrt{7}\).

Let’s rerun the random forest with the default.

set.seed(123)
BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, data = titanicZ[Z,])
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ[Z, ]) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 21.49%
Confusion matrix:
     no yes class.error
no  667  54  0.07489598
yes 180 188  0.48913043
Yhat <- predict(BAG, newdata = titanicZ[-Z,])
table(Yhat, titanicZ$survived[-Z])
     
Yhat   no yes
  no  694 145
  yes  55 196
mean(Yhat != titanicZ$survived[-Z]) 
[1] 0.1834862

This produced a lower training OOB error rate and a lower predicted error rate of 0.1834 than the 0.1899 we saw with bagging.

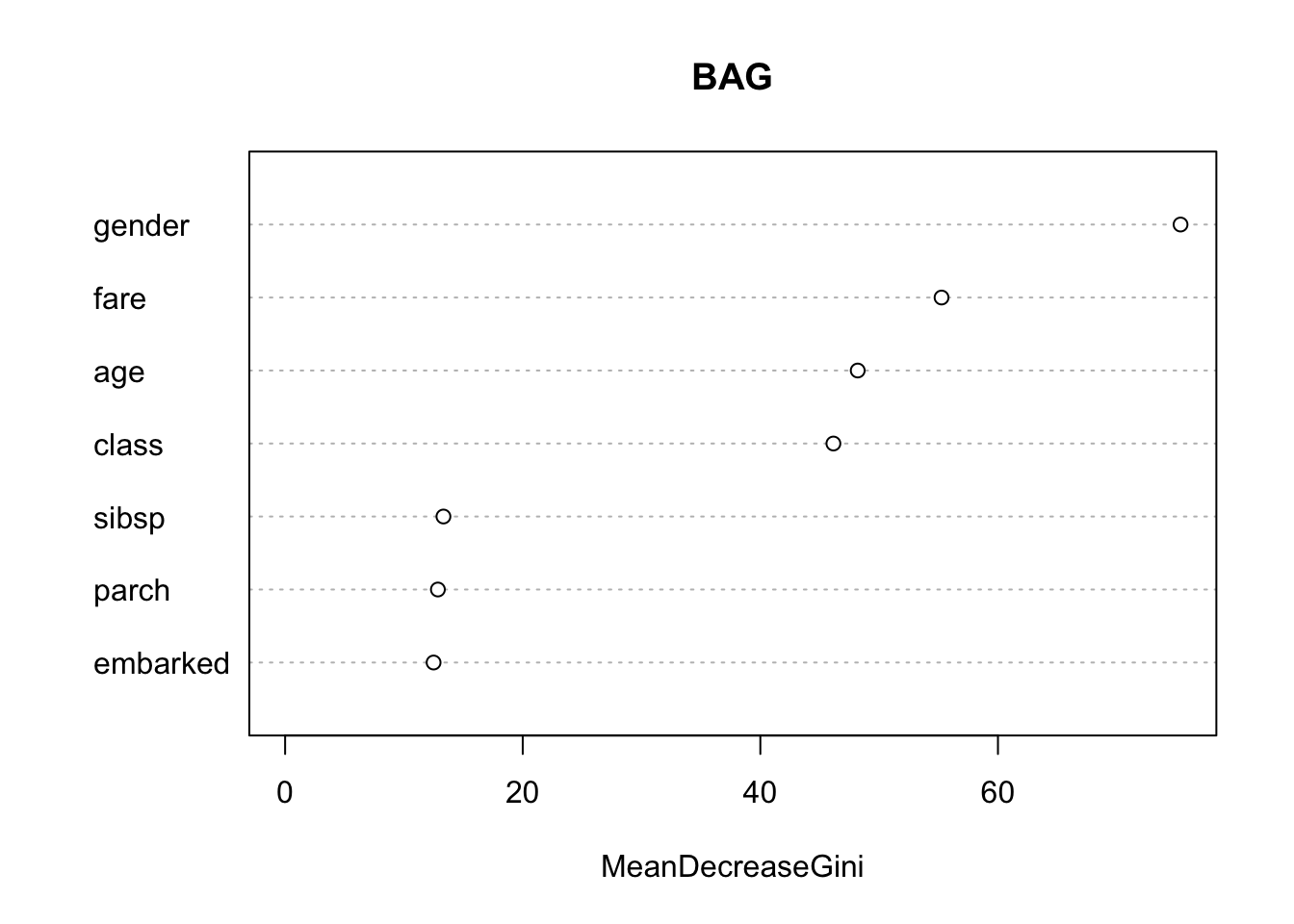
8.9.1 Importance Value for the Predictors

Since we now have 500 trees, many of which are different, how do we interpret the how important individual predictors are to the tree?

We can use the Importance value.

  • This is an average of the decrease in Gini Index (classification) or MSE (regression) for each variable across the set of \(B\) trees.
  • The larger the number, the more important the variable.

You can access the importance value directly with importance() or plot with varImpPlot().

importance(BAG)
         MeanDecreaseGini
gender           75.36817
age              48.19597
class            46.14949
embarked         12.49633
fare             55.25161
sibsp            13.32578
parch            12.85874
varImpPlot(BAG)

8.9.2 Evaluating Prediction Accuracy

Random Forest uses all the OOB data to evaluate prediction accuracy.

Each of the \(n\) observations should have an OOB estimate \(\hat{y}_{i_{OOB}}\) constructed as in Equation 8.2. These can used as the predictions to calculate an overall MSEP as follows:

\[MSEP = \frac{1}{n}\sum_i^n(\hat{y}_{i_{OOB}} - y_i)^2 \quad\text{Regression trees}\]

\[\text{Pred Error Rate } = \frac{\sum I(\hat{y}_{i_{OOB}} \neq y_i)}{n}\]

8.9.3 Tuning the Random Forest

We can tune to find the optimal number of trees and the number of variables (\(m\)) used at each split.

  • Bagging is an extreme case of Random Forest when \(m = p\).

In a random forest, the algorithm chooses the \(m\) variables at random for each split.

In R, we use arguments ntree and mtry to tune this selection.

Let’s do a quick comparison.

set.seed(123)
BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, data = titanicZ[Z,],
                    mtry = 2)
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ[Z, ], mtry = 2) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 21.49%
Confusion matrix:
     no yes class.error
no  667  54  0.07489598
yes 180 188  0.48913043
set.seed(123)
BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, data = titanicZ[Z,],
                    mtry = 3)
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ[Z, ], mtry = 3) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 3

        OOB estimate of  error rate: 22.13%
Confusion matrix:
     no yes class.error
no  655  66  0.09153953
yes 175 193  0.47554348
set.seed(123)
BAG <- randomForest(survived ~ gender + age + class + embarked +
                      fare + sibsp + parch, data = titanicZ[Z,],
                    mtry = 4)
BAG

Call:
 randomForest(formula = survived ~ gender + age + class + embarked +      fare + sibsp + parch, data = titanicZ[Z, ], mtry = 4) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 4

        OOB estimate of  error rate: 22.31%
Confusion matrix:
     no yes class.error
no  654  67  0.09292649
yes 176 192  0.47826087
  • Here it looks like 2 is better than 3 or 4 on the training data.

For quick tuning to find the optimal \(m\), use tuneRF() to find the optimal value based on OOB error rate.

  • Select a training set. Provide the X and the Y response and a starting number of parameters.
  • It will stop when it reaches the minimum or the max \(m\).
tuneRF(x = titanicZ[Z,1:7], y = titanicZ[Z,8], mtryStart = 2)
mtry = 2  OOB error = 21.67% 
Searching left ...
mtry = 1    OOB error = 22.31% 
-0.02966102 0.05 
Searching right ...
mtry = 4    OOB error = 22.87% 
-0.05508475 0.05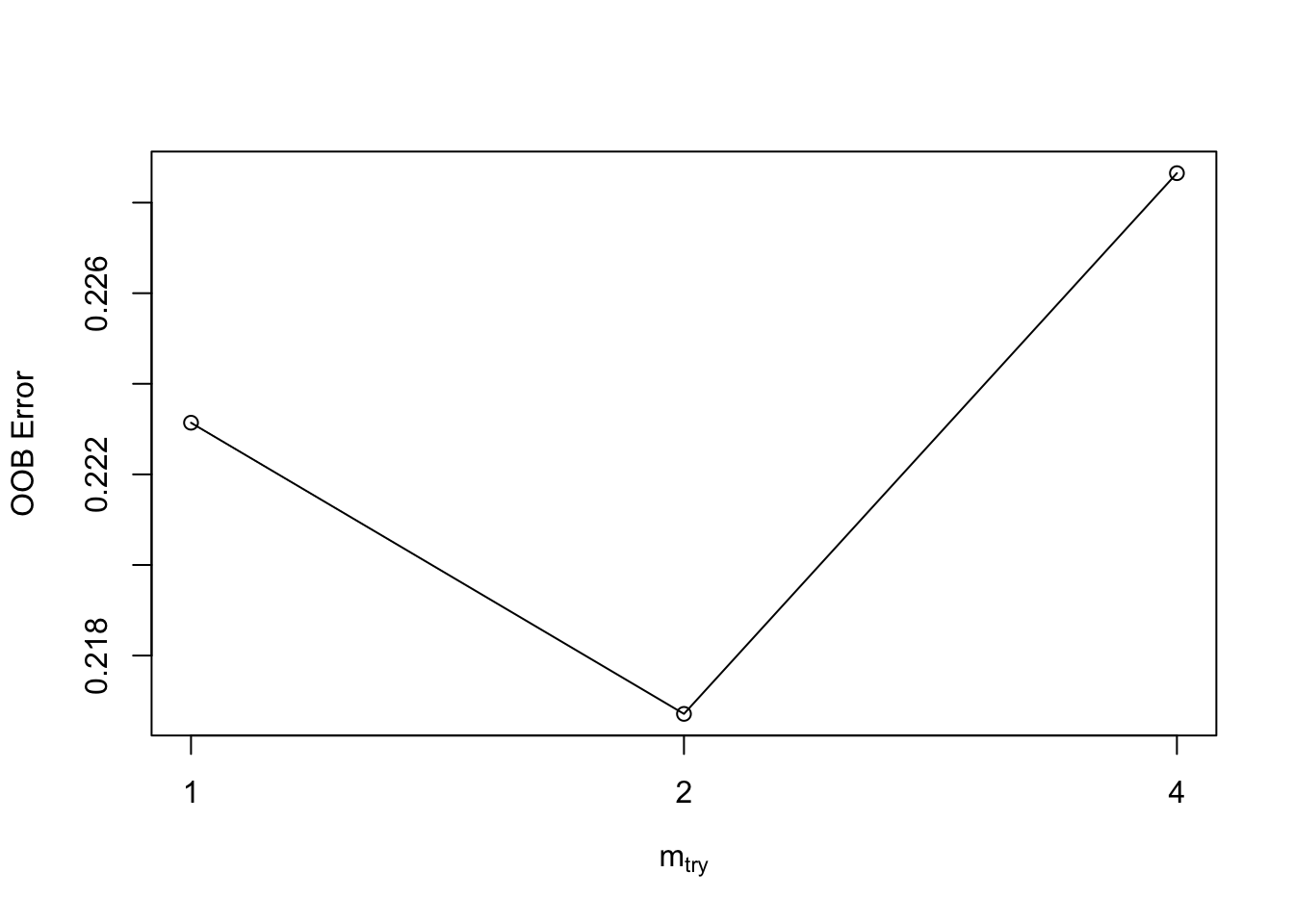 

      mtry  OOBError
1.OOB    1 0.2231405
2.OOB    2 0.2167126
4.OOB    4 0.2286501

We can tune both \(m\) and the number of trees as we will see in the next section.

8.9.4 Example of Random Forest with a Regression Tree

Let’s create a regression tree using the Housing data.

homes <- read_csv("https://raw.githubusercontent.com/rressler/data_raw_courses/main/HOME_SALES.csv")
glimpse(homes)
Rows: 522
Columns: 13
$ ID              <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ SALES_PRICE     <dbl> 360000, 340000, 250000, 205500, 275500, 248000, 229900…
$ FINISHED_AREA   <dbl> 3032, 2058, 1780, 1638, 2196, 1966, 2216, 1597, 1622, …
$ BEDROOMS        <dbl> 4, 4, 4, 4, 4, 4, 3, 2, 3, 3, 7, 3, 5, 5, 3, 5, 2, 3, …
$ BATHROOMS       <dbl> 4, 2, 3, 2, 3, 3, 2, 1, 2, 3, 5, 4, 4, 4, 3, 5, 2, 4, …
$ GARAGE_SIZE     <dbl> 2, 2, 2, 2, 2, 5, 2, 1, 2, 1, 2, 3, 3, 2, 2, 2, 2, 2, …
$ YEAR_BUILT      <dbl> 1972, 1976, 1980, 1963, 1968, 1972, 1972, 1955, 1975, …
$ STYLE           <dbl> 1, 1, 1, 1, 7, 1, 7, 1, 1, 1, 7, 1, 7, 5, 1, 6, 1, 7, …
$ LOT_SIZE        <dbl> 22221, 22912, 21345, 17342, 21786, 18902, 18639, 22112…
$ AIR_CONDITIONER <chr> "YES", "YES", "YES", "YES", "YES", "YES", "YES", "YES"…
$ POOL            <chr> "NO", "NO", "NO", "NO", "NO", "YES", "NO", "NO", "NO",…
$ QUALITY         <chr> "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MED…
$ HIGHWAY         <chr> "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", …

Let’s create a validation set.

set.seed(123)
Z <- sample(nrow(homes), nrow(homes)/2)

We will ignore ID and predict sales price using the other variables.

Let’s create a random forest using all of the variables and plot it.

set.seed(123)
 RF <- randomForest(SALES_PRICE ~ . - ID, data = homes[Z,], mtry = 11)
 RF

Call:
 randomForest(formula = SALES_PRICE ~ . - ID, data = homes[Z,      ], mtry = 11) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 11

          Mean of squared residuals: 3368183142
                    % Var explained: 81.71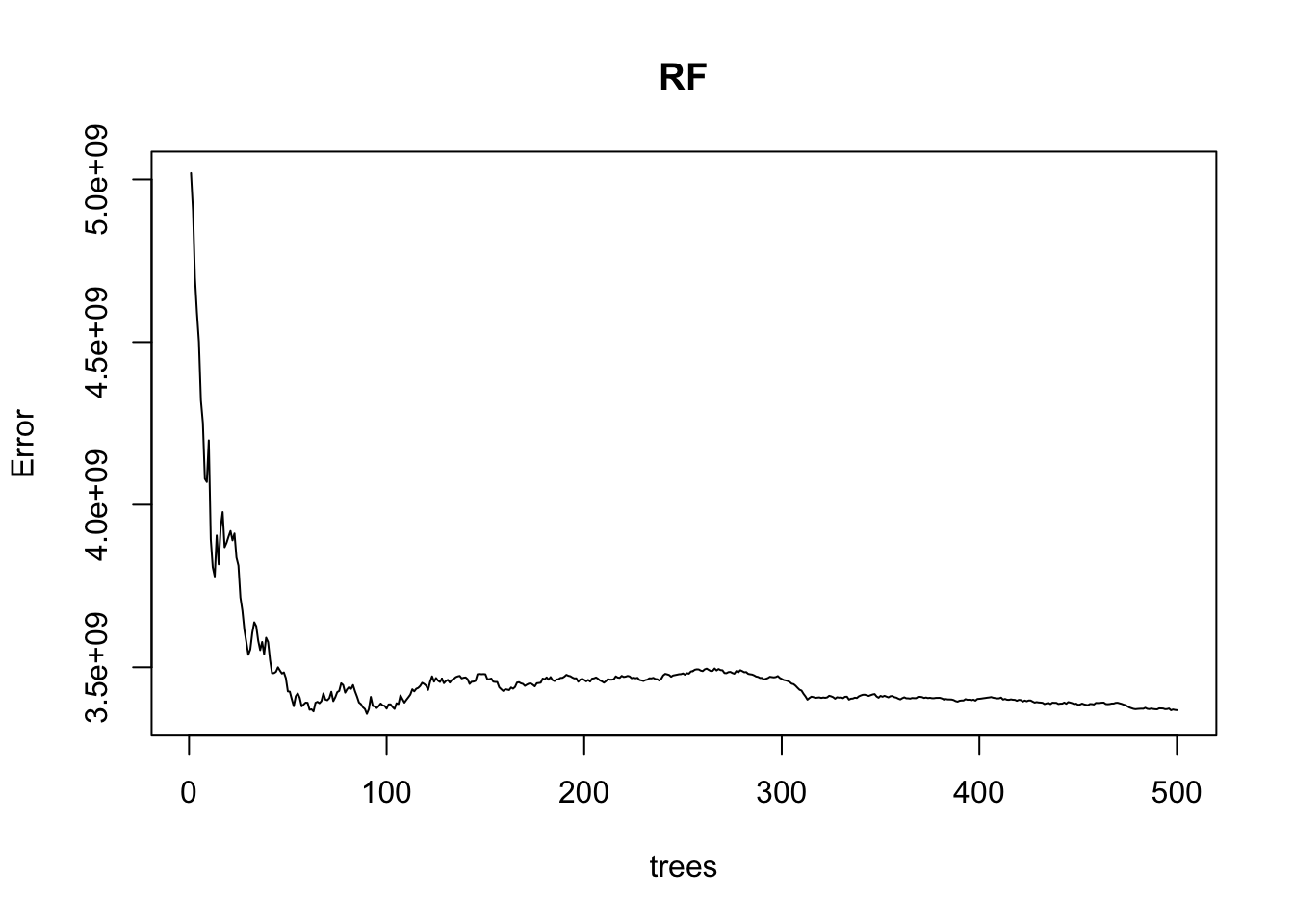
plot(RF)

We can find the number of trees that provided the minimum MSE - this is helpful to avoid excessive computations.

which.min(RF$mse)
[1] 90
 RF <- randomForest(SALES_PRICE ~ . -ID, data = homes[Z,], mtry = 11,
                    ntree = which.min(RF$mse))
 RF

Call:
 randomForest(formula = SALES_PRICE ~ . - ID, data = homes[Z,      ], mtry = 11, ntree = which.min(RF$mse)) 
               Type of random forest: regression
                     Number of trees: 90
No. of variables tried at each split: 11

          Mean of squared residuals: 3452117773
                    % Var explained: 81.25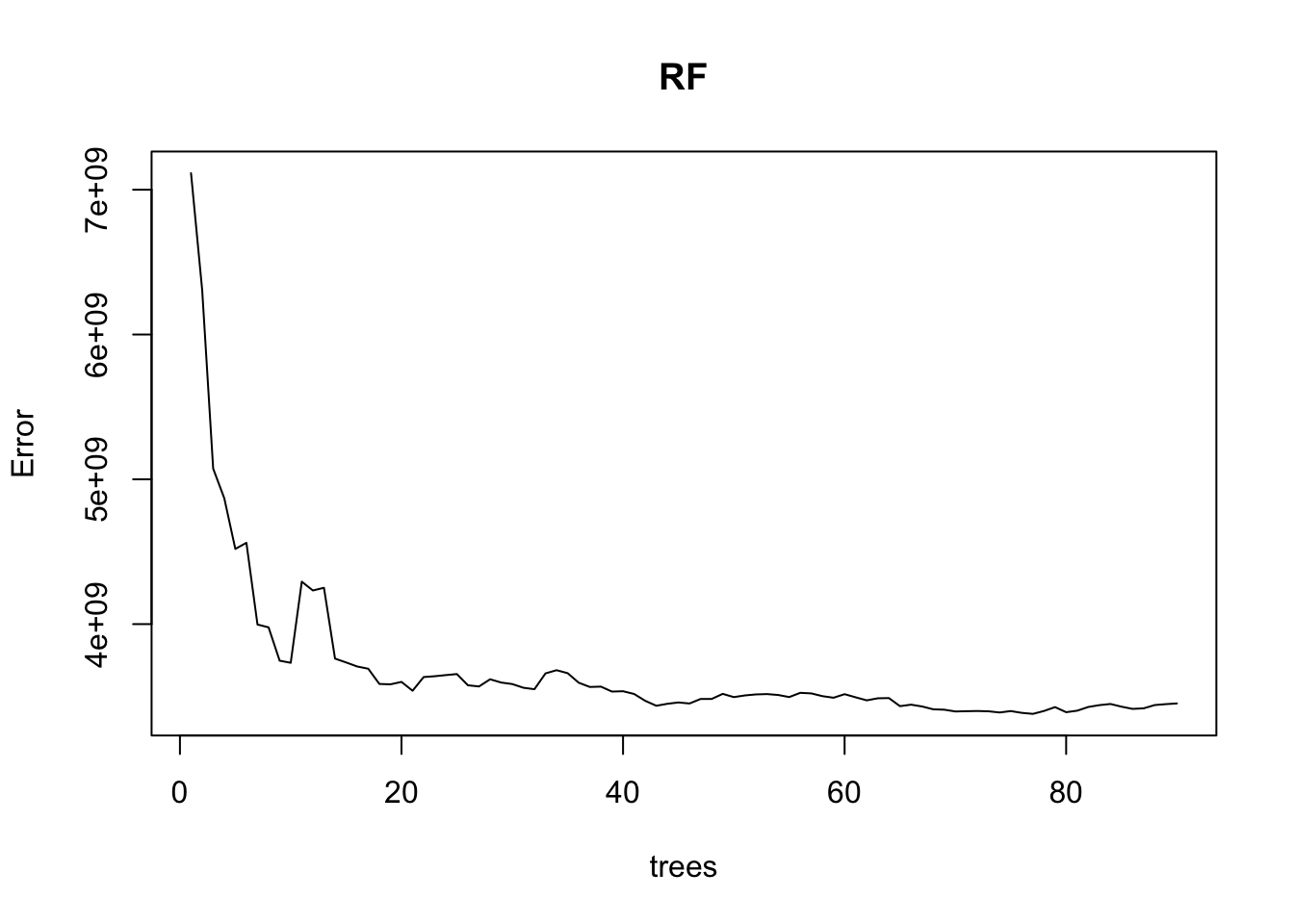
 plot(RF)

Note

We are using $mse as our performance metric.

Let’s use a for-loop to tune the number of variables \(m\) to select for the splits.

p <- length(homes) - 2 # subtract out the response and ID
RF <- OptimalTrees <- Yhat <- RMSEP <- vector(mode = "double", length = p)

Run the for-loop for each possible value of \(m\) from 1 to \(p\) to get the RMSE.

  • Create a random forest and find the optimal number of trees for that \(m\) using the training data.
  • Create a random forest with that optimal number of trees using the training data.
  • Predict the responses using the trained model with the test data.
  • Save the square root of the predicted mean square error.
set.seed(123)
for (k  in 1:p) {
  RF <- randomForest(SALES_PRICE ~ . -ID, data = homes[Z,], mtry = k)
  OptimalTrees[k] <- which.min(RF$mse)
  RF <- randomForest(SALES_PRICE ~ . -ID, data = homes[Z,], mtry = k,
                      ntree = OptimalTrees[k])
  Yhat <- predict(RF, newdata = homes[-Z,])
  RMSEP[k] <- sqrt(mean((Yhat - homes$SALES_PRICE[-Z])^2) )
}

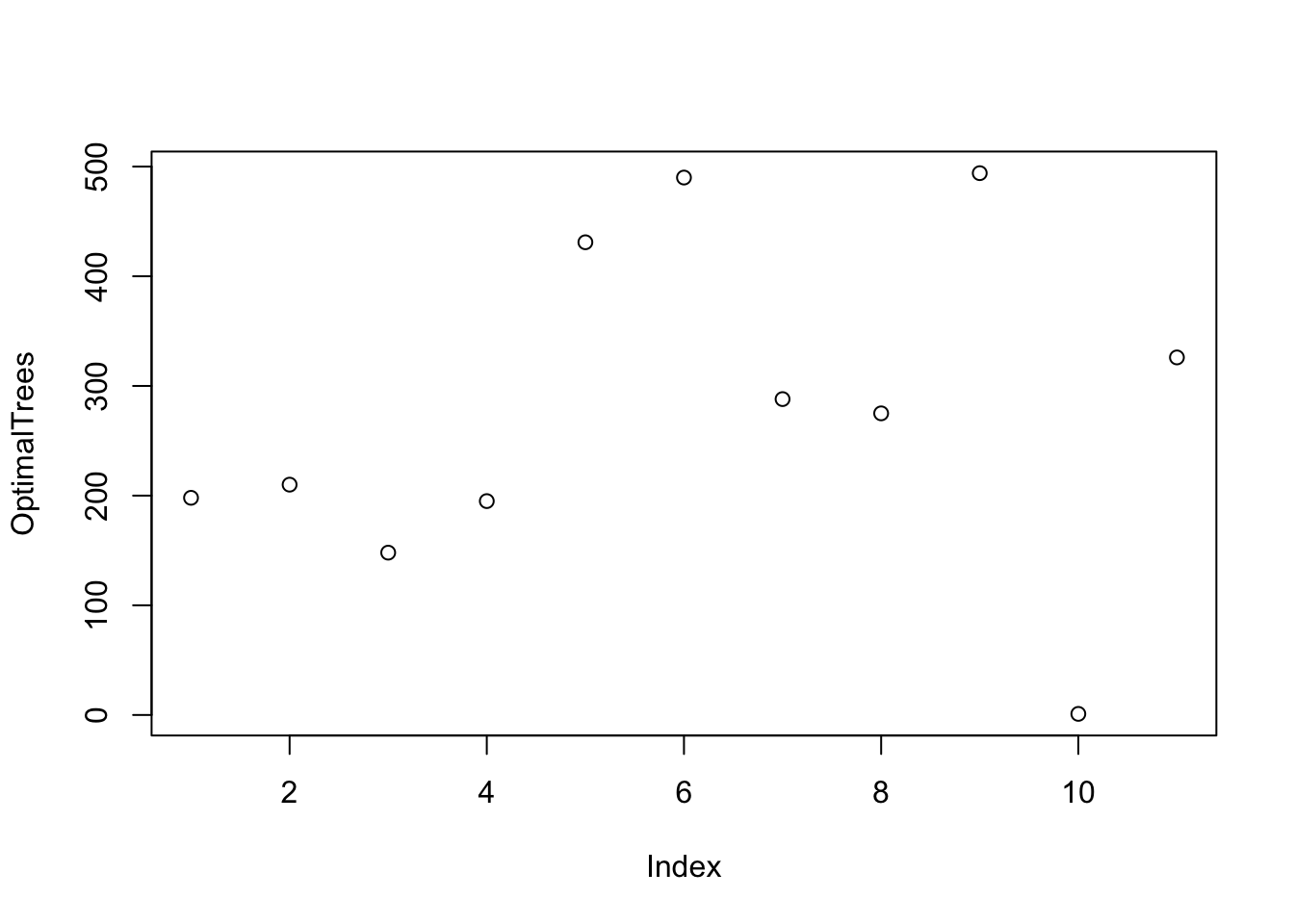
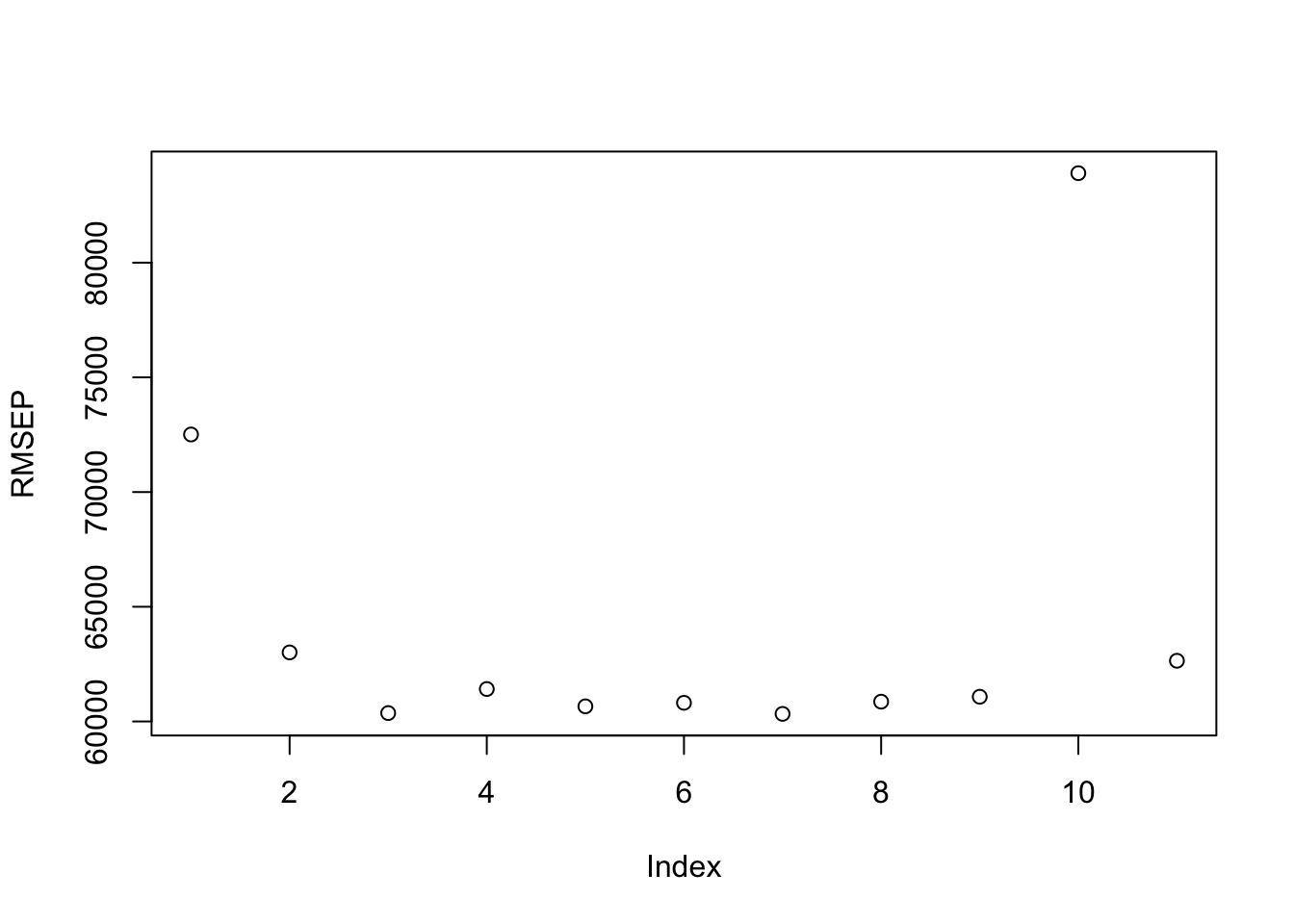
Now we can plot the optimal Trees for each \(m\) and the RMSE for each \(m\).

plot(OptimalTrees)

plot(RMSEP)

Let’s find the best combination of \(m\) and the trees for that \(m\).

which.min(RMSEP)
[1] 7
RMSEP[7]
[1] 60330.43
OptimalTrees[7]
[1] 288

So it appears that using \(m = 7\) variables for each split is optimal with 288 trees for this selection.

  • A different seed may yield different results. As an example, using 1234 yields \(m\) of 5 with 399 trees and an RMSE of 60,798.55.

8.10 Boosting

In Random Forests we build an ensemble of trees. The trees are constructed independently of each other so we could build each tree in parallel. However, even with limiting the number of variables at each split, Random Forest trees can be susceptible to extreme values.

Boosting is a general method for combining multiple weak predictors to make a stronger predictor through an additive, forward moving process.

Boosting trees is a different approach to building an ensemble of trees. The goal is to reduce the chances of overfitting and build trees in an efficient manner.

When boosting, the trees are grown sequentially so the next tree is grown using information from previously grown trees.

  • This is known as sequential learning.
  • Since each tree depends on the previous tree, they cannot be built in parallel so it can take longer to run.

Instead of building a large tree based on the original data and then pruning, boosting builds an initial (shallow) tree and then creates additional shallow trees based on the residuals from the previous fitted tree.

Let’s consider a boosted regression tree.

  • The original tree is built based on the response values \(y_i\).
  • It produces predictions \(\hat{y}_{i1}\).
  • The second tree is built using the using the residuals (\(y_i = \hat{y}_{i1)})\) as the response variable in the random forest model.
  • The two trees are combined to produce updated (improved) predictions \(\hat{y}_{i2} = \hat{y}_{i1} + \lambda \hat{y}_{i2}\).
  • In general, the \(j+1\)th tree is built using the residuals from the previous iteration \((\hat{y}_{ij-1} -\hat{y}_{ij})\) as the response variable in the \(j+1\) random forest model.
  • The algorithm stops when the chosen number of trees \(B\) has been built to create the entire ensemble.

Each new tree should be small so instead of creating one large tree, we are creating a lot of small trees, each trying to explain the remaining unexplained variance.

  • It is a stage-wise (not step-wise) process as the new tree is used with the unchanged previous trees to generate updated predictions \(\hat{y}_{ij}\).
  • This ensemble of week trees can produce strong results when generated and combined in this way.

Boosting also works on classification trees but the approach is slightly different.

Boosting can also incorporate the random forest selection of variables to be considered for each new tree.

Boosting can work for multiple distributions to describe the loss function being optimized. These include Gaussian (regression, MSE) and Bernoulli (Classification, Error rate).

Note

Consider Boosting as a method of descending the gradient of the tree in small steps by weighting the residuals from the previous step so the larger residuals influence the next tree more heavily to fit them better.

8.10.1 Boosting works with three main tuning parameters

  • \(B\): the number of trees to be built for the ensemble.
    • While this can be in the hundreds or hundreds of thousands, the algorithm tends to overfit if \(B\) gets too large.
    • You can use cross validation to select \(B\).
  • \(d\): the number of splits to use in each new tree.
    • Typically \(d\) is small, 1 or 2, so the trees learn slowly to reduce overfitting.
    • This is also known as the interaction depth.
    • You get trees with \(d+1\) terminal nodes.
  • \(\lambda\): the shrinkage parameter or the learning parameter.
    • This controls how much change can occur in a tree based on the shrinking the effects of the new tree on the prediction and thus the residuals.
    • You can also think of it as the shrinking the step size taken when moving along the gradient descent.
    • Typically \(\lambda\) is small, such as .01 or .001 and the smaller the \(\lambda\) the better the performance.
    • However, very small \(\lambda\) will increase run time as they usually require more trees, larger \(B\), to get good results.

By selecting these parameters to optimize “slow learning”, an ensemble (series), of many weakly performing trees can be combined to create an effective predictor with low risk of overfitting.

8.10.2 Example of Boosting in R

We will use the {gbm} package.

library(gbm)

Let’s use the home sales data.

We need to convert each character variable to a factor to use it in the model.

glimpse(homes)
Rows: 522
Columns: 13
$ ID              <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ SALES_PRICE     <dbl> 360000, 340000, 250000, 205500, 275500, 248000, 229900…
$ FINISHED_AREA   <dbl> 3032, 2058, 1780, 1638, 2196, 1966, 2216, 1597, 1622, …
$ BEDROOMS        <dbl> 4, 4, 4, 4, 4, 4, 3, 2, 3, 3, 7, 3, 5, 5, 3, 5, 2, 3, …
$ BATHROOMS       <dbl> 4, 2, 3, 2, 3, 3, 2, 1, 2, 3, 5, 4, 4, 4, 3, 5, 2, 4, …
$ GARAGE_SIZE     <dbl> 2, 2, 2, 2, 2, 5, 2, 1, 2, 1, 2, 3, 3, 2, 2, 2, 2, 2, …
$ YEAR_BUILT      <dbl> 1972, 1976, 1980, 1963, 1968, 1972, 1972, 1955, 1975, …
$ STYLE           <dbl> 1, 1, 1, 1, 7, 1, 7, 1, 1, 1, 7, 1, 7, 5, 1, 6, 1, 7, …
$ LOT_SIZE        <dbl> 22221, 22912, 21345, 17342, 21786, 18902, 18639, 22112…
$ AIR_CONDITIONER <chr> "YES", "YES", "YES", "YES", "YES", "YES", "YES", "YES"…
$ POOL            <chr> "NO", "NO", "NO", "NO", "NO", "YES", "NO", "NO", "NO",…
$ QUALITY         <chr> "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MEDIUM", "MED…
$ HIGHWAY         <chr> "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", "NO", …
homes <- mutate(homes, across(where(is.character), as.factor))

8.10.2.1 Building the Boosted Ensemble

Now we can build the model with the training data and see the summary.

  • Set n.trees=5000to start instead of the default 100.
  • the default d is interaction.depth=1.
  • The default \(\lambda\) is shrinkage=0.1.
  • Set distribution ="gaussian" since we are doing least squares regression.
  • The output is a gbm.object. See ?gbm.object for details.
  • Then check the summary() (?summary.gbm) to see the relative influence of each variable in the ensemble model normalized to 100.
    • For distribution="gaussian" this returns exactly the reduction of squared error attributable to each variable.
    • Note: the code is in the print.gbm.R function and you cannot adjust the barplot attributes.
set.seed(123)
Z <- sample(nrow(homes), nrow(homes)/2)
set.seed(123)
boosth <- gbm(SALES_PRICE ~ . - ID, data = homes[Z,], 
              n.trees = 5000, distribution = "gaussian")
boosth
gbm(formula = SALES_PRICE ~ . - ID, distribution = "gaussian", 
    data = homes[Z, ], n.trees = 5000)
A gradient boosted model with gaussian loss function.
5000 iterations were performed.
There were 11 predictors of which 10 had non-zero influence.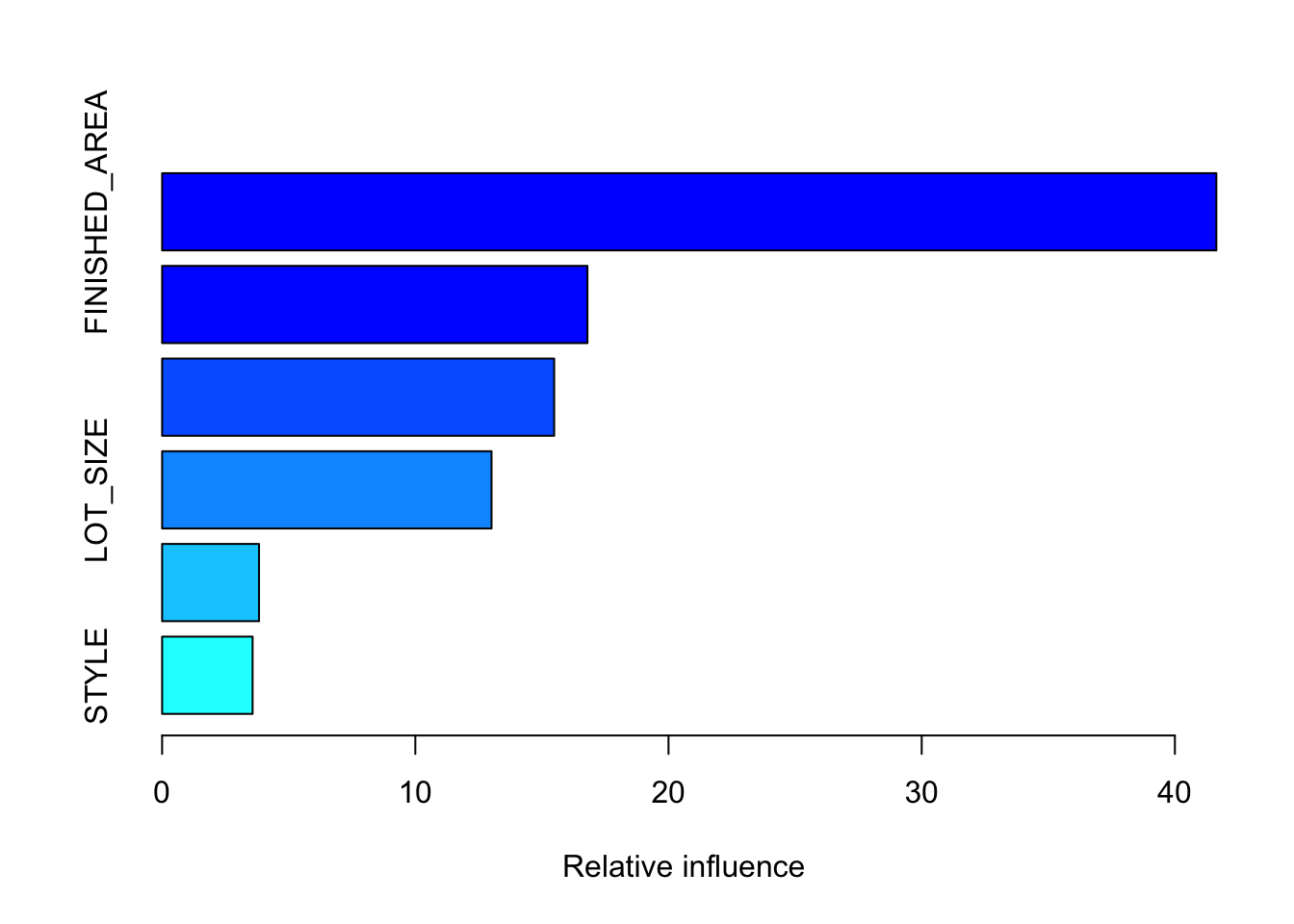
summary(boosth, cBars = 6)

                            var    rel.inf
FINISHED_AREA     FINISHED_AREA 41.6378622
YEAR_BUILT           YEAR_BUILT 16.7978453
QUALITY                 QUALITY 15.4843121
LOT_SIZE               LOT_SIZE 13.0096535
BEDROOMS               BEDROOMS  3.8274367
STYLE                     STYLE  3.5735513
BATHROOMS             BATHROOMS  3.4374819
GARAGE_SIZE         GARAGE_SIZE  1.5708073
POOL                       POOL  0.4075263
AIR_CONDITIONER AIR_CONDITIONER  0.2535233
HIGHWAY                 HIGHWAY  0.0000000

To see a given tree structure use pretty.gbm.tree(object, i.tree= j) where j is the number of the tree.

  • This is not necessary for the analysis but can help to understand what the individual “weak” trees might look like.
pretty.gbm.tree(boosth) # default of i.tree is 1
  SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
0        0     2613.5000        1         2           3   1.502409e+12    130
1       -1    -6567.2724       -1        -1          -1   0.000000e+00     92
2       -1    17069.0592       -1        -1          -1   0.000000e+00     38
3       -1      341.8091       -1        -1          -1   0.000000e+00    130
  Prediction
0   341.8091
1 -6567.2724
2 17069.0592
3   341.8091
pretty.gbm.tree(boosth, i.tree = 3000)
  SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
0        6   22013.50000        1         2           3     2637144773    130
1       -1    -588.11907       -1        -1          -1              0     57
2       -1     319.57564       -1        -1          -1              0     73
3       -1     -78.41358       -1        -1          -1              0    130
  Prediction
0  -78.41358
1 -588.11907
2  319.57564
3  -78.41358

The output is a data frame where each row is a node in the tree.

  • The left column is the node number with the root being 0.
    • Note: gbm() uses a c++ engine for the boosting which returns variable indices starting with 0 so add 1 to get the variable.
  • SplitVar: the index of which variable is split. The -1 indicates a terminal or leaf node.
  • SplitCodePred: If the split variable is continuous this is the split point. If it’s categorical is the index of object$c.split that describes the categorical split. If the node is a terminal node ,this is the prediction.
  • The prediction is weighted by the learning rate.
  • The last row is the node to use if there is an NA in the data (as indicated by the index in the MissingNode variable for the root node). That is why there are three leaf nodes for a binary tree with one split.

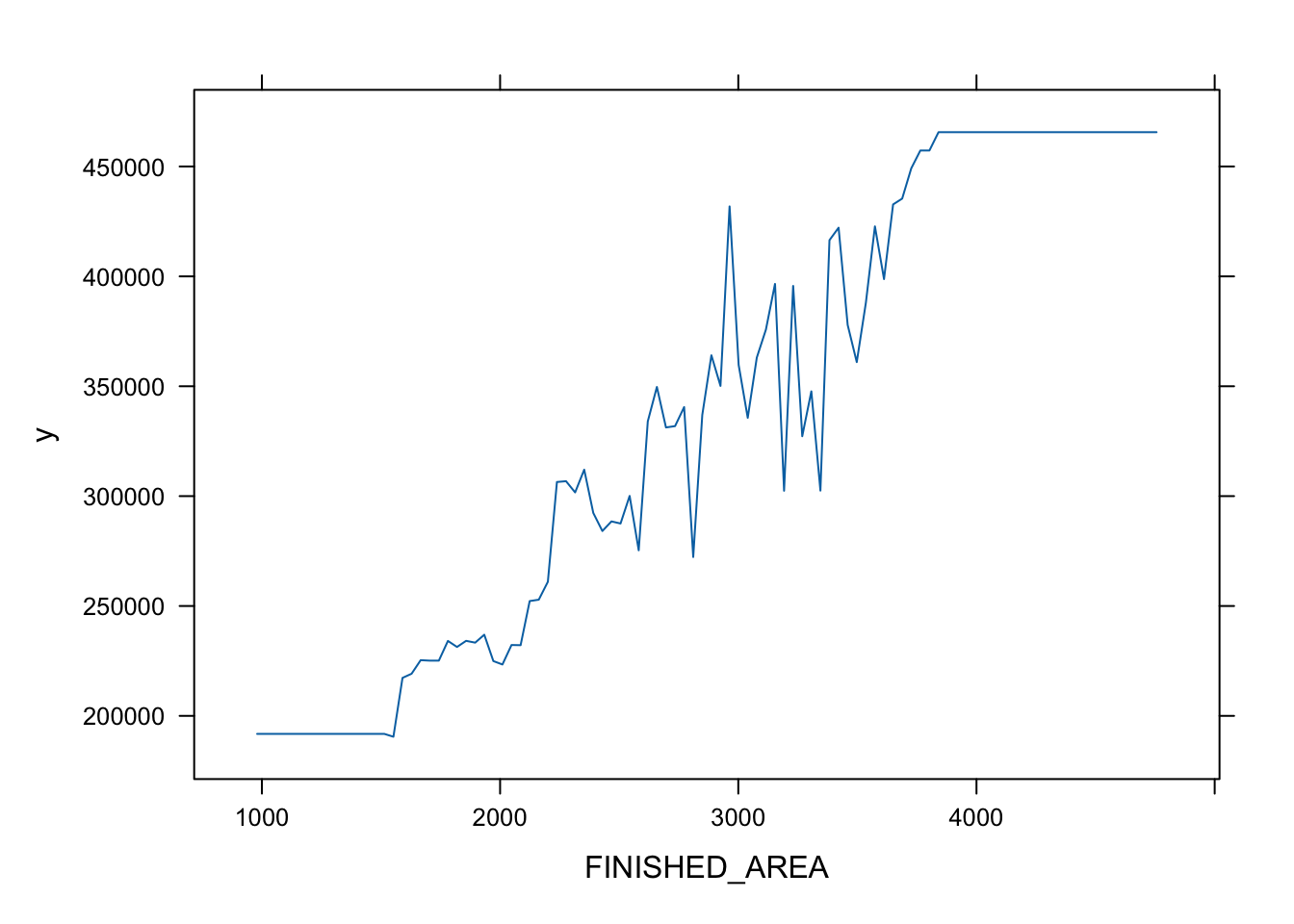
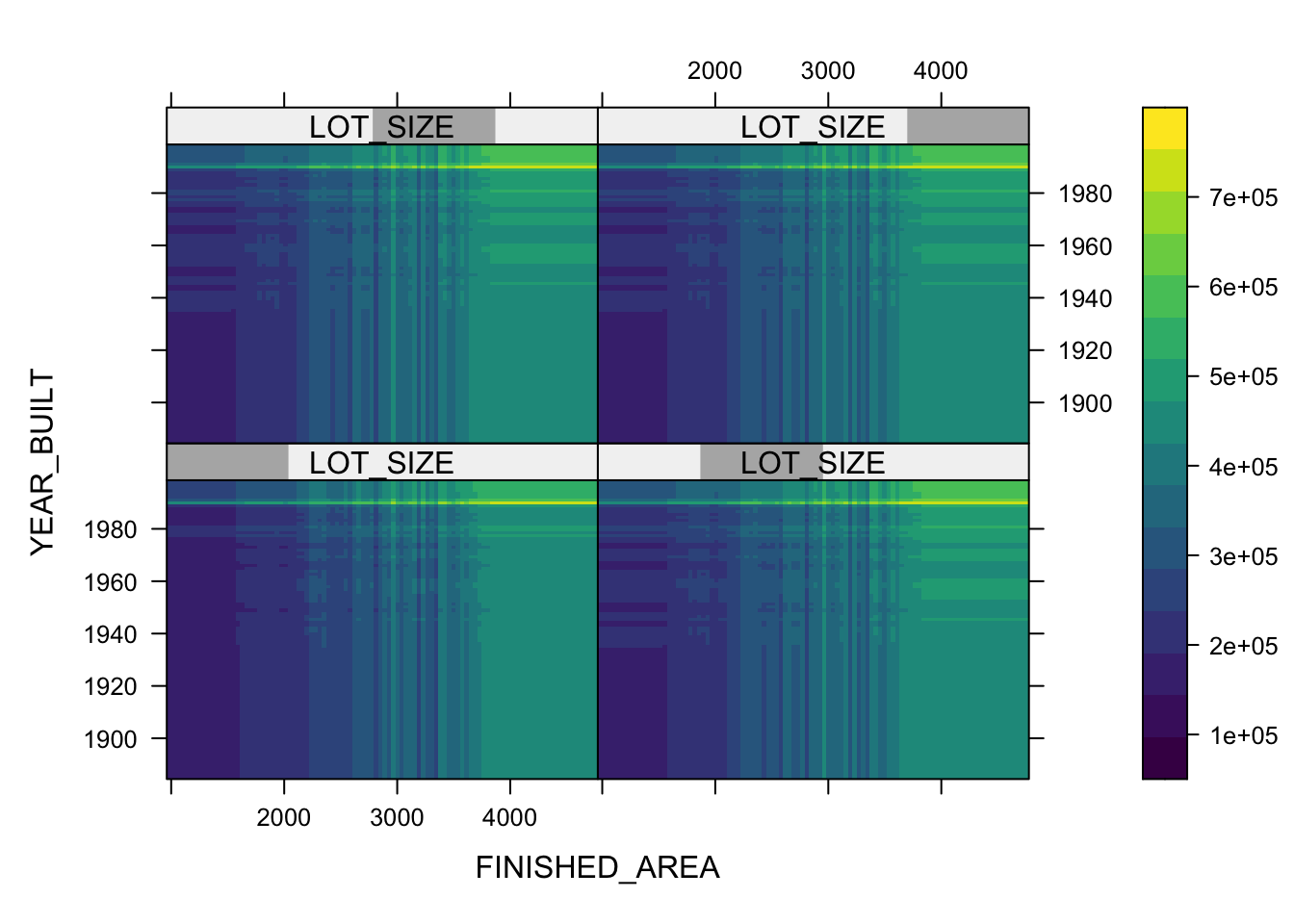
Partial variable plots show the marginal effect of individual variables on the response variable ( here \(Y\) is SALES_PRICE) after all others are accounted for. (?plot.gbm)

  • Let’s look at the top three.
plot(boosth, "FINISHED_AREA")
plot(boosth, "YEAR_BUILT")
plot(boosth, "QUALITY")

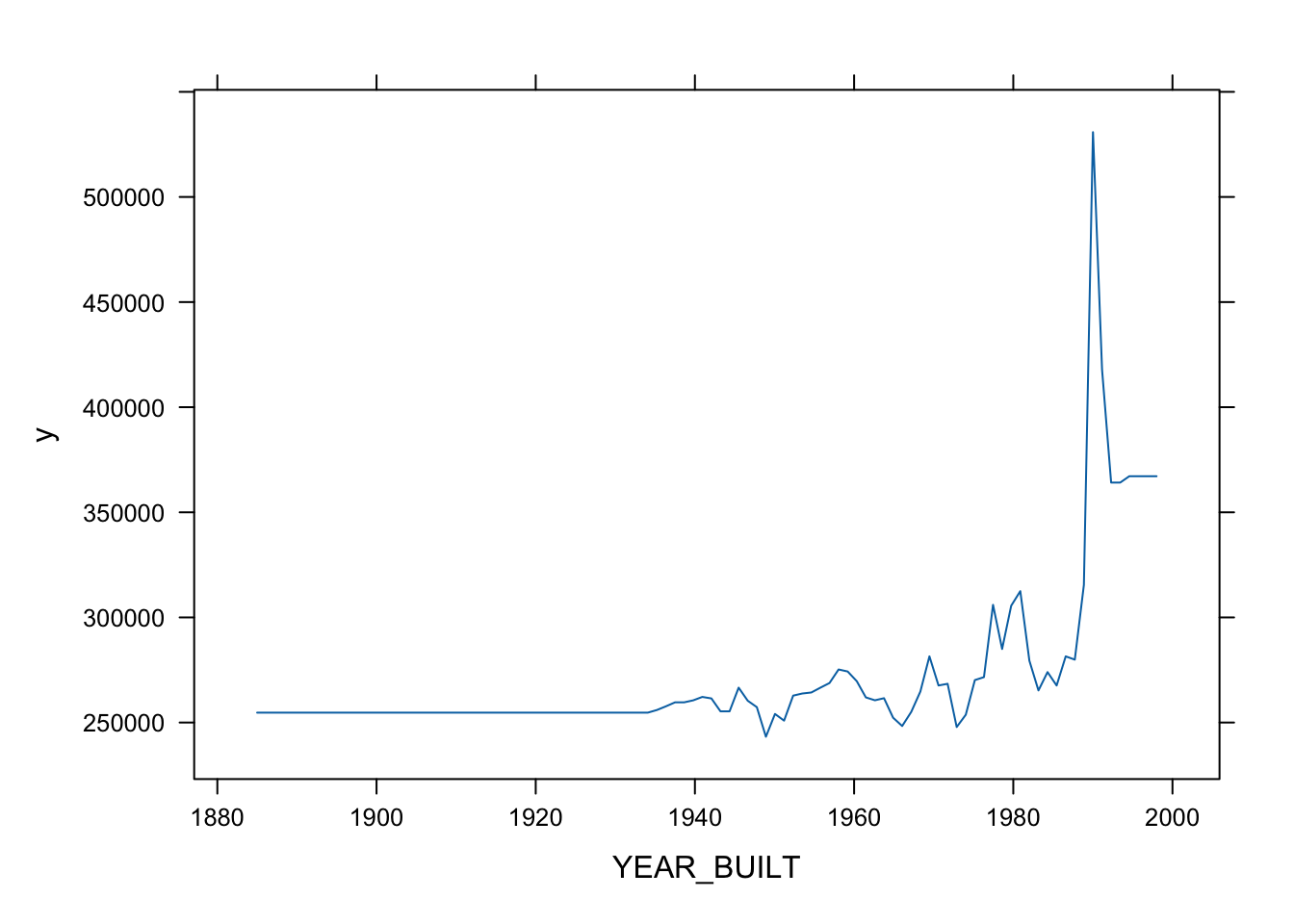
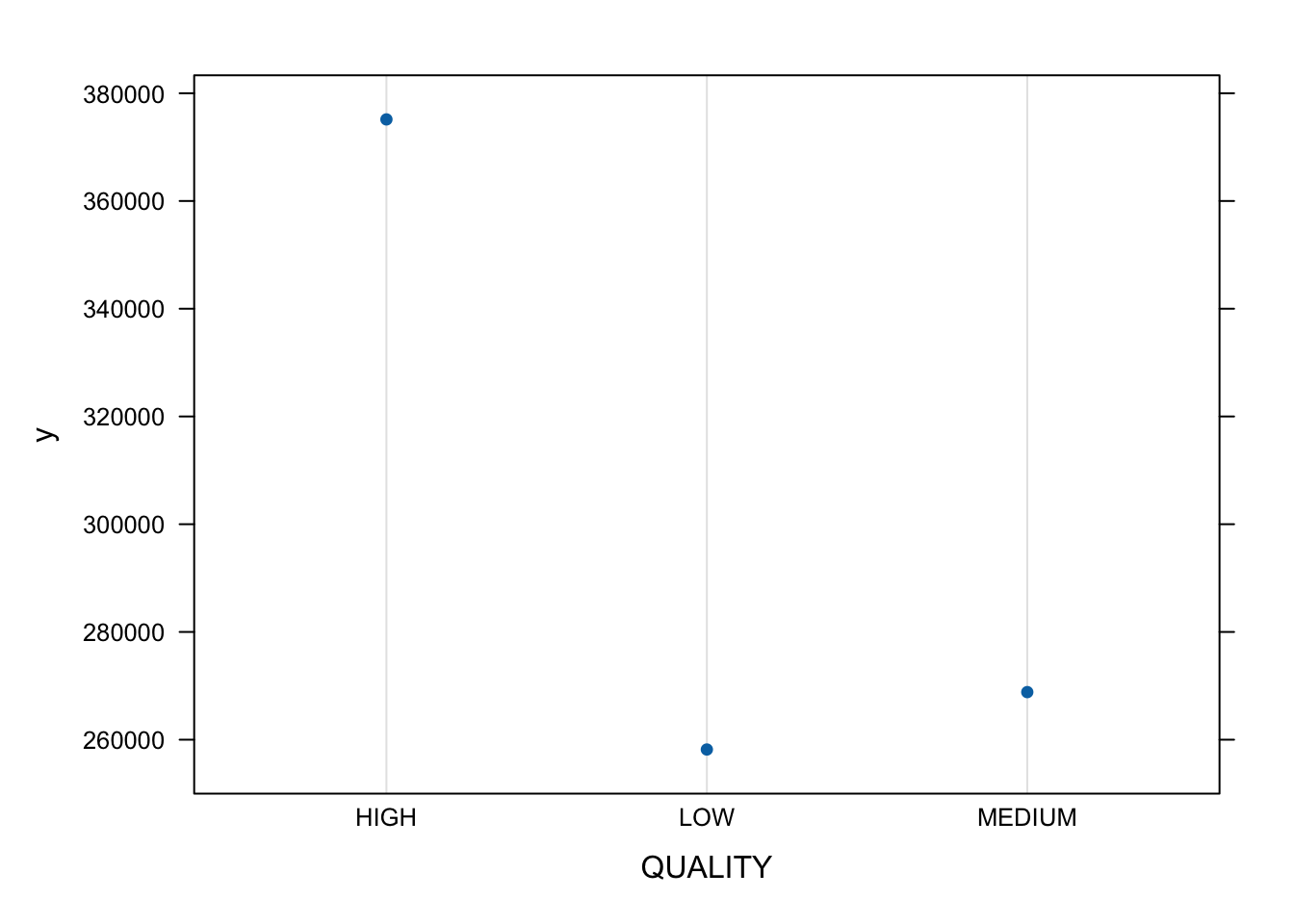
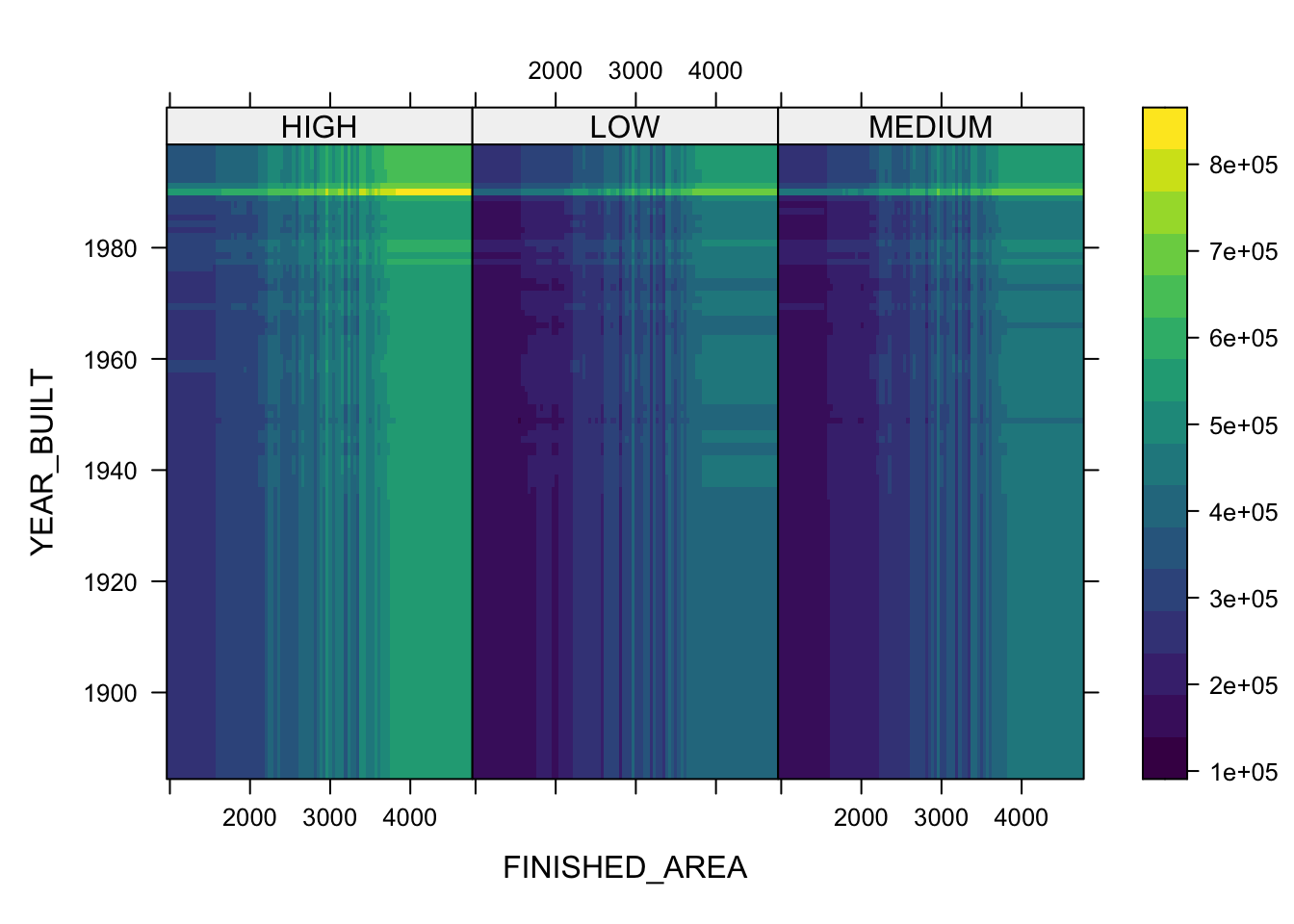
  • You can also plot two or three variables to get a contour plot.
plot(boosth, c("FINISHED_AREA", "YEAR_BUILT"))
plot(boosth, c("FINISHED_AREA", "YEAR_BUILT", "QUALITY"))
plot(boosth, c("FINISHED_AREA", "YEAR_BUILT", "LOT_SIZE"))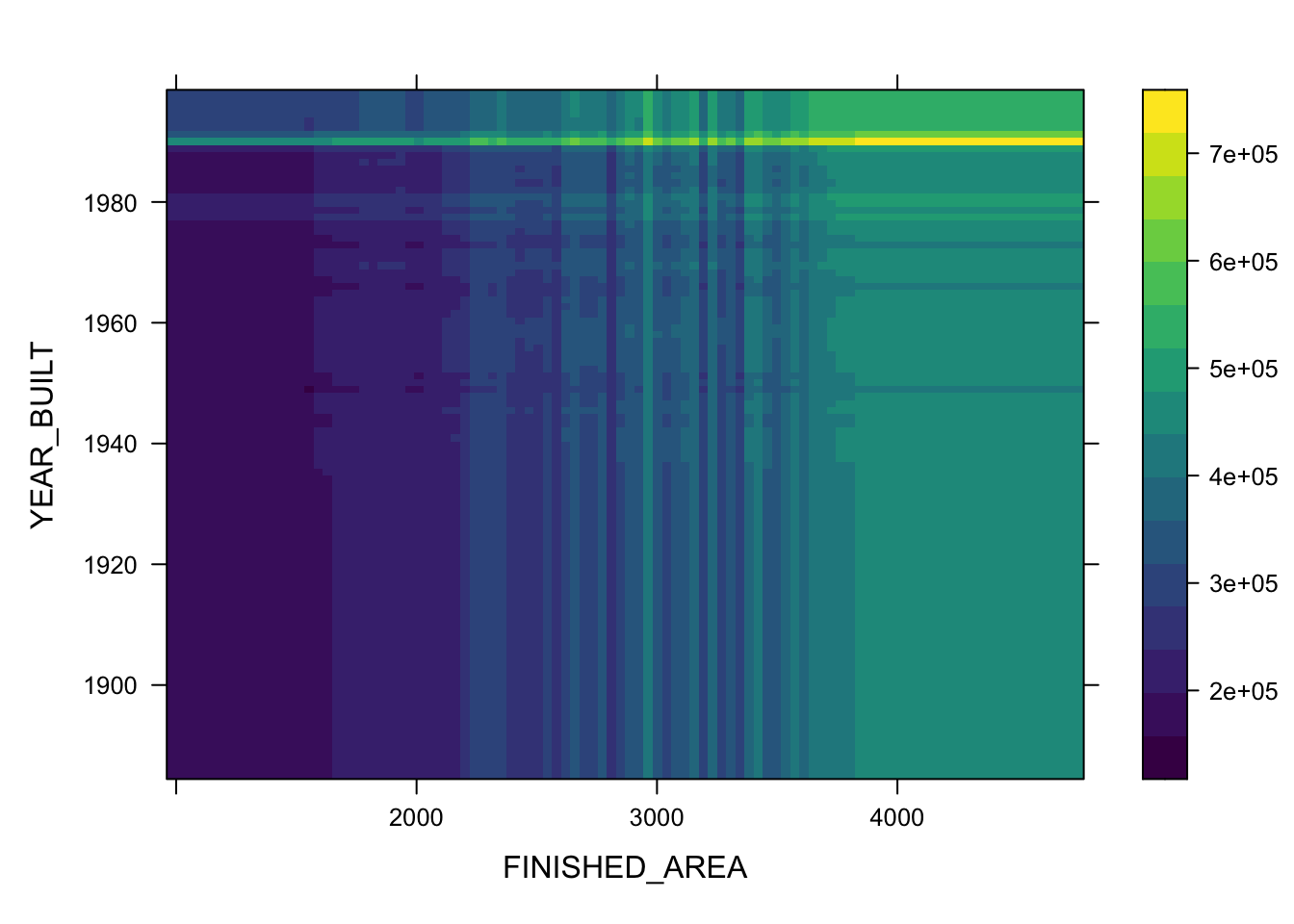

8.10.3 Prediction

Let’s predict.

  • ?predict.gbm
  • If doing for classification with distribution="bernoulli", use type="response" to get the predictions in the levels of Y, instead of the log-odds.
Yhat <- predict(boosth, newdata = homes[-Z,], n.trees = 5000)
mean((Yhat - homes$SALES_PRICE[-Z])^2)^.5
[1] 67482.13

Let’s adjust the shrinkage parameter.

set.seed(123)
boosth <- gbm(SALES_PRICE ~ . - ID, data = homes[Z,], 
              n.trees = 5000, shrinkage = .001,
              distribution = "gaussian")
summary(boosth)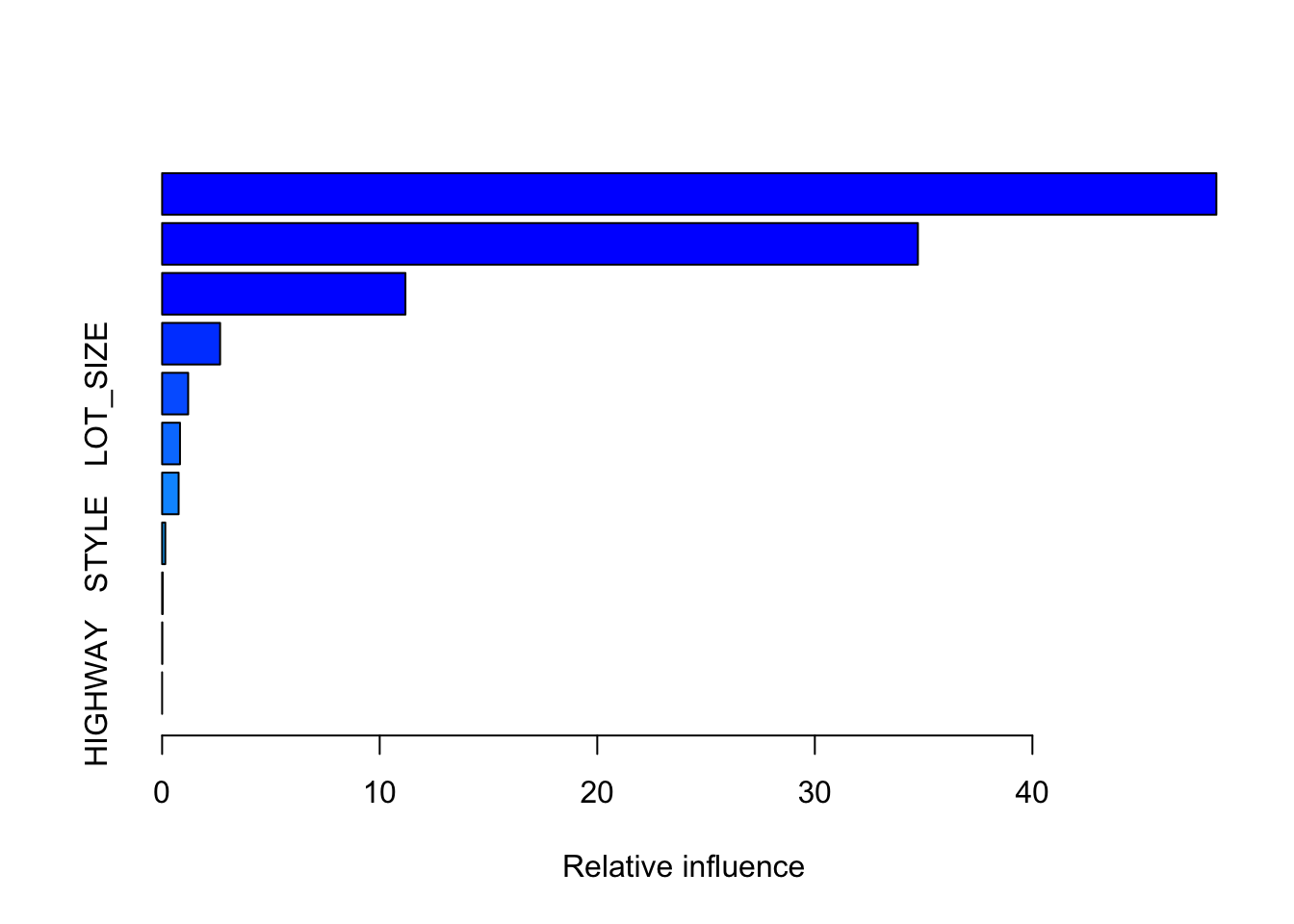

                            var     rel.inf
FINISHED_AREA     FINISHED_AREA 48.45477129
QUALITY                 QUALITY 34.73763114
YEAR_BUILT           YEAR_BUILT 11.18296508
BATHROOMS             BATHROOMS  2.66518029
LOT_SIZE               LOT_SIZE  1.19705485
BEDROOMS               BEDROOMS  0.82130716
GARAGE_SIZE         GARAGE_SIZE  0.75844367
STYLE                     STYLE  0.14509256
AIR_CONDITIONER AIR_CONDITIONER  0.02671275
POOL                       POOL  0.01084121
HIGHWAY                 HIGHWAY  0.00000000
Yhat <- predict(boosth, newdata = homes[-Z,], n.trees = 5000)
mean((Yhat - homes$SALES_PRICE[-Z])^2)^.5
[1] 62831.67

So reducing the shrinkage rate in this case improved the prediction RMSE.

8.10.3.1 Cross Validation for the Number of Trees

We can change the cv.folds= parameter to have it use cross validation for the number of trees.

  • Set the number high.
set.seed(123)
boosth <- gbm(SALES_PRICE ~ . - ID, data = homes[Z,], 
              n.trees = 30000, shrinkage = .001,
              cv.folds = 10,
              distribution = "gaussian")
boosth
gbm(formula = SALES_PRICE ~ . - ID, distribution = "gaussian", 
    data = homes[Z, ], n.trees = 30000, shrinkage = 0.001, cv.folds = 10)
A gradient boosted model with gaussian loss function.
30000 iterations were performed.
The best cross-validation iteration was 22198.
There were 11 predictors of which 10 had non-zero influence.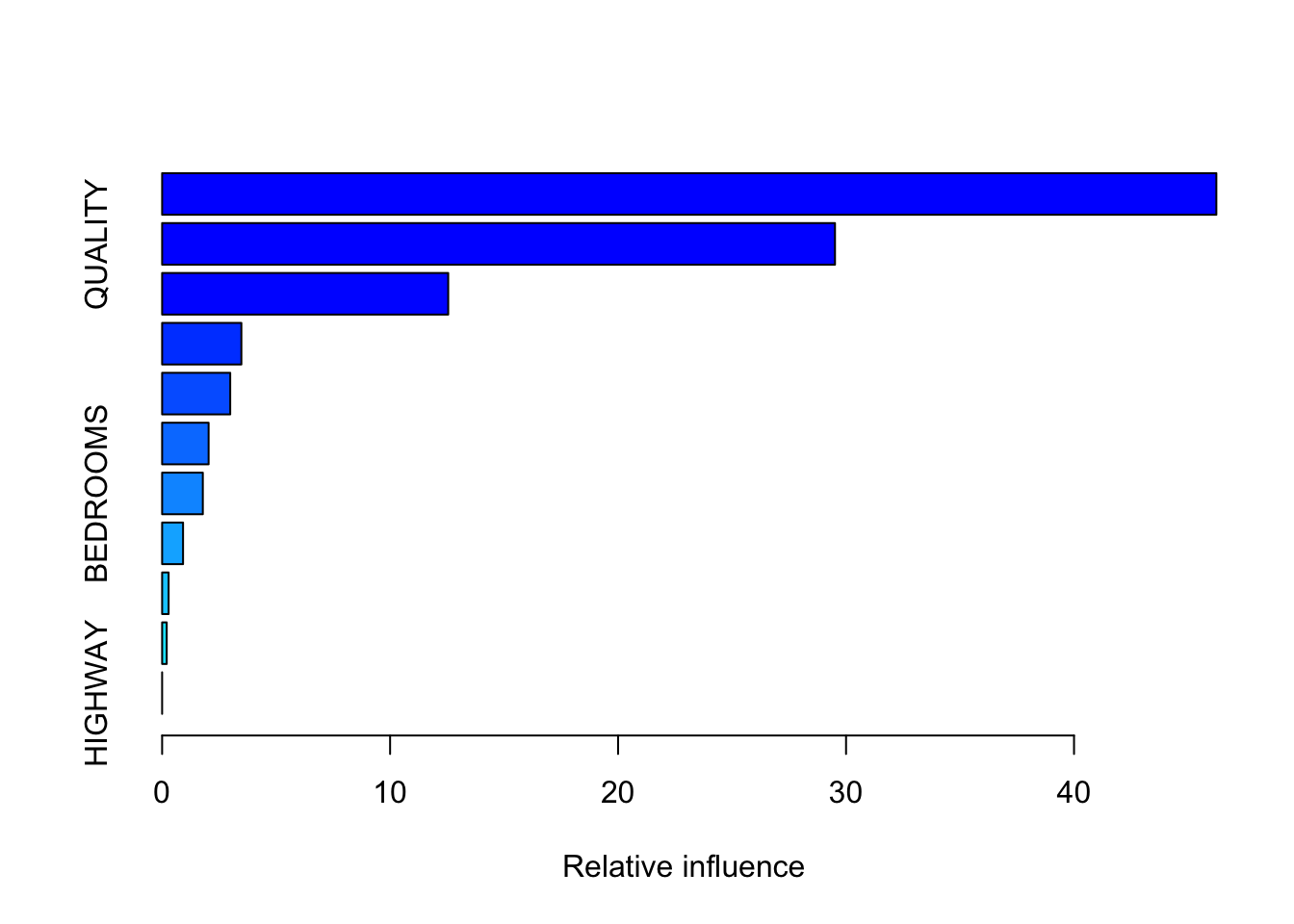
summary(boosth)

                            var    rel.inf
FINISHED_AREA     FINISHED_AREA 46.2432052
QUALITY                 QUALITY 29.5149635
YEAR_BUILT           YEAR_BUILT 12.5490853
LOT_SIZE               LOT_SIZE  3.4763711
BATHROOMS             BATHROOMS  2.9872416
STYLE                     STYLE  2.0391167
BEDROOMS               BEDROOMS  1.7853434
GARAGE_SIZE         GARAGE_SIZE  0.9182208
POOL                       POOL  0.2849619
AIR_CONDITIONER AIR_CONDITIONER  0.2014905
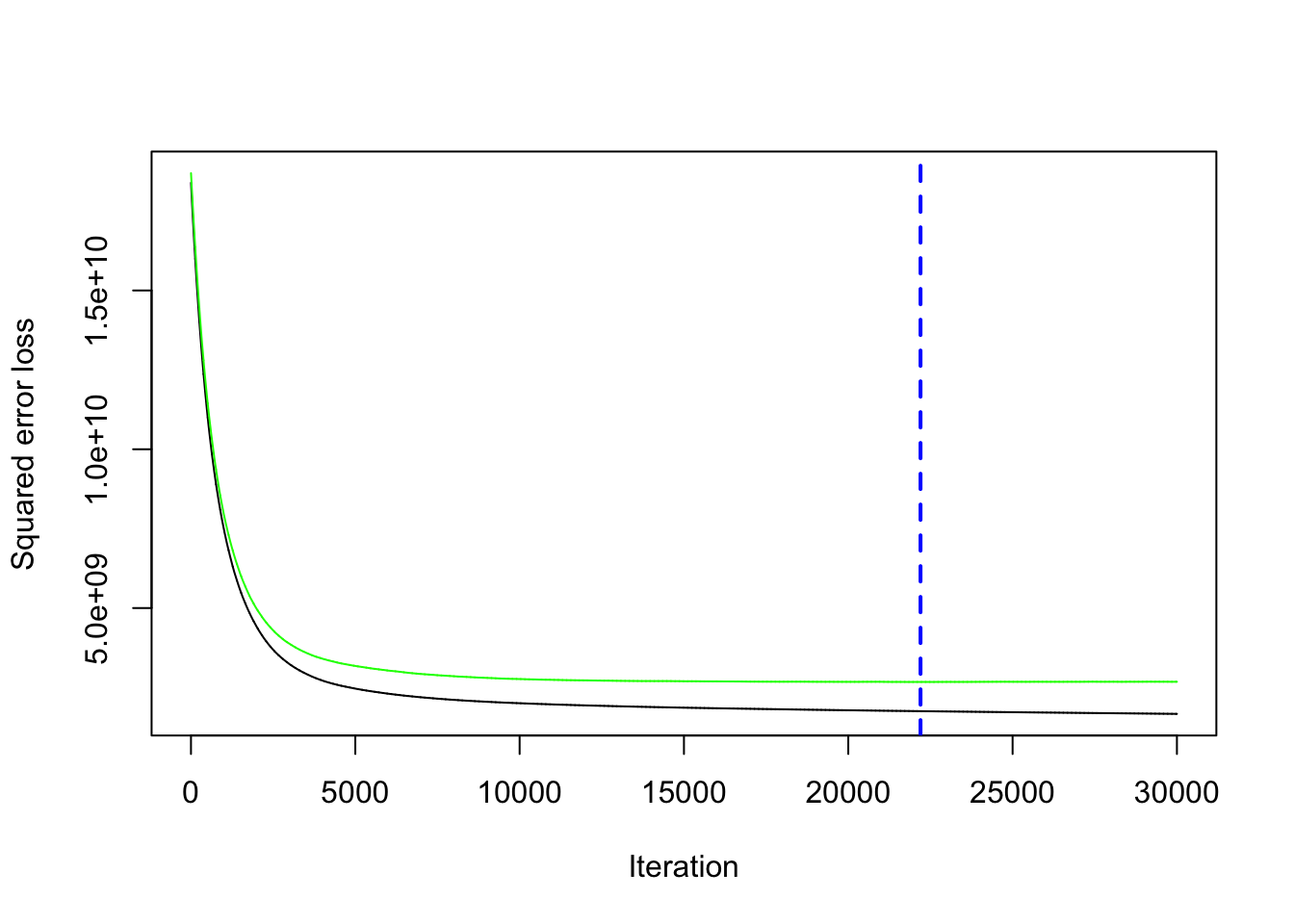
HIGHWAY                 HIGHWAY  0.0000000

The output object now includes a vector of the cross validated error rate (cv.error) for each tree.

  • You can plot the performance for the number of trees with gbm.perf().
  • The black line is the training deviance and the green line is the testing deviance.
  • The tree selected for prediction, indicated by the vertical blue line, is the tree that minimizes the testing error on the cross-validation folds.
  • The smaller you set shrinkage= the more trees you will need.
gbm.perf(boosth, method = "cv")

[1] 22198

Now you can predict on the testing data to calculate MSEP.

  • It will use the optimal number of trees from the output if you used cv.folds greater than 1.
Yhat <- predict(boosth, newdata = homes[-Z,])
mean((Yhat - homes$SALES_PRICE[-Z])^2)^.5
[1] 61032.52

In this case, Random Forests still did better at 60330.43.

You can experiment by making the shrinkage parameter smaller to see how many trees it uses and if it does better on prediction.

Important

Trees provide a relatively explainable approach to regression and classification models.

Trees have a tendency to overfit thus careful pruning or use of Bagging, Random Forests, and Boosting are important methods in developing more accurate and useful models.