Prediction error is equivalent to prediction accuracy – How well can a model predict the unknown.
If we develop a method that has high variance it means there is a lot of noise in the predictions; change the data a little and the results or predictions can change quite a bit.
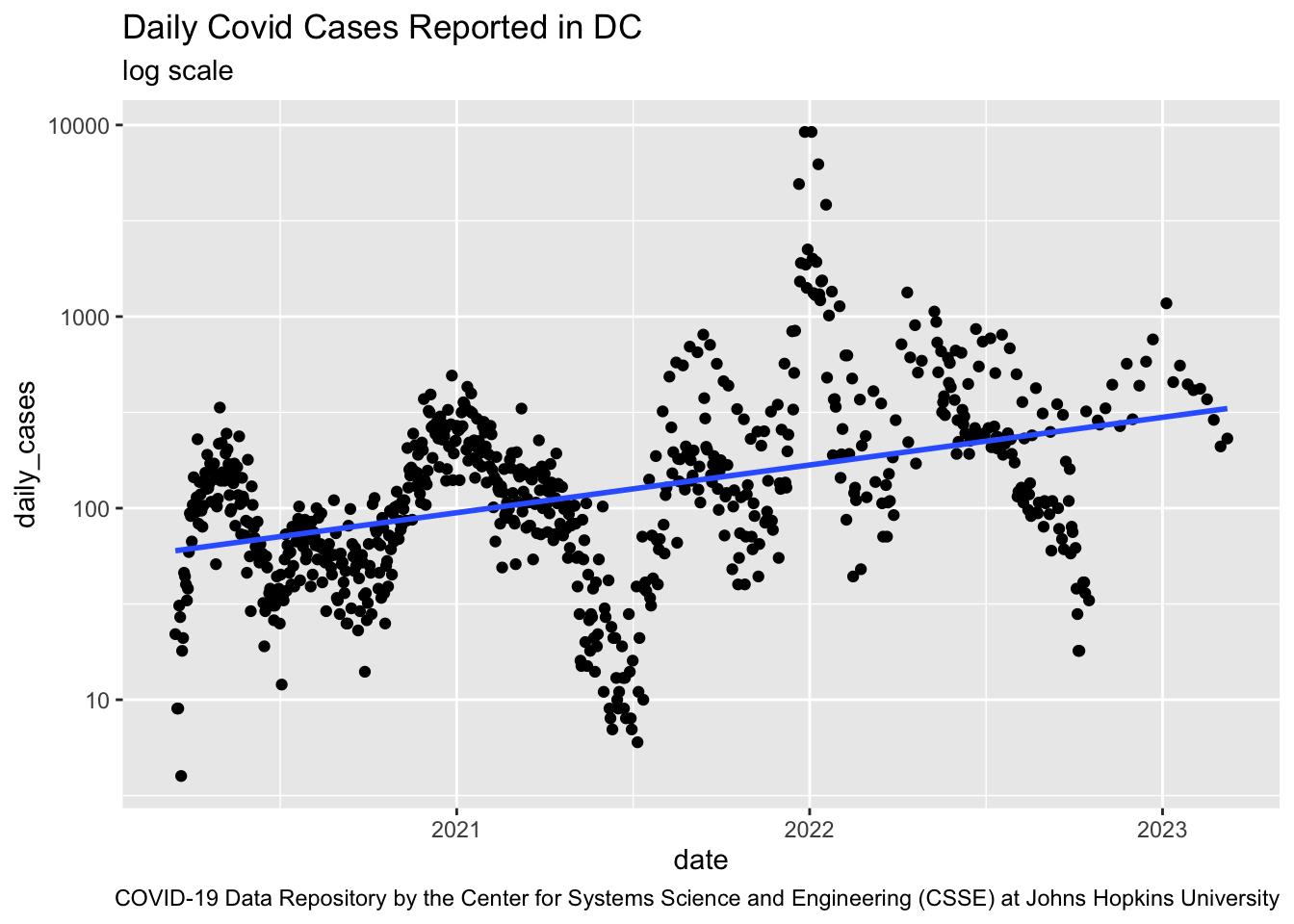
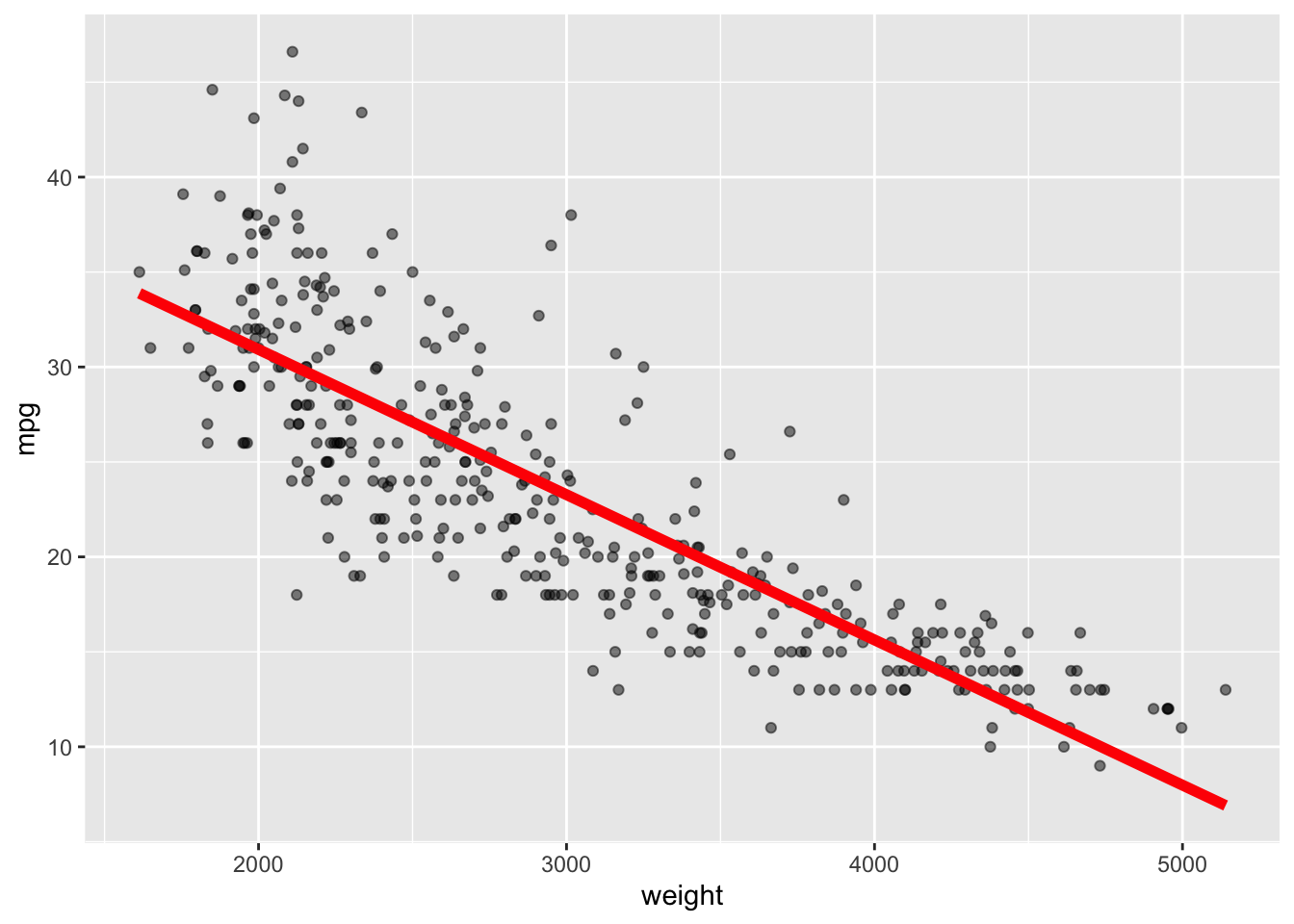
So, in Regression problems when we have a numerical response variable, performance will be measured by prediction mean squared error (MSE) defined as the expected value of the squared residuals:.
Let’s Look at the Elements of MSE
Let’s say we have a regression model where \(y = f(x) + \epsilon\) and
-
\(f\) is some function of \(x\), it could be linear or non-linear.
-
\(\epsilon\) is our error term.
We estimate \(f\) (denoted by \(\hat{f}\)) and if we plug in any vector \(x\) we get the output \(\hat{y}\).
Let’s start with our definition of \(MSE\) from Equation 2.2 and see if we can break it into pieces to better interpret what it means.
\[
\begin{align}
MSE &= E(\hat{y} - y)^2\\
&= E\left(\hat{f}(x) - E\hat{f}(x) + E\hat{f}(x) - Ey + Ey - y\right)^2
\end{align}
\]
Note: \(\hat{f}(x) = \hat{y}\quad\) , \(E\hat{f}(x) = E\hat{y}\quad\) and \(Ey = f(x)\).
Now adding some parentheses we get
\[MSE = E\left((\hat{f}(x) - E\hat{f}(x)) + (E\hat{f}(x) - E(y)) + (E(y) - y)\right)^2
\tag{2.3}\]
- Each of the expectations is non-random – they are not random variables.
- The right-side \(y\) is something new - it’s not in our data set, and
- The left-side predictor \(\hat{y}\) is computed from the data.
Since the right side of Equation 2.3 is outside the data and the left side is in the data, it is reasonable to assume the left-side and right-side of Equation 2.3 are uncorrelated.
Note Equation 2.3 is in the form \((a + b + c)^2\) so it is straightforward to compute:
\[MSE = E(\hat{f}(x) - E\hat{f}(x))^2 + (E\hat{f}(x) - Ey)^2 + E(y - Ey)^2 + \text{combination terms} \tag{2.4}\]
- Since the middle term of \((a + b + c)^2\), (\(b\)), is non-random, we don’t need to take another Expectation.
- The combination terms include \(ab\) or \(bc\) where, since the \(b\) terms are non-random the correlation is \(0\), and \(ac\) which we already said are uncorrelated so the correlation is \(0\).
Removing the combination terms leaves three non-zero terms – the three elements or components of Mean Squared Error.
Let’s look at them starting on the right of Equation 2.4.
\[
MSE = E(\hat{f}(x) - E\hat{f}(x))^2 + (E\hat{f}(x) - Ey)^2 + E(y - Ey)^2
\tag{2.5}\]
What is \(E(y - Ey)^2\) for any random variable? Consider if it were written \(E(y - \mu_y)^2\)?
- It’s the variance of \(Y\) our response variable.
- What can we do about reducing this variance?
- Nothing - it’s the randomness inherent in our response variable’s distribution.
The randomness inherent in our response variable’s distribution* is called the Irreducible Error of MSE since we can’t reduce it.
The other two terms though are based on our data. Together they are called Reducible Error since we can effect them through increasing the size of our data set or using SML techniques and tuning.
If we look at the first term \[E(\hat{f}(x) - E\hat{f}(x))^2 = E(\hat{y} - E\hat{y})^2\] this is the variance of \(\hat{y}\) our predicted value.
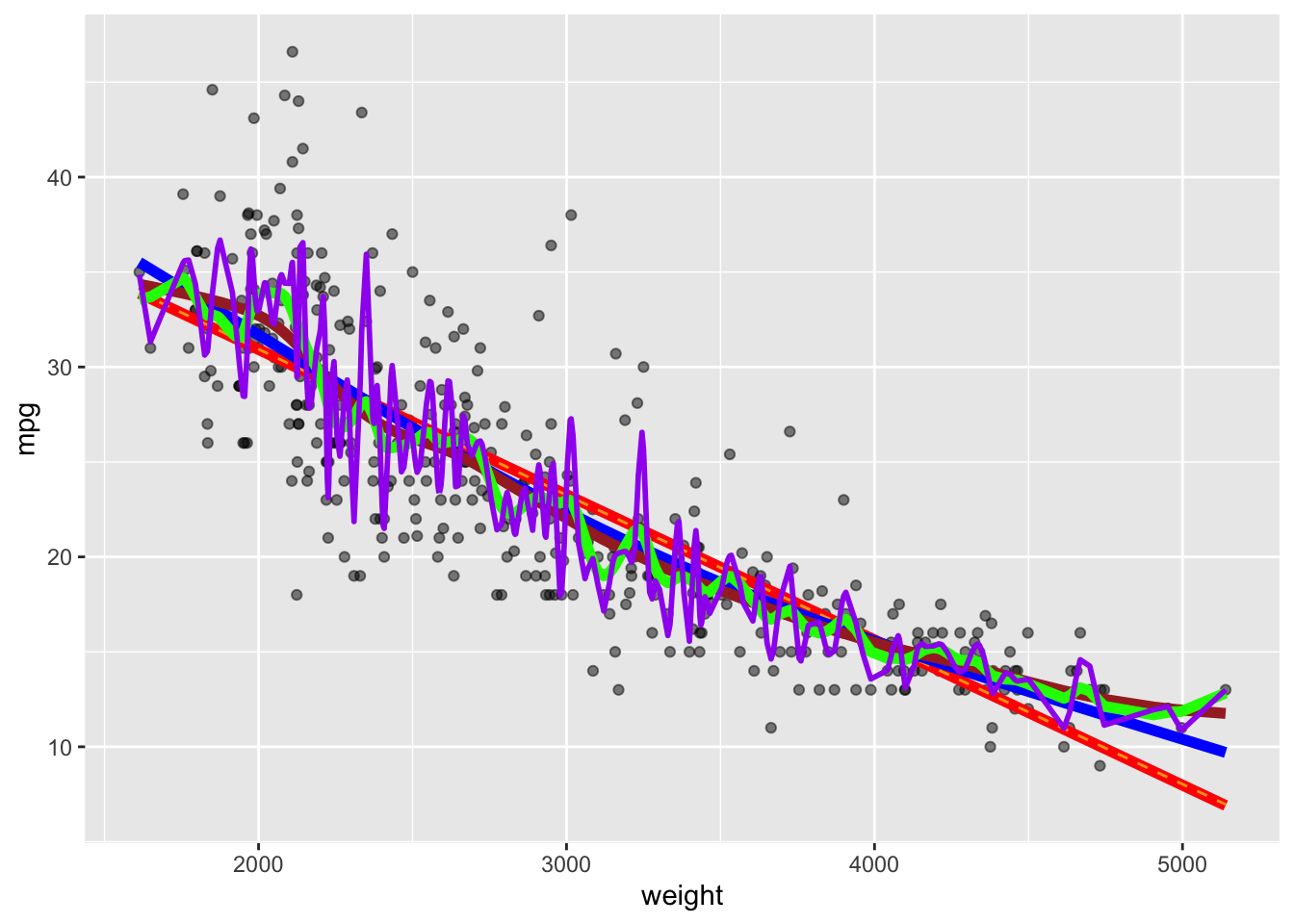
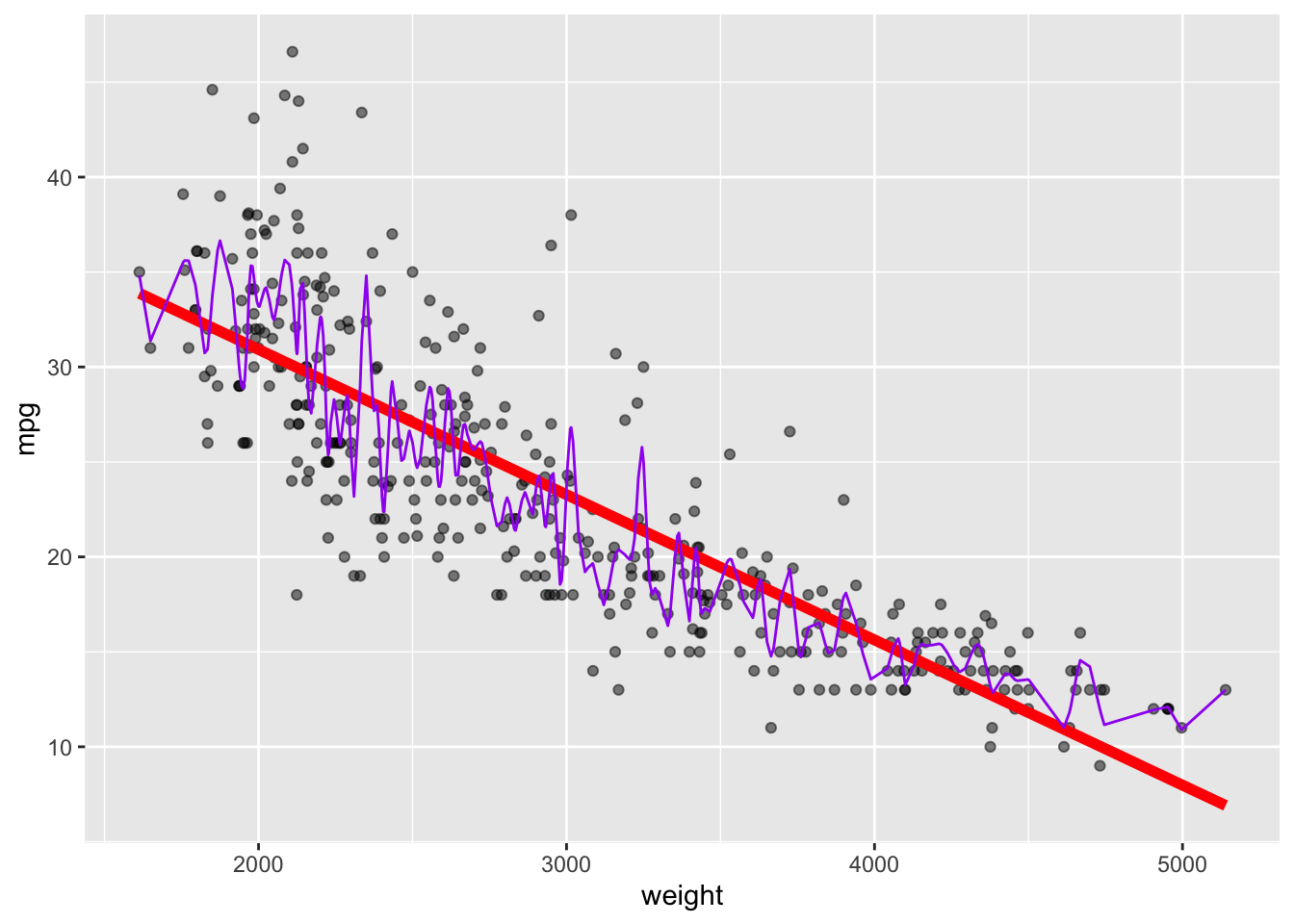
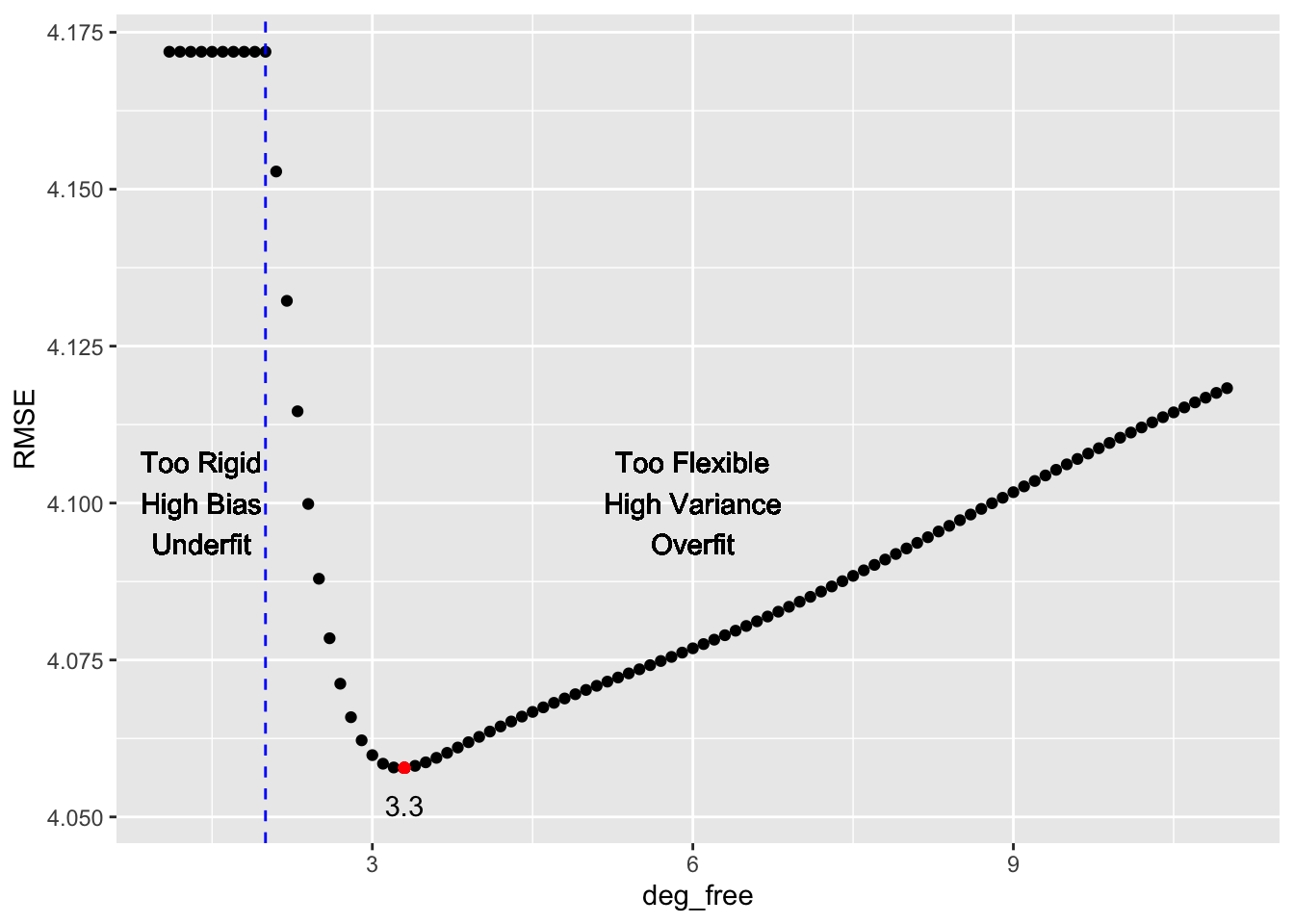
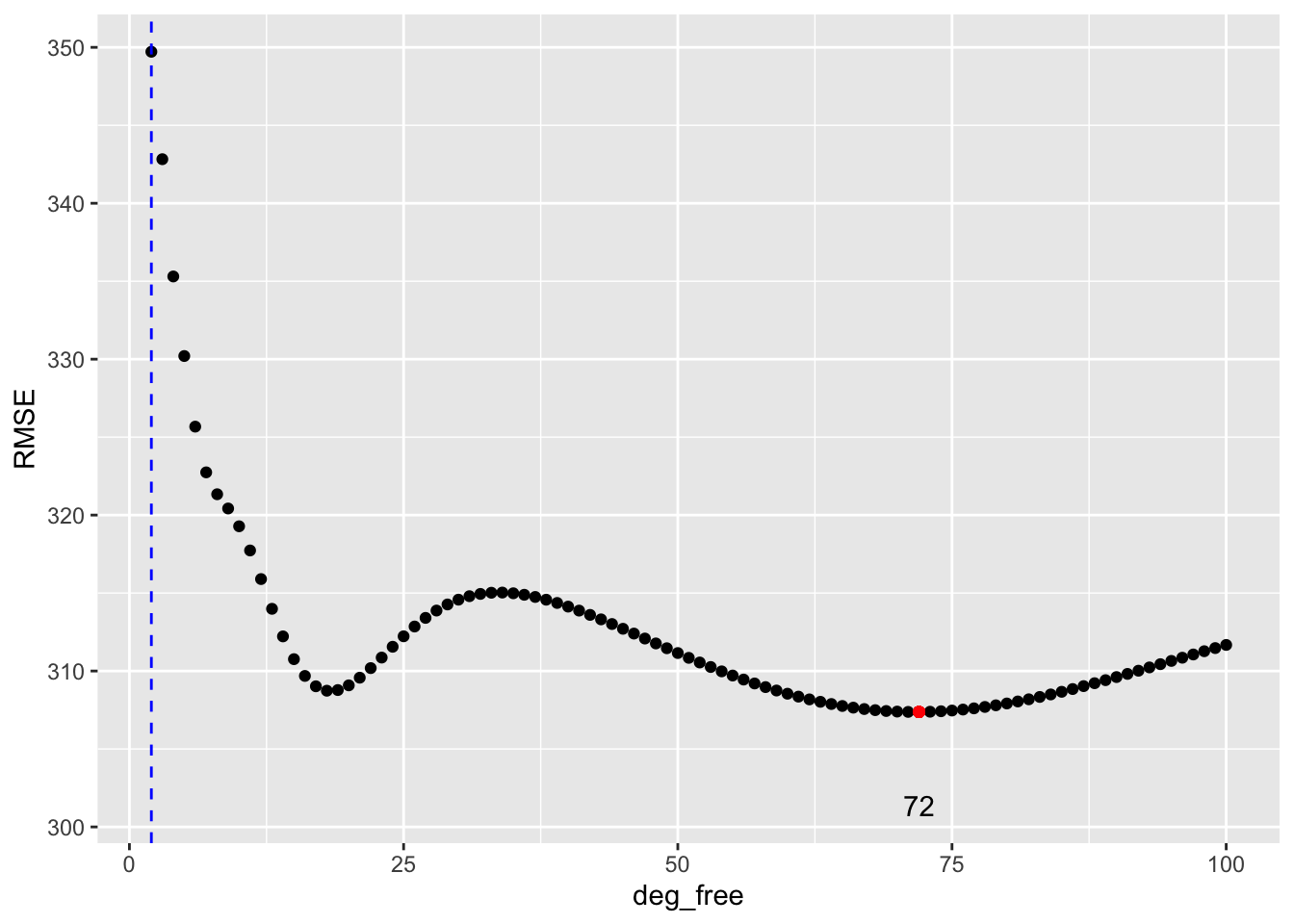
- This is the variance that will increase with a flexible method with many degrees of freedom.
- This is a term we want low.
Let’s look at the middle term \((E\hat{f}(x) - Ey)^2\) which is also reducible.
- Note the right side is \(Ey\) which is the unknown.
- The difference between \(E\hat{f}(x)\) and E\(y\) is the bias of our prediction.
- We want that to be small – to reduce the bias in our estimate.
- If \((E\hat{f}(x) - Ey) = 0\) then our estimated is called unbiased.
- If the difference is not \(0\), then there is bias - our predictions are expected to be too high or too low.
This middle term in Equation 2.5 is the Squared Bias.
- Alf Landon Example: Literary Digest sampled 10-million subscribers and predicted he would win the 1936 presidential election. Their subscribers tended to be wealthier, Republican, and leaning for Landon. Roosevelt won 46 of 48 states.
- MSE is our primary measure of performance for SML models
- MSE has three components:
- Variance of \(\hat{y}\) +
- Squared Bias +
- Irreducible Variance of \(y\)
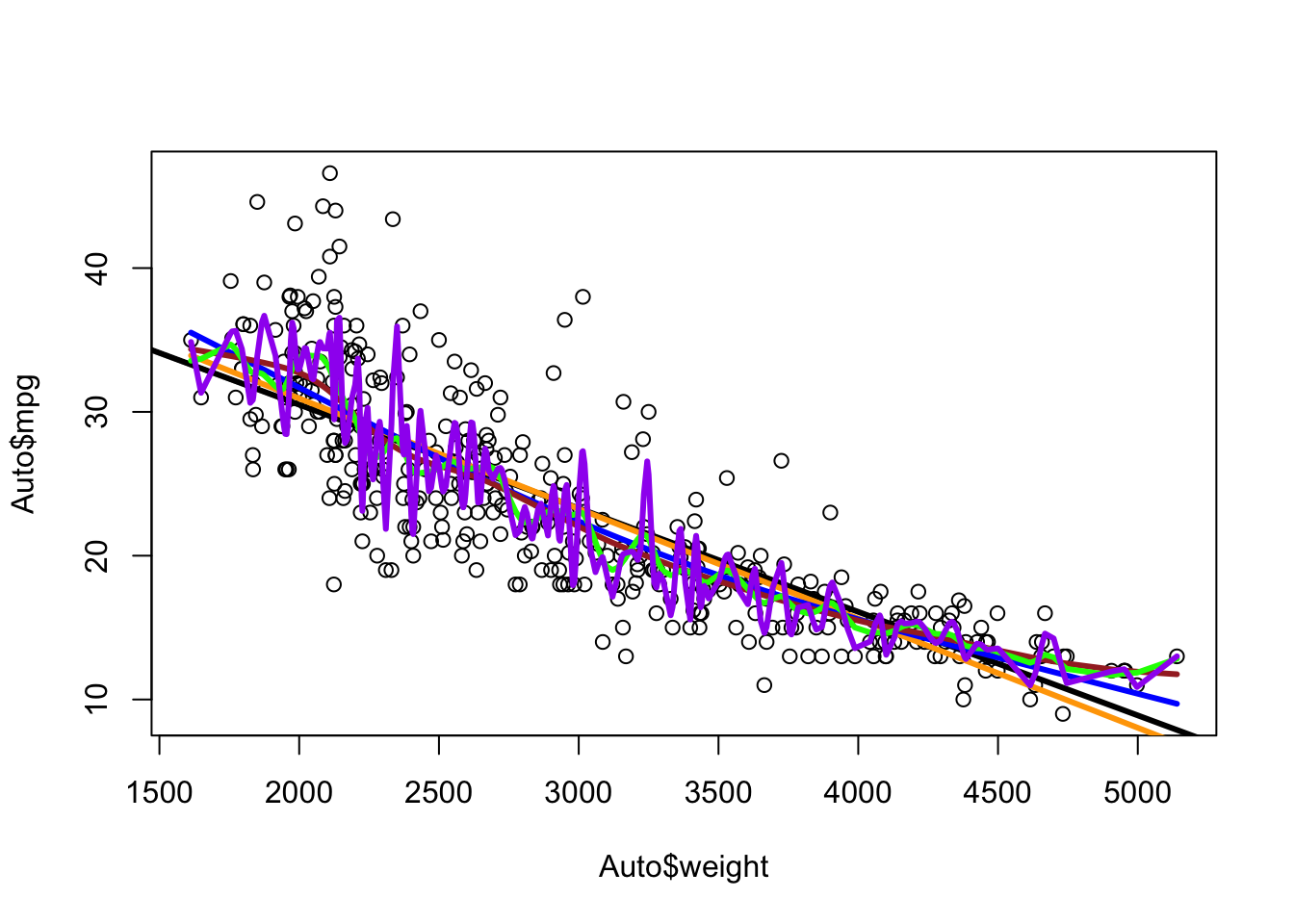
- Flexible Methods have low bias as they can follow the data but can have high variance
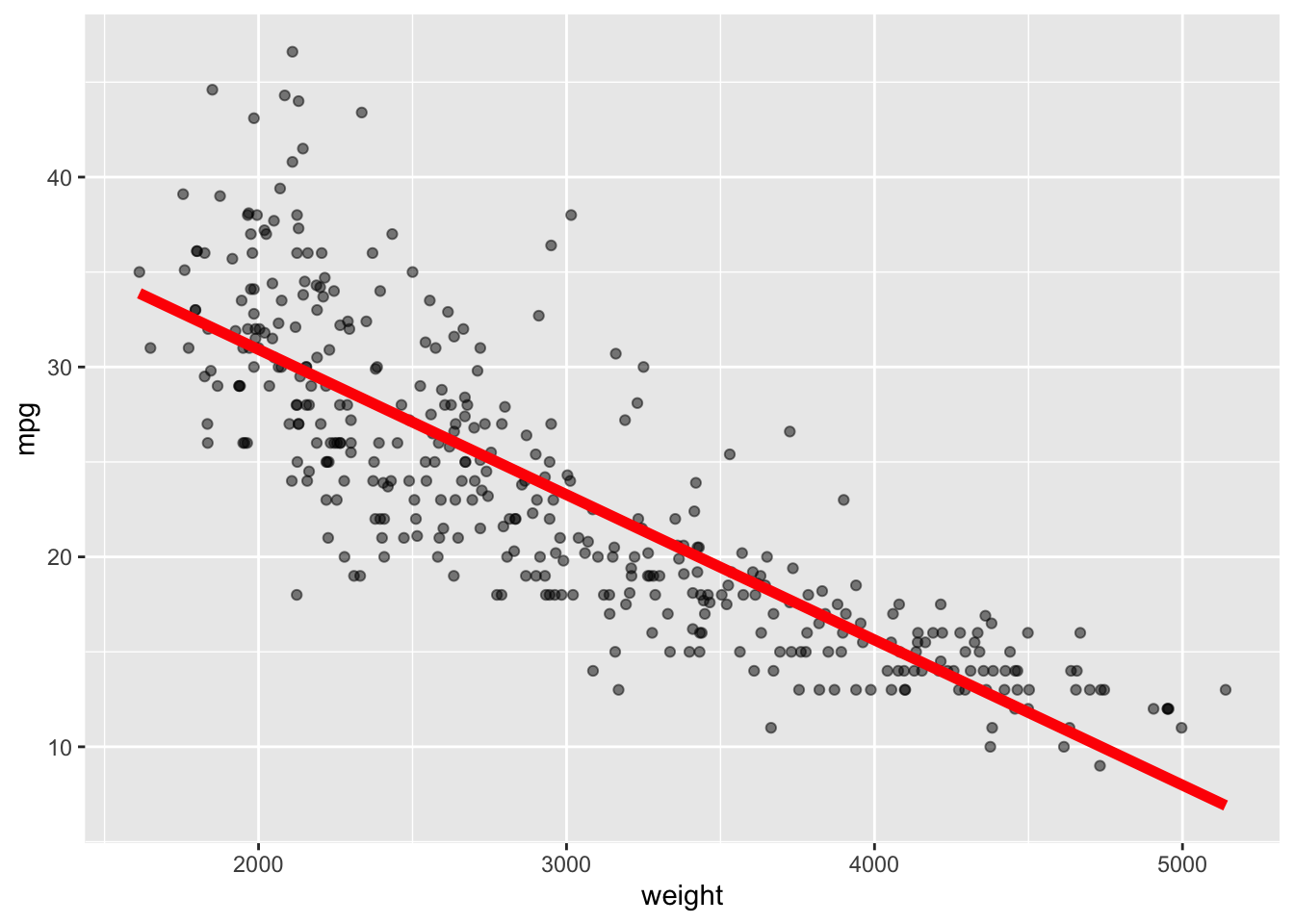
- Restrictive Methods have low variance and high bias as they may not match all the data well.
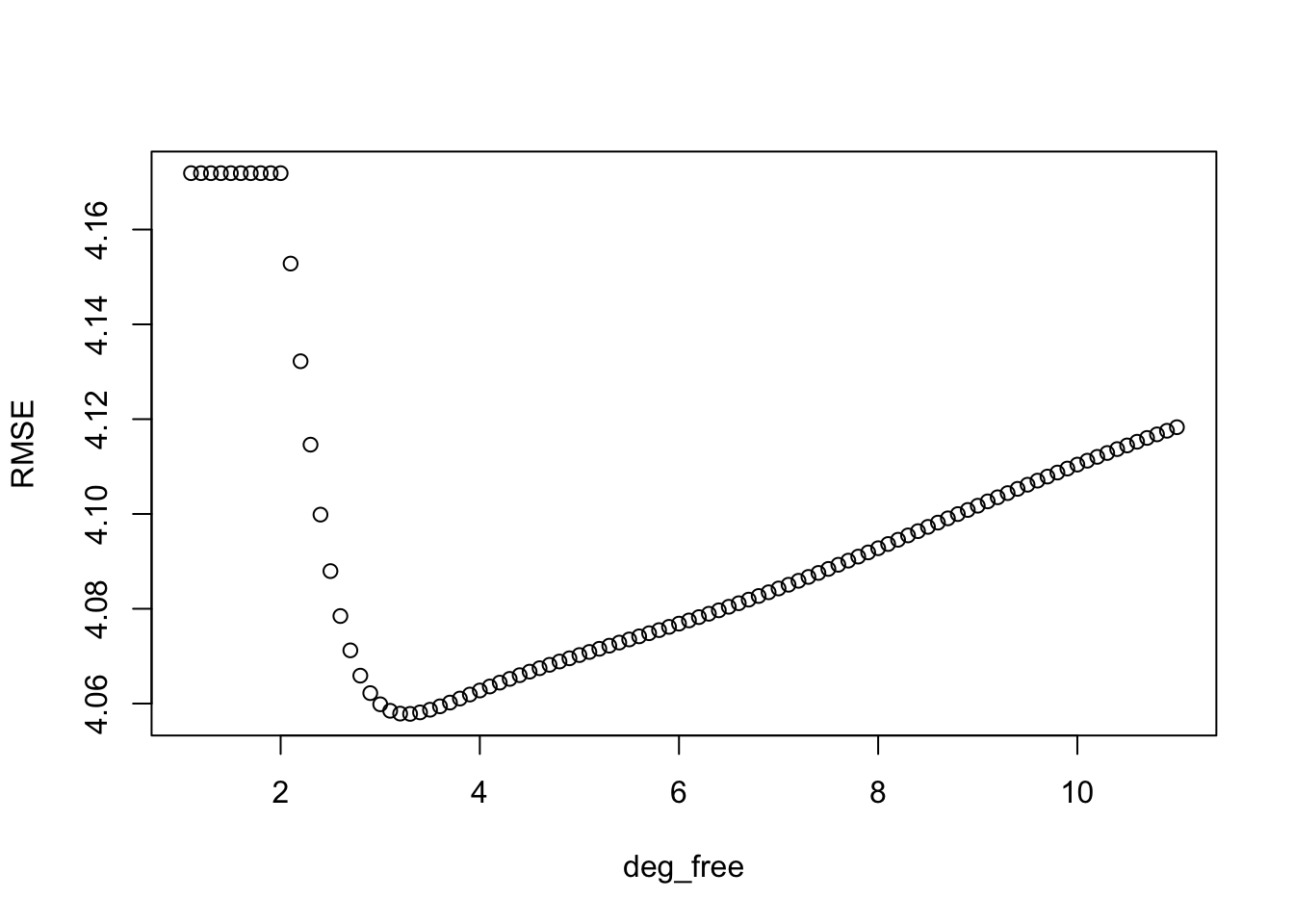
- This need to balance bias and variance in predictions is why SML is not just “plug and chug”– we have to think.
Estimating the MSE
We estimate the MSE for a regression problem by the sample MSE.
\[
MSE = E(\hat{y} - y)^2 \implies \widehat{MSE} = \frac{1}{n}\sum(y_i - \hat{y}_i)^2
\tag{2.6}\]
If we use the entire sample of size \(n\) to estimate the MSE then
\[
\widehat{MSE} = \frac{1}{n}\sum_{1}^n(y_i - \hat{y}_i)^2
\] is called the Training MSE also know as within the sample MSE since the MSE is estimated using the same data used to to fit the model.
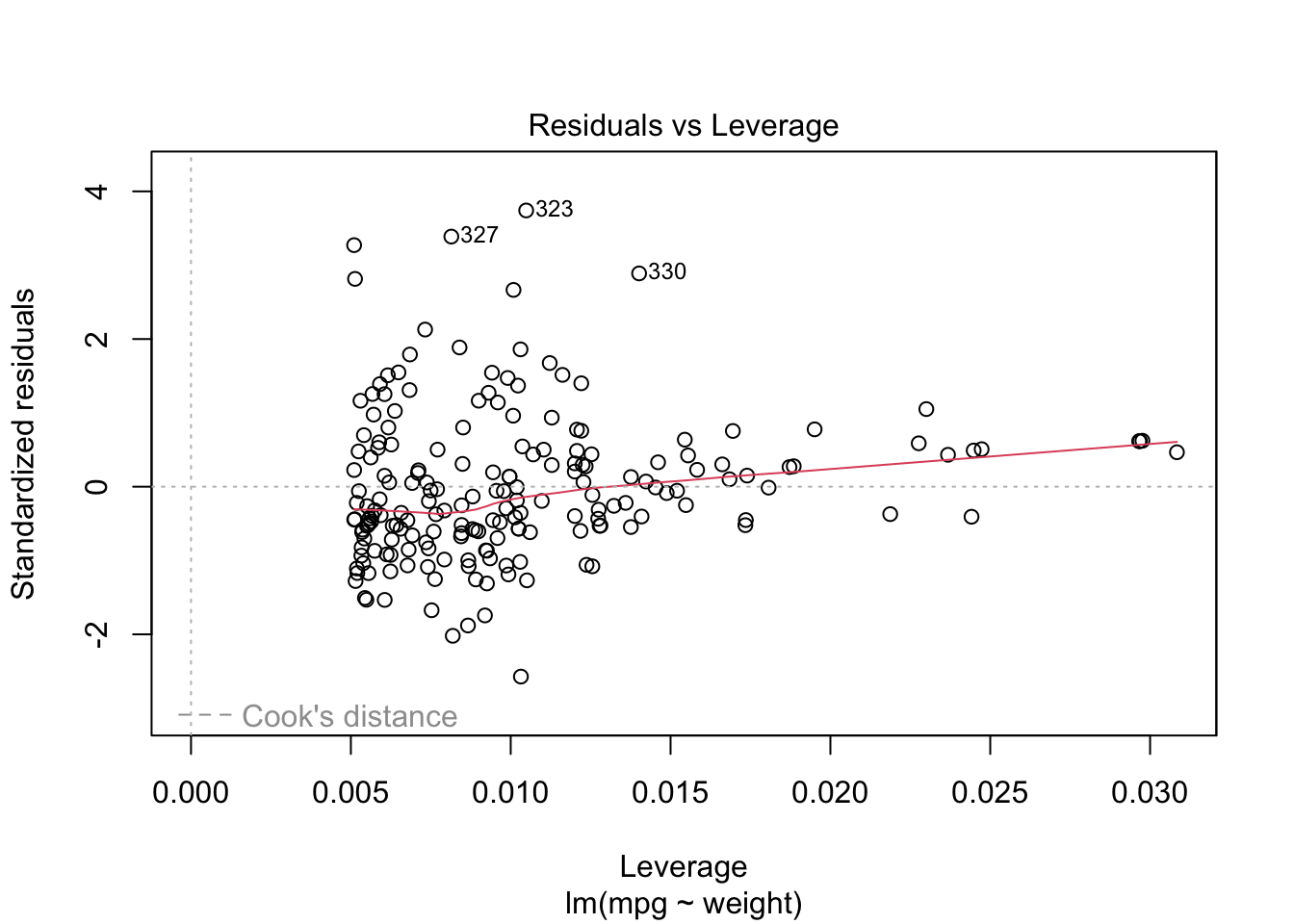
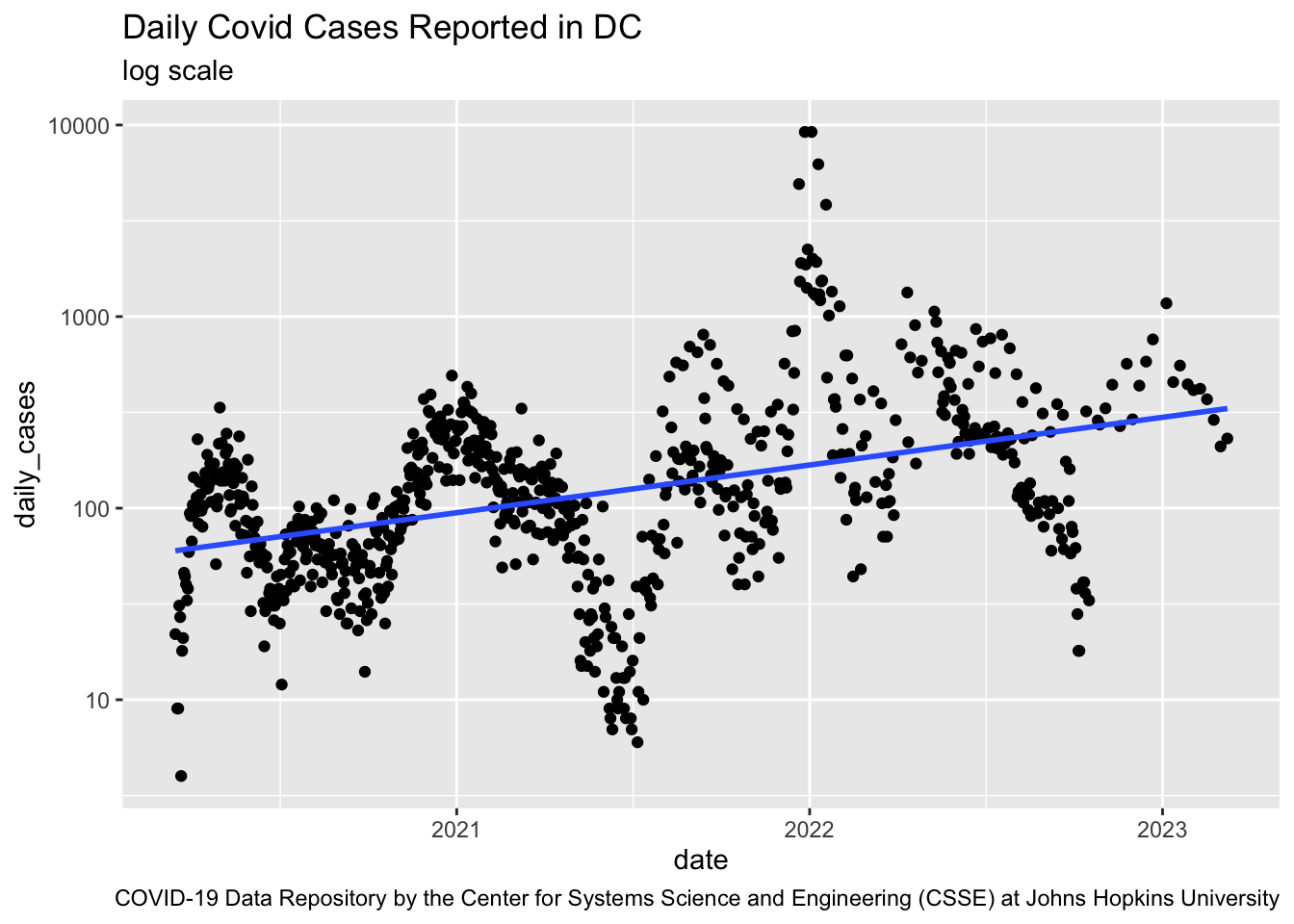
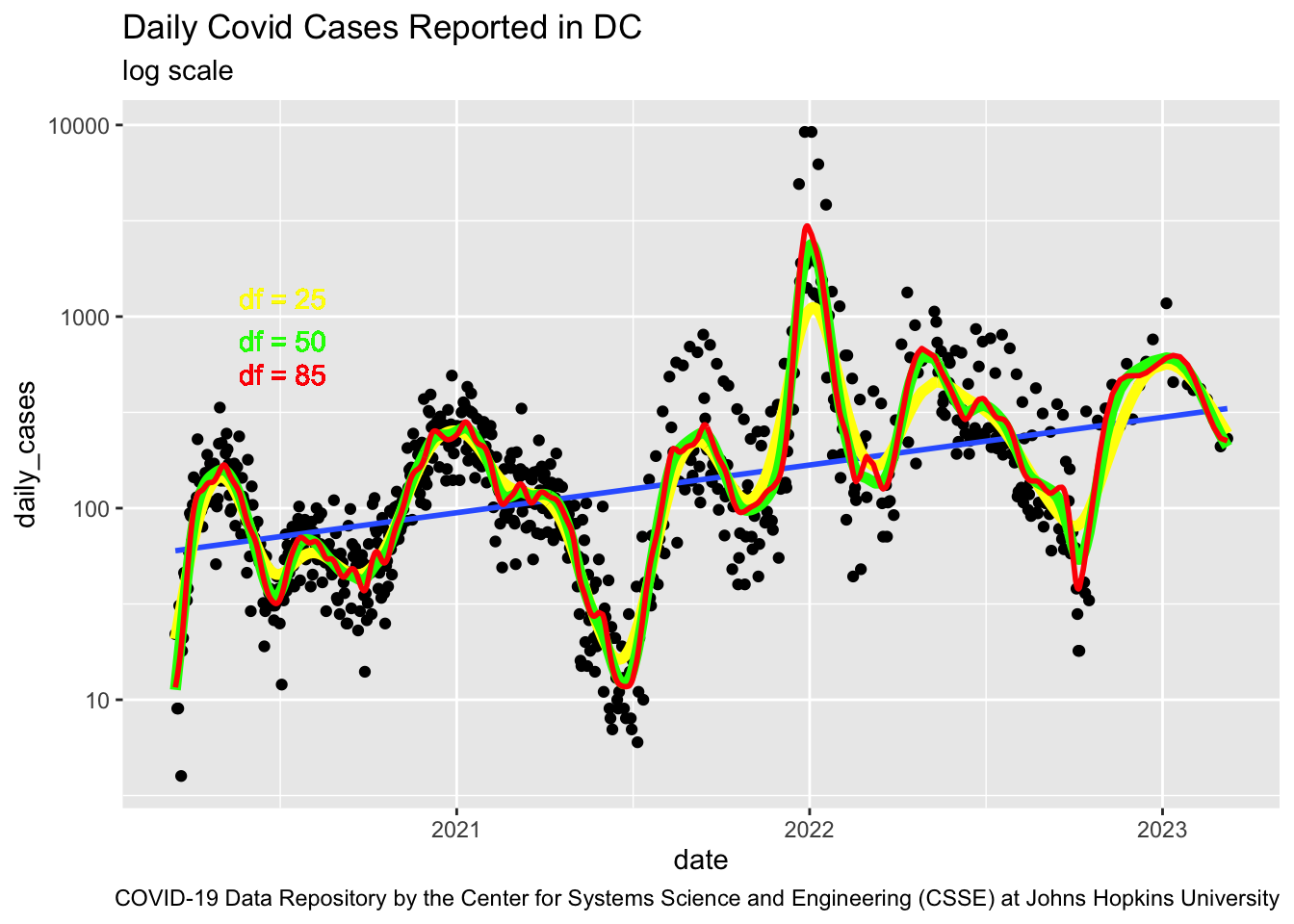
What we really want is the error for our prediction - the Test MSE and it should be estimated from data outside the training sample.
Prediction or Test MSE has to be estimated with data not used to train the model.
How do we do this? We split the data we have.