7 Classification Models

Published

May 23, 2025

Keywords

Categrical Data, Binary Classification, Principal Components Analysis, PCA, k-Means Clustering, Support Vector Machines, SVM, Confusion Matrices

7.1 Introduction

This module teaches some classification methods which are useful for working with response variables that are categorical (factors).

Learning Outcomes

Explain the purpose of classification models.
Explain the difference between regression and binary classification.
Build different classification models: PCA, K-means, SVM,
Tune Classifiers and calculate Performance Metrics
Explain False Positives and False Negatives from a confusion matrix.

7.1.1 References

The R Stats Package. See help("stats").
Support Vector Machines with {e107} Package (Myer 2024)
Another package that does SVM and has data sets is {kernlab} package (Karatzoglou et al. 2024)

7.2 Classification

When your question of interest involves a categorical response, you must use a classification method.

Regression methods/models won’t work with a categorical response very well as they assume the response is continuous.
The will just generate predictions with decimal places and that does not work for things like “hair color” or “gender”.

There are many Classification methods for binary classification (when there are only two levels) or more general approaches for response variable with multiple levels (categories) such as Hair Color.

Consider a dataset containing several variables (columns). Some of the variables are designated as the “response variables” (or “outputs”). You’d like to predict the response variables from the “explanatory variables” (or “inputs”). There are also variables that you didn’t (or couldn’t) measure, which are the “latent variables”.

These distinctions between variable roles are a bit arbitrary, and it can be a bit of a problem to determine which variables should play which role, especially because the same variable can play different roles depending on your research question.

Exploring your data (on the training set, like in Lesson 6) is an important part of determining possible variable roles.

“Machine learning” is a term that you’ve probably heard, perhaps surrounded by a bit of mystery. While there are several different kinds of algorithms that are usually considered “learning”, they are essentially just fancier versions of statistical regression.

Machine learning comes in two varieties: “supervised” and “unsupervised”. In supervised learning, the goal is to predict the response variables from the explanatory ones, given that the training data contains the correct answers, just like traditional regression.
Sometimes you discover new latent variables in the process. In unsupervised learning, the goal is a little different; you want to determine which variables should play which roles.

As in Lesson 6, careful attention to the train-tuning-test process with the data is critical, because modern supervised learning algorithms are extremely flexible.

Moreover, since they are quite a bit more sensitive to the data than (say) linear regression, it is very easy to get a misleading performance measurement if you don’t follow the correct process.

7.2.1 SVM Overview

We’ll focus our attention on one supervised learning classification technique, called support vector machines (SVMs).

The goal of an SVM is simple: given a table of numerical variables, assign a boolean (true/false) classification to each observation.

You use the training sample of your data to help the SVM give the correct classification to a set of observations with known classifications.

Once “trained” you can use the SVM to classify other observations that don’t have known classifications.

For instance, a common task for an SVM might be to determine if a pedestrian is in view of a car’s collision avoidance camera.
Given a digital image – a big collection of numerical variables – the output of such an SVM would simply be “pedestrian” (true) or “not pedestrian” (false).

A given SVM is a rather elaborate algorithm, whose behavior is determined by quite a few numerical “parameters”.

The training data are used internally to determine these parameters.
Thankfully, that process is handled internally by the {e1071} package, so you can just tell an SVM to “train thyself” given some data and it will!

Actually, there are many kinds of SVMs, though they ultimately look about the same to the data scientist from the standpoint of inputs and outputs.

The {e1071} library provides four different types of SVM, though there are many others that are in wide usage.
In the machine learning jargon, this means that in addition to the parameters of each SVM, there are “hyperparameters” that select the particular SVM algorithm you want to use.

In our train-tuning-test process, the tuning stage, where we select one algorithm without changing it, can be thought of as the training stage for the hyperparameters.

It sounds fancy, but it’s really pretty easy: try a handful of versions of your algorithm, and then pick the best.

library(tidyverse)
library(e1071)

It you get an error, you probably do not have the e1071 library installed, and you’ll need kernlab for our dataset. Here is how to fix that:

install.packages('e1071')
install.packages('kernlab')

7.2.2 The `spam` data set

The data we’ll be using for this lesson is kind of amusing

data("spam", package = "kernlab")

It is a single table, called spam, in which each row corresponds to an email message.

The columns are normalized word frequencies for various words present in the textual content of the messages.
Finally, there is a type column that either contains the string “spam” or “nonspam”.

You guessed it! We are going to make an email spam filter!

Now it happens that this particular dataset is rather easy to “cheat” because it includes a few oddities in how it was collected.

Specifically, this dataset was collected before “spear phishing” was common (where a spammer impersonates a trusted sender whose account has been compromised).
As a result, words that are characteristic of the data collector’s organization are a dead giveaway that a message is “nonspam”.
These correspond to two columns: george and num650, so we’ll deselect these.

7.3 Create Validation Sets

As we described earlier, we need to create a sampling frame and split our data into training, tuning, and test sets.

set.seed(1234)
raw_data_samplingframe <- spam |>
  select(-george, -num650) |> # Remove the "cheating" columns...
  mutate(snum = sample.int(n(), n()) / n())

training <- raw_data_samplingframe |>
  filter(snum < 0.6) |>
  select(-snum)

tuning <- raw_data_samplingframe |>
  filter(snum >= 0.6, snum < 0.8) |>
  select(-snum)

test <- raw_data_samplingframe |>
  filter(snum >= 0.8) |>
  select(-snum)

You can save these off in CSV files if you like.

training |> write_csv("./output/spam_training.csv")
tuning |> write_csv("./output/spam_tuning.csv")
test |> write_csv("./output/spam_test.csv")

In a few places we will want just the input variables. It will be frequently useful to have the correct answers in a separate table as well.

Let’s split these off now:

training_input <- training |> select(-type)
training_truth <- training$type

tuning_input <- tuning |> select(-type)
tuning_truth <- tuning$type

test_input <- test |> select(-type)
test_truth <- test$type

7.4 Training stage:

7.4.1 Principal Components Analysis

Let’s start with a quick visualization! Since all the explanatory variables are numerical (they’re normalized word frequencies) and there are quite few of them, principal components analysis (PCA) is a good way to create just two variables that contain most of the information in the data.

Note

Principal Components Analysis (PCA) is a well-established method for reducing the dimensions of the data.

It uses linear algebra to create linear combinations of a set of \(k\) variables into \(k\) Principal Components where each principal component is independent of the others.

The Principal Components are designed so the First principal component captures as much information as possible from one linear combination, then the second captures the most of out what is left, and so on.

Thus the first two principal components are often used in plots as they capture the bulk of the information in just two variables so we can easily plot them.

Use the prcomp() function from the Base R {stats} package.

spam_pca <- training_input |> prcomp()

Now we can plot the messages as a scatterplot, and color by type:

spam_pca$x |>
  as_tibble() |>
  mutate(type = training_truth) |>
  ggplot(aes(PC1, PC2, color = type)) +
  geom_point()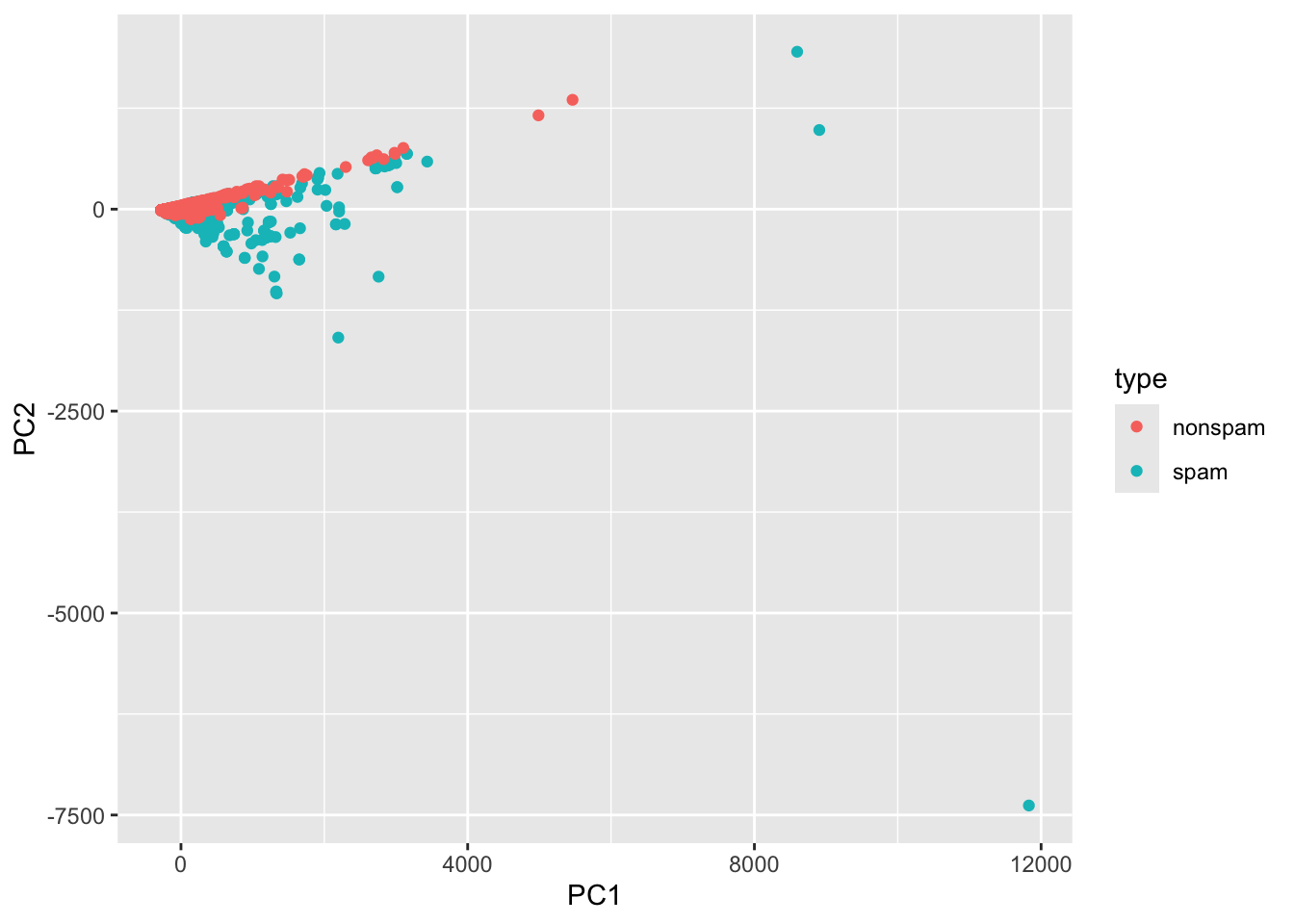

Each message corresponds to a point in this plot.

Messages with similar word usage end up near each other, while messages using different words tend to be further away from each other.
Notice how the spam messages spread out a bit further from the nonspam messages.
These outliers are easier to detect than the spam messages that do a better job of looking like a nonspam message.

7.4.2 K-Means Clustering

Clustering with k-means is a kind of “semi”-supervised learning, in that we tell it the number of classes we want.

Note

K-means clustering is a method for separating data into \(k\) clusters or groups (you pick the \(k\)) such the points in each cluster as as similar to each other as possible and as dissimilar to points in any other cluster as much as possible.

K-means is an iterative algorithm.

We set the seed as the first step in K-means is to randomly assign all points to one of the possible clusters.
It then calculates a lot of distances and moves points from one cluster to another.
It then recalculates the distances and moves points, over and over, until the improvement in performance is minimal.

In the case of spam detection, there are two classes: spam and nonspam. So, here we go!

Use the kmeans() function from the Base R {stats} package.

set.seed(1234)
spam_kmeans <- training_input |> kmeans(2)

Did k-means correctly identify the spam? We can tell if we make a table comparing the k-means cluster ID (an integer) with the true classes:

kmeans_results <- tibble(training_truth, km = spam_kmeans$cluster)

Then we can count the number of times we get a match between the two.

We could use table() but I think this looks nicer as a contingency table, so we’ll need to pivot_wider():

table(kmeans_results)
kmeans_results |>
  count(training_truth, km) |>
  pivot_wider(names_from = km, values_from = n)

              km
training_truth    1    2
       nonspam 1675   31
       spam     946  108

# A tibble: 2 × 3
  training_truth   `1`   `2`
  <fct>          <int> <int>
1 nonspam         1675    31
2 spam             946   108

Have a look at the results closely.

The best possible performance consists of having each row and each column having exactly one zero entry.
Because k-means has an element of randomness to it, I can’t tell you specifically which class ID number (the km column) means spam or not, but it’s not very effective.

Just as a sanity check, though, you can ask whether k-means is detecting “something” about the spamminess of a message.

The way to do this is with chi-squared.
We’ve done this many times before, so the following block of code should make perfect sense to set up the contingency table:

ct <- kmeans_results |>
  count(training_truth, km) |>
  pivot_wider(names_from = km, values_from = n) |>
  column_to_rownames("training_truth") # Look out! column named the same as a variable!

And then let’s just run the test:

chisq.test(ct)


    Pearson's Chi-squared test with Yates' continuity correction

data:  ct
X-squared = 95.041, df = 1, p-value < 2.2e-16

Well, I got a small \(p\)-value. So k-means detects a statistically significant feature of the spam, but it’s not really conclusive either.

Why did k-means do poorly? Let’s label the PCA plot we made in Step 8 with the k-means clusters instead of the true values:

We use as.factor() to convert the clusters from numbers to a factor so the legend is correct.

spam_pca$x |>
  as_tibble() |>
  ggplot(aes(PC1, PC2, color = as.factor(spam_kmeans$cluster))) +
  geom_point(alpha = .6)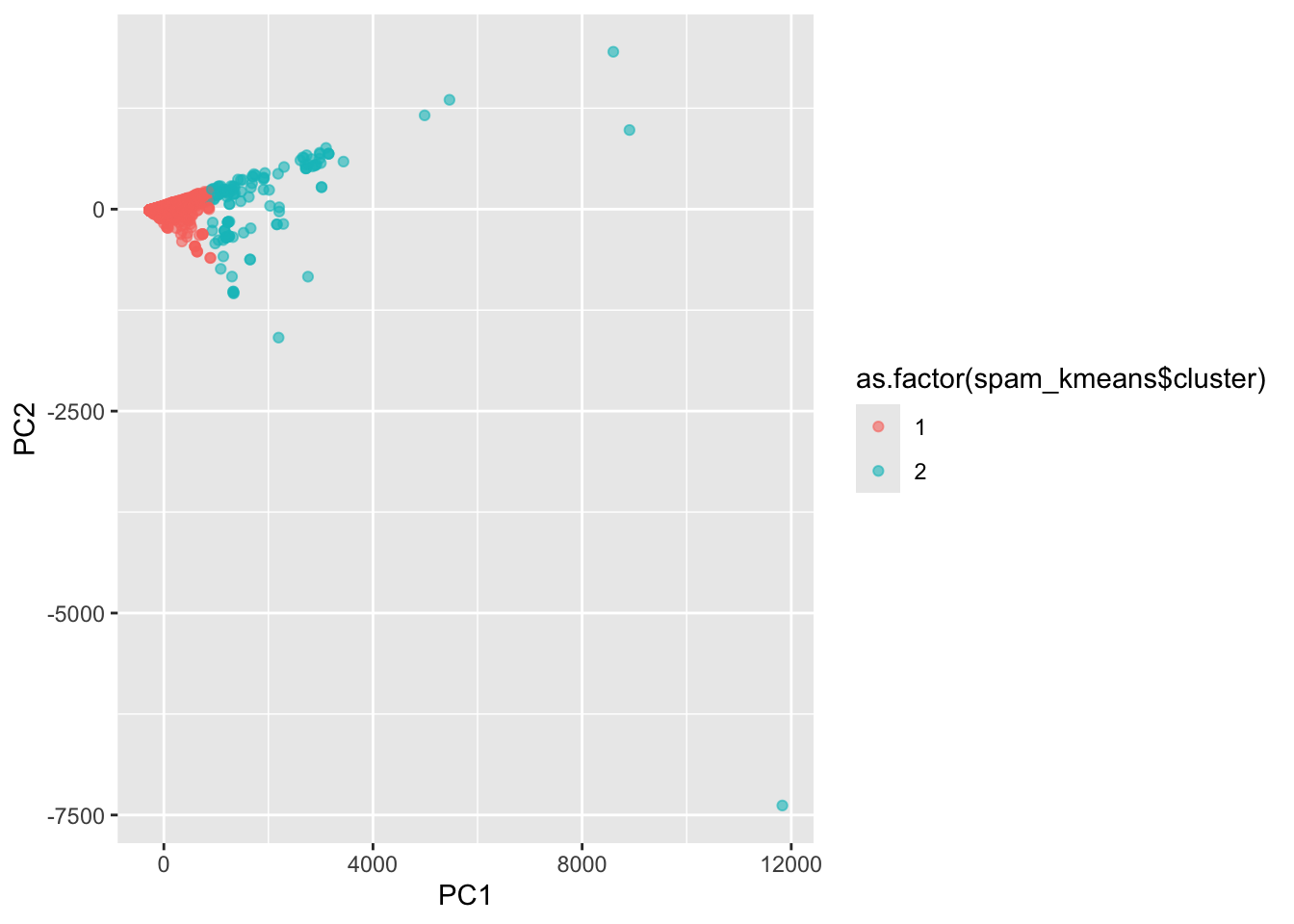

What you should see is that k-means splits the messages into an “inner core” and “outliers”.

It labels all of the inner core as nonspam, and the outliers as spam.
While this works for the really far outliers (which are obviously spam messages!), it doesn’t do a good job closer to the core.

Let’s give up on k-means, and switch over to SVM training.

7.4.3 Training the SVM

You train an SVM using the svm() function.

The svm() function can take two styles of input, though they both do the same thing internally. If you’re interested, you can read the documentation:

?svm

Here’s the format that the e1071 authors use more frequently in the documentation:

The ~ is the formula operator again.
The . on the right side of the ~ means use all the variables.

svm_linear <- svm(type ~ ., # Watch the syntax.  It's a tilde, a period, and then comma
  data = training, # Unlike tidyverse, the data input is not the first argument.  We can't pipe...
  kernel = "linear"
) # "linear" is the hyperparameter (see Step 14)

The other option is tidyverse compatible, but you have to split the data into input and output first:

svm_linear <- training_input |>
  svm(y = training_truth, kernel = "linear")

These both do the same thing, so pick whichever you like. I’m going to use the first version in what follows.

The way SVMs work is that they split the space of observations (imagine the PCA plot) into two halves by way of a “separating surface”.

That surface is high dimensional and takes quite a few parameters to define, but you need not worry too much about them.
Additionally, there are many kinds of surfaces you might try to use, each defined by a set of equations. - Choose a different set of equations, and your surfaces will look different!
The choice of a set of equations is called a “hyperparameter”, and in the case of svm(), the hyperparameter is called kernel.

There are four kernels supported by e1071:

‘linear’ : The separating surface is a flat plane
‘polynomial’ : The separating surface is a given by a polynomial… like \(z=ax^2+by^2+cxy+...\) (lots more)
‘radial’ : The separating surface is an ellipsoidal blob
‘sigmoid’ : The separating surface is kind of “S”-shaped

Since our dataset isn’t too big, it doesn’t hurt to try all of these!

We can use the tuning dataset to select the one that does the best job at correctly classifying the email messages as spam or nonspam.

How do we do this? Well, we just repeat with a different kernel:

svm_poly <- svm(type ~ .,
  data = training,
  kernel = "polynomial"
)
svm_radial <- svm(type ~ .,
  data = training,
  kernel = "radial"
)
svm_sigmoid <- svm(type ~ .,
  data = training,
  kernel = "sigmoid"
)

Note: each of the different kernels have additional hyperparameters in them (like degree, gamma, and the like), that you might need to change in some circumstances. - We don’t need to do that here, but you may have to change them if you don’t get good results on other data…

Now that we’ve trained the SVMs for our data, it’s a good idea to anticipate their performance.

7.4.4 Plotting Results

Plotting is perhaps the best way to do this, but plotting in the original data variables is not reasonable.

That’s unfortunate because that’s how our SVMs were trained.
But, since we are using the training data, there is nothing wrong with training an additional set of SVMs to work on the PCA data since these plot better.
The hope (which will be validated against the tuning sample) is that these plots will be representative.

To that end, we need to transform the training data using PCA, and add back the true classifications (‘spam’ / ‘nonspam’).

training_pca <- spam_pca$x |>
  as_tibble() |>
  mutate(type = training_truth)

OK, let’s plot each SVM. It happens that the trained SVMs made by the svm() function already know how to plot themselves, though this doesn’t use ggplot().

Instead, it uses the base R plot() function. Here’s how to do it:

sl <- svm(type ~ ., data = training_pca, kernel = "linear") # Watch the punctuation!
plot(sl, training_pca, PC1 ~ PC2, grid = 400) # This plots PC1 versus PC2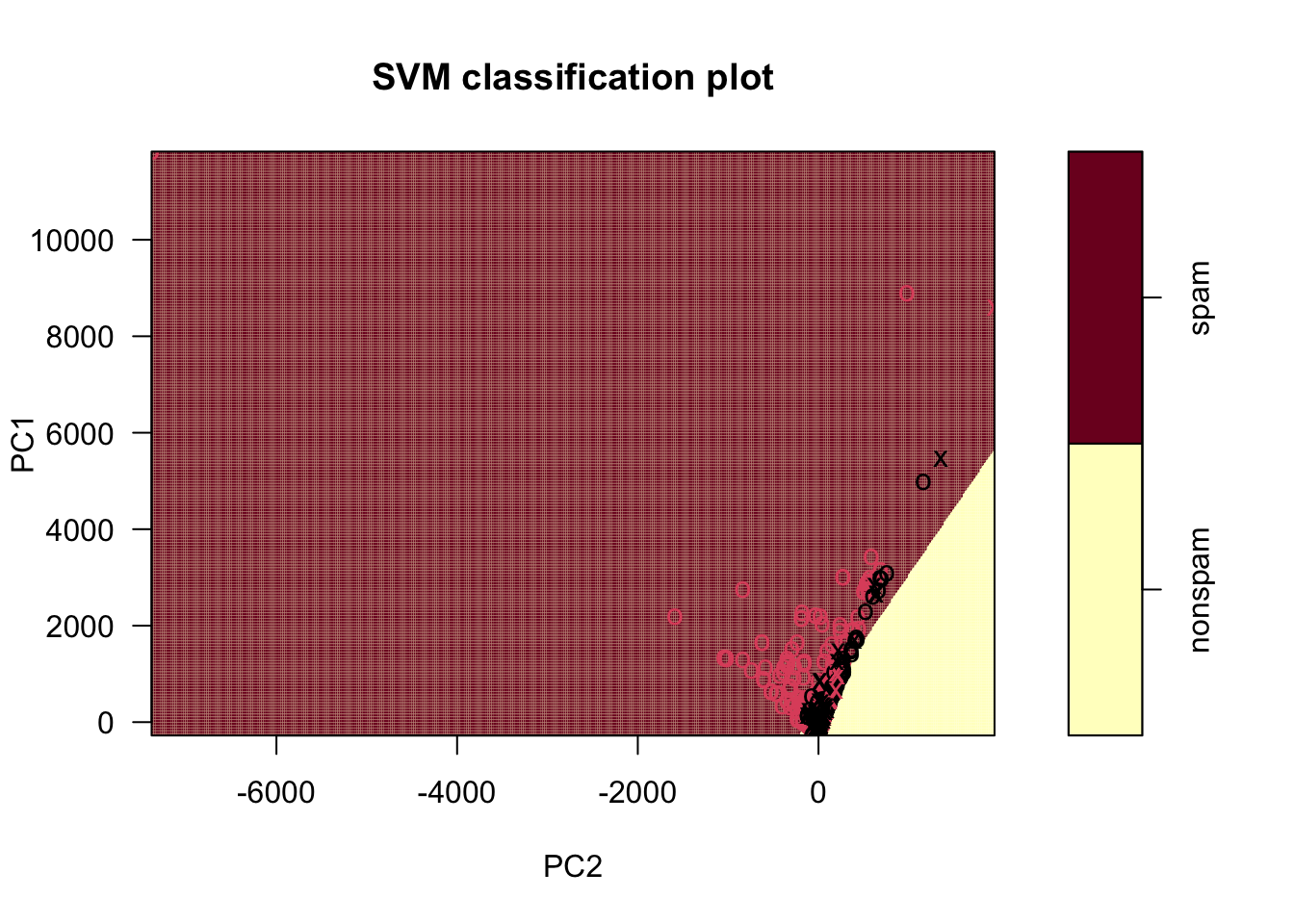

The points are color coded according to the actual response.
The x shapes are the points that are the “support vectors” used to figure out the boundary.
The black points in the red space are misclassified

If you look closely at this, you can see a line slicing through the plot, separating the spam from the nonspam. It does a pretty good job!

Try this with the other three kernels, changing what evidently needs to be changed.

Notice the different shapes of the different spam/nonspam regions! They all look a little different.

Which do you think best matches the shape of the true classes?

7.5 Tuning stage

Now we’re ready to choose the SVM kernel that will serve as our final version! Since our SVMs are already trained, we can just apply them to the new input data.

The way to do this is via the predict() function. It works like this:

predict(svm_linear, tuning_input)

      6       8       9      14      20      22      24      28      32      39 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
     45      52      53      55      66      79      88      97      98     101 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    102     104     106     108     131     135     137     142     145     157 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    163     165     166     177     188     191     195     201     202     203 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    211     214     216     222     243     244     249     257     264     265 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    269     270     290     291     292     293     295     296     307     321 
   spam    spam    spam    spam    spam    spam nonspam    spam nonspam    spam 
    325     330     331     337     341     342     344     349     367     372 
nonspam    spam nonspam    spam    spam    spam    spam    spam    spam    spam 
    374     379     380     395     396     404     407     409     415     423 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    424     425     436     445     447     448     451     452     459     460 
   spam    spam    spam nonspam    spam    spam    spam    spam    spam    spam 
    462     465     467     468     475     479     485     486     489     495 
   spam nonspam nonspam    spam    spam nonspam    spam    spam    spam    spam 
    500     502     506     510     512     518     522     526     527     532 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    534     541     542     561     564     566     567     569     578     579 
   spam    spam    spam    spam    spam    spam nonspam    spam    spam    spam 
    584     586     588     598     615     622     626     630     639     642 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    644     654     660     665     672     675     679     687     692     694 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    699     703     707     714     717     721     725     733     734     748 
   spam    spam    spam    spam    spam    spam    spam    spam    spam nonspam 
    751     757     759     766     770     773     778     780     781     785 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    793     809     810     822     827     831     841     845     851     861 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    868     869     872     873     874     887     888     894     899     900 
   spam    spam    spam    spam    spam    spam    spam nonspam    spam    spam 
    907     912     914     917     922     926     936     942     943     944 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
    945     946     947     955     957     958     959     961     963     965 
   spam nonspam nonspam    spam    spam    spam    spam    spam    spam nonspam 
    968     972     978     979     981     982     984     992     994    1004 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1009    1013    1016    1017    1020    1030    1033    1037    1040    1055 
   spam    spam    spam    spam nonspam    spam    spam    spam    spam    spam 
   1071    1075    1077    1079    1082    1087    1092    1096    1099    1102 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1103    1106    1116    1117    1121    1126    1128    1131    1133    1136 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1139    1149    1150    1160    1170    1174    1186    1192    1193    1194 
   spam    spam    spam    spam    spam    spam nonspam    spam nonspam    spam 
   1201    1203    1204    1207    1216    1222    1224    1233    1236    1239 
   spam    spam    spam nonspam    spam    spam nonspam nonspam nonspam    spam 
   1240    1250    1253    1254    1258    1259    1262    1268    1276    1283 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1286    1290    1292    1293    1297    1299    1310    1314    1318    1320 
   spam    spam    spam nonspam    spam    spam    spam    spam    spam    spam 
   1321    1323    1324    1335    1339    1342    1345    1351    1356    1359 
   spam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1366    1368    1373    1374    1376    1381    1384    1385    1398    1399 
nonspam    spam    spam    spam    spam    spam    spam    spam    spam    spam 
   1400    1404    1409    1425    1431    1434    1435    1444    1450    1455 
   spam nonspam    spam    spam    spam    spam    spam    spam    spam nonspam 
   1456    1457    1458    1459    1468    1474    1475    1476    1478    1479 
   spam nonspam    spam    spam    spam    spam    spam    spam    spam nonspam 
   1484    1487    1489    1491    1492    1499    1513    1517    1518    1524 
   spam    spam nonspam    spam    spam    spam    spam    spam    spam    spam 
   1531    1533    1534    1547    1553    1558    1560    1572    1573    1574 
   spam    spam nonspam    spam    spam    spam    spam nonspam    spam    spam 
   1577    1583    1586    1598    1602    1603    1610    1628    1630    1631 
   spam    spam nonspam    spam    spam    spam    spam    spam    spam    spam 
   1636    1642    1644    1650    1655    1656    1657    1659    1660    1667 
nonspam nonspam    spam nonspam nonspam    spam    spam nonspam    spam    spam 
   1668    1672    1686    1693    1694    1695    1702    1707    1708    1718 
   spam    spam    spam    spam    spam    spam    spam    spam    spam nonspam 
   1720    1722    1724    1732    1745    1752    1759    1768    1770    1775 
   spam nonspam nonspam    spam    spam nonspam    spam    spam    spam nonspam 
   1781    1782    1785    1787    1794    1799    1811    1827    1835    1836 
   spam    spam    spam    spam    spam    spam    spam nonspam nonspam nonspam 
   1844    1848    1855    1859    1864    1866    1872    1878    1880    1883 
   spam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   1887    1896    1902    1915    1922    1953    1960    1962    1973    1974 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   1977    1980    1990    1992    1993    1995    1998    1999    2006    2018 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2023    2024    2028    2030    2037    2039    2041    2046    2053    2059 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2060    2061    2069    2072    2078    2080    2081    2083    2089    2095 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam 
   2099    2110    2114    2116    2118    2120    2131    2136    2137    2144 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2147    2150    2151    2166    2167    2169    2175    2181    2184    2194 
nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam nonspam 
   2200    2201    2205    2208    2212    2225    2240    2241    2245    2247 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2248    2255    2257    2258    2259    2265    2267    2276    2280    2283 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2284    2286    2289    2290    2293    2304    2306    2318    2321    2335 
nonspam nonspam nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam 
   2336    2344    2347    2360    2361    2370    2372    2373    2384    2399 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2408    2413    2414    2419    2421    2428    2437    2439    2444    2445 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2449    2451    2452    2454    2462    2463    2464    2467    2469    2480 
nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam nonspam 
   2481    2490    2494    2524    2527    2532    2537    2541    2555    2572 
   spam nonspam nonspam nonspam nonspam    spam    spam nonspam nonspam nonspam 
   2573    2574    2576    2580    2584    2586    2589    2607    2609    2616 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam 
   2625    2628    2637    2639    2640    2643    2648    2652    2655    2665 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2671    2681    2684    2685    2693    2698    2703    2704    2708    2711 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2716    2738    2751    2753    2761    2763    2765    2768    2770    2777 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2781    2782    2785    2787    2804    2813    2824    2825    2830    2831 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2833    2844    2849    2850    2853    2858    2859    2862    2865    2866 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2873    2875    2878    2881    2887    2893    2894    2903    2906    2907 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam nonspam 
   2908    2909    2910    2913    2920    2933    2935    2940    2947    2951 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   2952    2954    2956    2958    2959    2961    2964    2967    2969    2974 
nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam nonspam nonspam 
   2977    2979    2987    2989    2990    2999    3001    3010    3016    3019 
nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam    spam 
   3021    3023    3028    3039    3040    3042    3052    3053    3061    3069 
nonspam nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam 
   3072    3074    3078    3087    3093    3097    3102    3108    3109    3118 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam nonspam 
   3124    3138    3140    3150    3152    3153    3157    3162    3166    3168 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam nonspam 
   3169    3175    3176    3193    3199    3201    3218    3228    3231    3236 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3237    3245    3254    3259    3260    3263    3265    3269    3271    3276 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam 
   3279    3283    3287    3288    3295    3299    3305    3306    3308    3309 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3313    3315    3316    3323    3325    3328    3330    3332    3338    3355 
   spam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3360    3366    3384    3387    3389    3399    3403    3408    3409    3414 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3415    3418    3426    3430    3431    3434    3442    3452    3457    3462 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam 
   3468    3476    3478    3479    3487    3501    3532    3537    3538    3539 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3541    3544    3546    3554    3562    3568    3573    3582    3585    3594 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3595    3609    3610    3614    3618    3623    3625    3629    3639    3651 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3652    3653    3655    3659    3665    3666    3677    3684    3692    3699 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3706    3711    3718    3719    3732    3739    3747    3754    3756    3757 
nonspam nonspam nonspam nonspam    spam    spam nonspam nonspam nonspam nonspam 
   3758    3762    3764    3776    3779    3794    3803    3809    3821    3822 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3826    3828    3839    3844    3855    3859    3864    3867    3871    3873 
nonspam    spam nonspam nonspam nonspam nonspam nonspam nonspam nonspam    spam 
   3878    3888    3894    3897    3898    3903    3908    3925    3927    3928 
nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam nonspam nonspam 
   3932    3934    3947    3955    3958    3975    3976    3978    3980    3985 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   3991    3992    3993    4002    4004    4006    4011    4014    4027    4032 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4035    4043    4048    4078    4080    4083    4085    4087    4088    4094 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4097    4114    4119    4120    4121    4123    4124    4129    4138    4143 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4148    4152    4154    4160    4167    4169    4178    4190    4194    4195 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4203    4213    4215    4217    4223    4232    4234    4239    4254    4260 
nonspam nonspam    spam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4268    4273    4281    4296    4303    4306    4312    4315    4317    4318 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4333    4337    4338    4339    4344    4346    4349    4352    4361    4362 
nonspam    spam nonspam nonspam nonspam nonspam nonspam nonspam    spam nonspam 
   4367    4369    4377    4379    4380    4387    4399    4403    4406    4408 
nonspam nonspam nonspam nonspam nonspam    spam nonspam nonspam nonspam nonspam 
   4410    4411    4418    4428    4432    4435    4447    4456    4458    4460 
nonspam nonspam    spam    spam nonspam nonspam nonspam nonspam nonspam    spam 
   4463    4470    4472    4473    4474    4481    4485    4512    4518    4535 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
   4541    4564    4573    4579    4583    4586    4587    4588    4591    4601 
nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam nonspam 
Levels: nonspam spam

You should get spammed with some “spam” and “nonspam”! Not very helpful, but it lets us see that the SVM is working.

Let’s use the tibble() function to bundle it all into one big data frame table:

tuning_results <- tibble(tuning_truth,
  linear = predict(svm_linear, tuning_input),
  poly = predict(svm_poly, tuning_input),
  radial = predict(svm_radial, tuning_input),
  sigmoid = predict(svm_sigmoid, tuning_input)
)

We want to check how many instances we have of where the tuning_truth matches with each of the other four columns: each one is where we correctly identified a message.

The way that we built the tuning_results table is a little annoying, because we really want to do these comparisons systematically.

So, let’s pivot the data longer by reworking the columns:

tuning_results1 <- tuning_results |> pivot_longer(cols = !tuning_truth)

After this, we check for matches. There are four kinds of these!

tuning_results2 <- tuning_results1 |>
  mutate(
    tp = (tuning_truth == "spam" & value == "spam"), # True positives (SVM got it right!)
    tn = (tuning_truth == "nonspam" & value == "nonspam"), # True negatives (SVM got it right!)
    fp = (tuning_truth == "nonspam" & value == "spam"), # False positive (SVM made a mistake)
    fn = (tuning_truth == "spam" & value == "nonspam")
  ) # False negative (SVM made a mistake)

Count up the occurrences of each of these

tuning_results3 <- tuning_results2 |>
  group_by(name) |> # Group by the kernel names
  summarize(
    tp = sum(tp),
    tn = sum(tn),
    fp = sum(fp),
    fn = sum(fn)
  )

7.5.1 2x2 Confusion Matrices

A 2x2 confusion matrix shows the performance of a model on a sample of size \(n\) by organizing the \(n\) predictions into each of the four possible outcomes and showing the counts for each outcome.

A confusion matrix allows one to see how much or how little a model “confuses” the two classifications.

**Sample Confusion Matrix**
Actual \ Predicted	Positive (PP)	Negative (PN)
Positive (P)	True Positive (TP) count	False Negative (FN) count
Negative (N)	False Positive (FP) count	True Negative (TN) count

7.6 Testing stage

With the counts of true/false positives/negatives, there are many possible kinds of scores you can make to determine which SVM kernel works best.

If you divide the counts by the the number of predictions \(n\) the size of your testing data, you get corresponding “rates”.

Different disciplines tend to prefer some of these scores over others: medical tests often report sensitivity and specificity, while most deep learning researchers prefer F1 scores.

If you’re curious, have a look at

https://en.wikipedia.org/wiki/Sensitivity_and_specificity

Just using the formulas on that page, we can compute a few of these:

tuning_results3 |>
  mutate(
    accuracy = (tp + tn) / (tp + tn + fp + fn),
    sens = tp / (tp + fn),
    spec = tn / (tn + fp),
    ppv = tp / (tp + fp),
    npv = fn / (tn + fn),
    f1 = 2 * tp / (2 * tp + fp + fn)
  )

# A tibble: 4 × 11
  name       tp    tn    fp    fn accuracy  sens  spec   ppv    npv    f1
  <chr>   <int> <int> <int> <int>    <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>
1 linear    346   502    31    41    0.922 0.894 0.942 0.918 0.0755 0.906
2 poly      184   520    13   203    0.765 0.475 0.976 0.934 0.281  0.630
3 radial    346   511    22    41    0.932 0.894 0.959 0.940 0.0743 0.917
4 sigmoid   335   484    49    52    0.890 0.866 0.908 0.872 0.0970 0.869

I noticed that ‘linear’ was the best in my case at least in terms of the accuracy and the F1 score, but it’s awfully close to the ‘radial’ score. This is now a situation where plotting can help, if you like.

Finally, you can repeat with just the svm_linear on the test data!

7.6.1 Another Example

The graphics in Figure 7.1 are from an SVM trained on data about home sales.

We want to classify Home QUALITY a factor with three different levels: LOW, MEDIUM, and HIGH.

Our predictors are SALES PRICE and YEAR_BUILT.
Figure 7.1 (a) show the points overlap so we cannot draw a simple line separating the points.
Figure 7.1 (b) shows the linear kernel.
Figure 7.1 (c) shows the radial kernel.

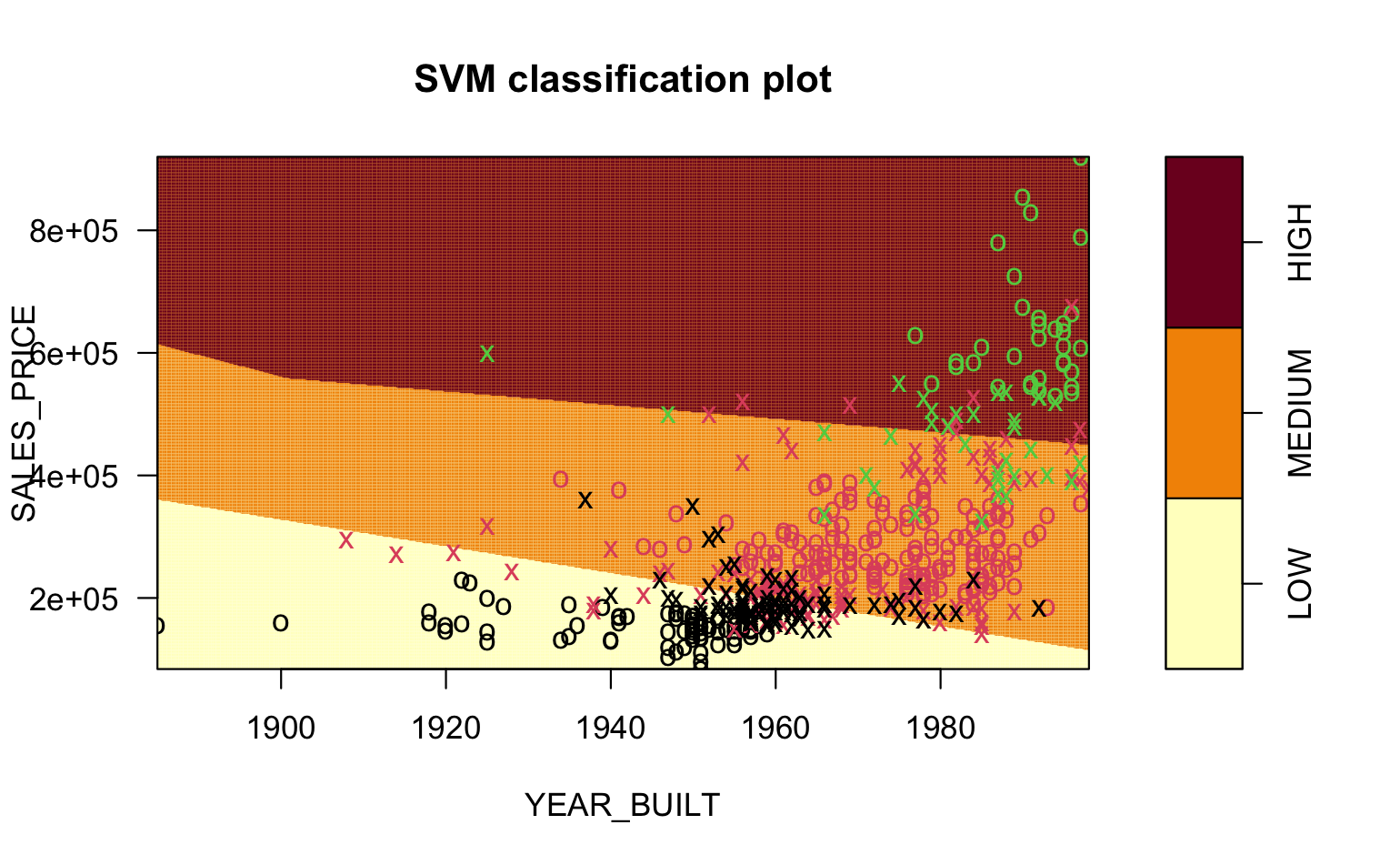
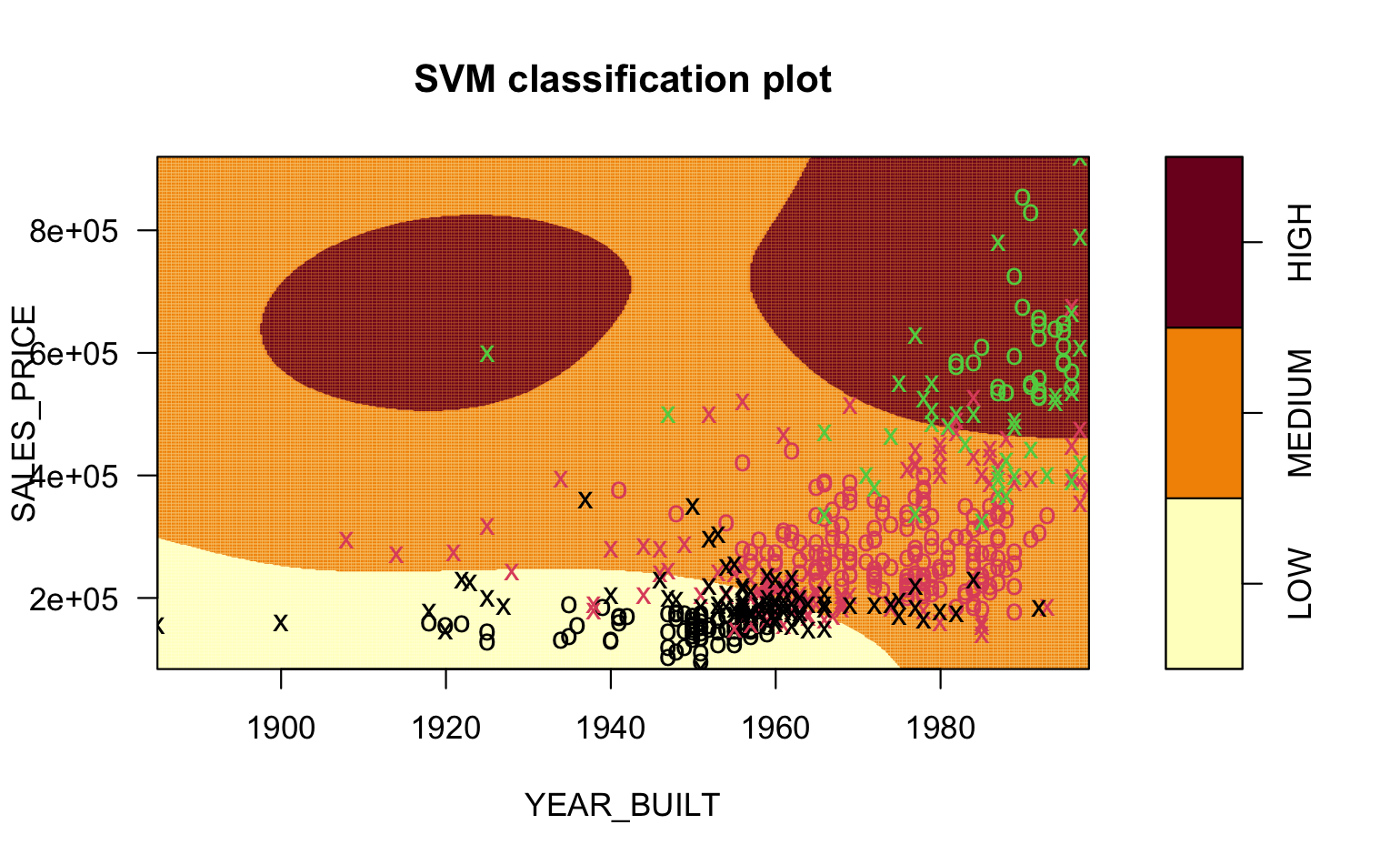
You can see the vastly different shapes of the boundaries for the different regions in the pictures.

You can see the points that are Errors in prediction, e.g., green circles in the MEDIUM region, red circles in either HIGH or LOW, and black circles in the MEDIUM region.
Visually, it looks like the Radial kernel might be a better solution.

It can be challenging to visualize what is happening with the different kernels.

In short, a kernel transforms the data into a higher dimensional space, then fits the best multi-dimensional hyperplane it can, and then projects the result back into the original multi-dimensional space.
This YouTube video provides a nice example for a polynomial kernel.

7.7 Summary

Classifiers are an important set of methods for working with categorical response variables.

We have examined just a few forms of classifiers as there are many and there are also many packages with different implementations of the methods.

As with Regression methods, there is no “best classifier” as their performance depends on the underlying (hidden) multi-dimensional structure of the data and how well different methods might fit the data without overfitting.

SVM is a popular method as it supports multiple kernels and is computationally efficient.

7.8 Exercise

Locate a dataset that has a number of numerical variables that you can use as explanatory variables and a binary (boolean) variable that you can use as a response variable. You could use the dataset from the previous lessons if you like.

Caution: some datasets do not separate well according to the response variables. It’s better if the data separate, but don’t worry if you can’t find a good dataset. The process will “work”, but it might not work well. Be sure to explain your findings; that’s more important than getting good results!

Split your chosen dataset into the three training/tuning/test samples. Save each off each as a CSV file and upload these.
Train at least three SVMs on your training data, being careful to explain which variables are the response and the explanatory variables. Feel free to experiment with different hyperparameters beyond what was done in the worksheet above. The hyperparameters you need might be quite different!
Using your tuning set, select which SVM performs the best… and then…
… determine its performance using the testing set.
Make sure to explain Steps 4 and 5 in comments in your Quarto file!