4 Multivariate Data Analysis
Multivariate Statistics, Scatter Plots, Facetting Plots
4.1 Introduction
This module focuses on the analysis of two or more variables at once - bi-variate or multi-variate data.
Learning Outcomes
- Create bivariate point plots and box plots
- Use plot aesthetics to code by additional variables
Add and interpret linear and non-linear smoothers
4.1.1 References
- Elegant Graphics for Data Analysis {ggplot2} package (Wickham 2016)
- {palmerpenguns} data package (Horst, Hill, and Gorman 2020)
4.2 Multivariate Data
Let’s continue with the two datasets from the previous lesson.
4.3 Numerical vs. Numerical Data (Scatterplots)
Here’s the base R version… Plot a scatterplot and line of best fit. Also, find the p-value that tells how meaningful this model is.
plot(house_ed_gdp_joined$has_internet,
house_ed_gdp_joined$has_computer) # X then Y.
myline <- lm(house_ed_gdp_joined$has_computer ~
house_ed_gdp_joined$has_internet) # Y then X .
abline(myline) # Hopefully that worked!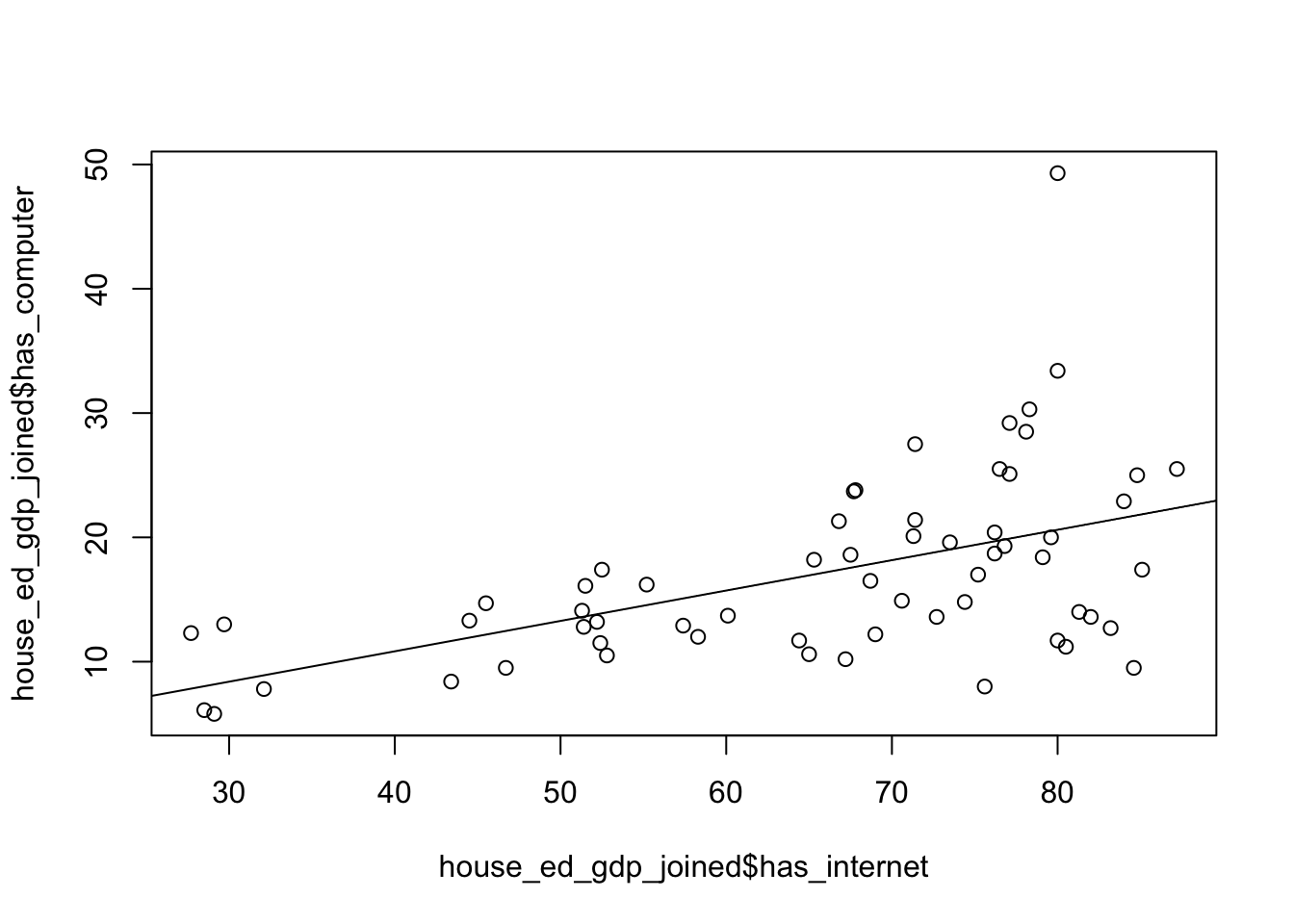
If you must stack many layers together, you may need the command part(new=T) to prevent the graphic from clearing. Note how tidyverse does this very differently!
Call:
lm(formula = house_ed_gdp_joined$has_computer ~ house_ed_gdp_joined$has_internet)
Residuals:
Min 1Q Median 3Q Max
-12.2499 -3.4249 -0.6234 3.1140 28.6754
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.05276 3.57662 0.294 0.77
house_ed_gdp_joined$has_internet 0.24465 0.05282 4.632 2.04e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.547 on 59 degrees of freedom
Multiple R-squared: 0.2667, Adjusted R-squared: 0.2542
F-statistic: 21.45 on 1 and 59 DF, p-value: 2.044e-05 (Intercept) house_ed_gdp_joined$has_internet
1.0527597 0.2446474 In the summary, you get all the necessary information about your linear model, including the p-value. In this class, if our p-value is smaller than 0.05, we will say it is significant. This means it is statistically significant at the 95% level.
In tidyverse, we can make scatter plots with Loess curves! There are many ways to call the same functions inside tidyverse. Try each of these commands and verify that they are the same.
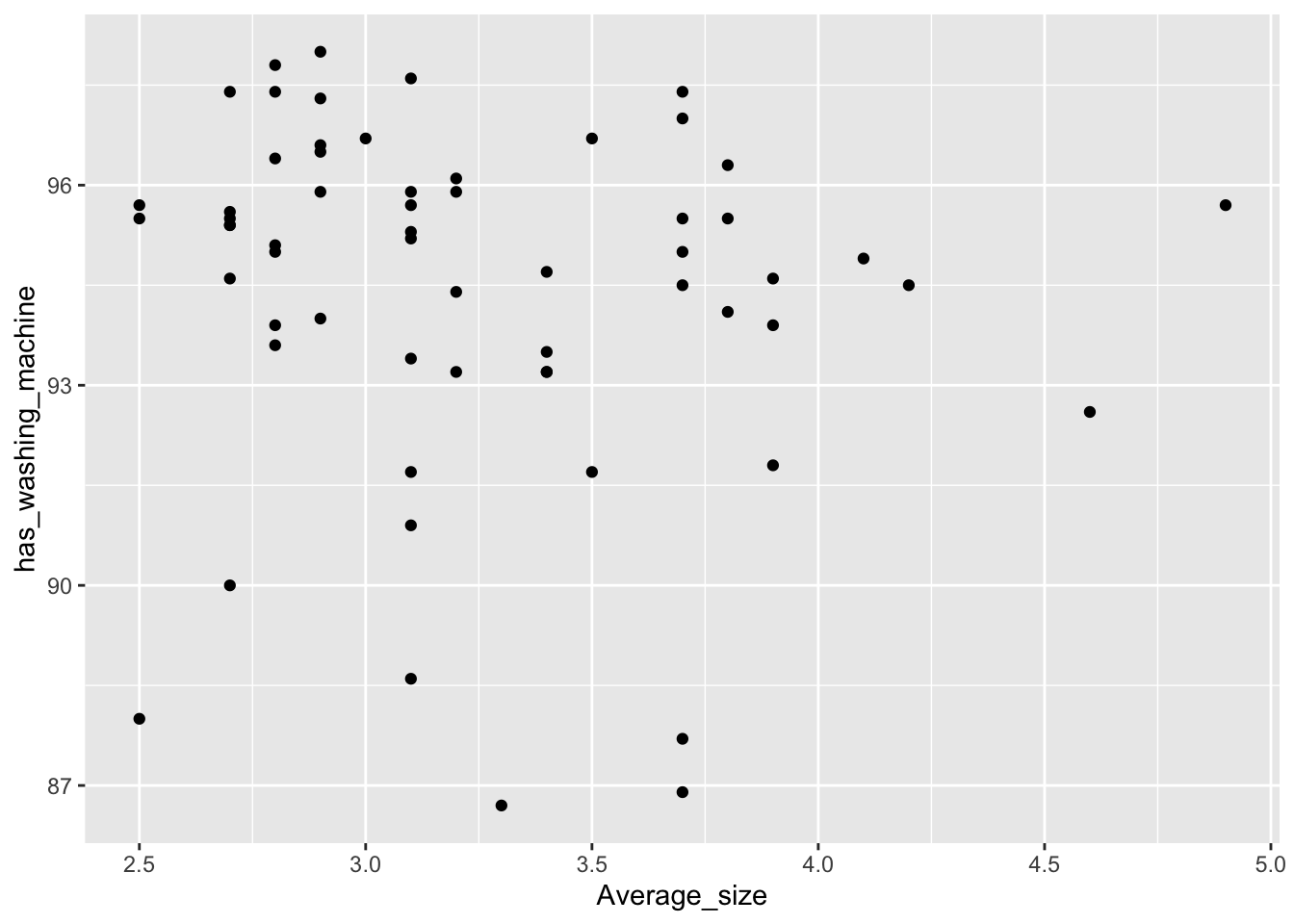
Arguments inside the ggplot command will apply to all the layers in the same plot. If you prefer to use different choices for different layers, give those arguments only in the layers. Each + (whatever) is a new layer.
The |> is called a Magrittr “pipe”. It has a few more features than the R Native Pipe |>. It is also frequently the punchline for jokes about R. Many programming environments have a pipe, but only R’s pipe looks like that! You should think of a pipe as a physical pipeline that takes things from one place and transports them elsewhere.
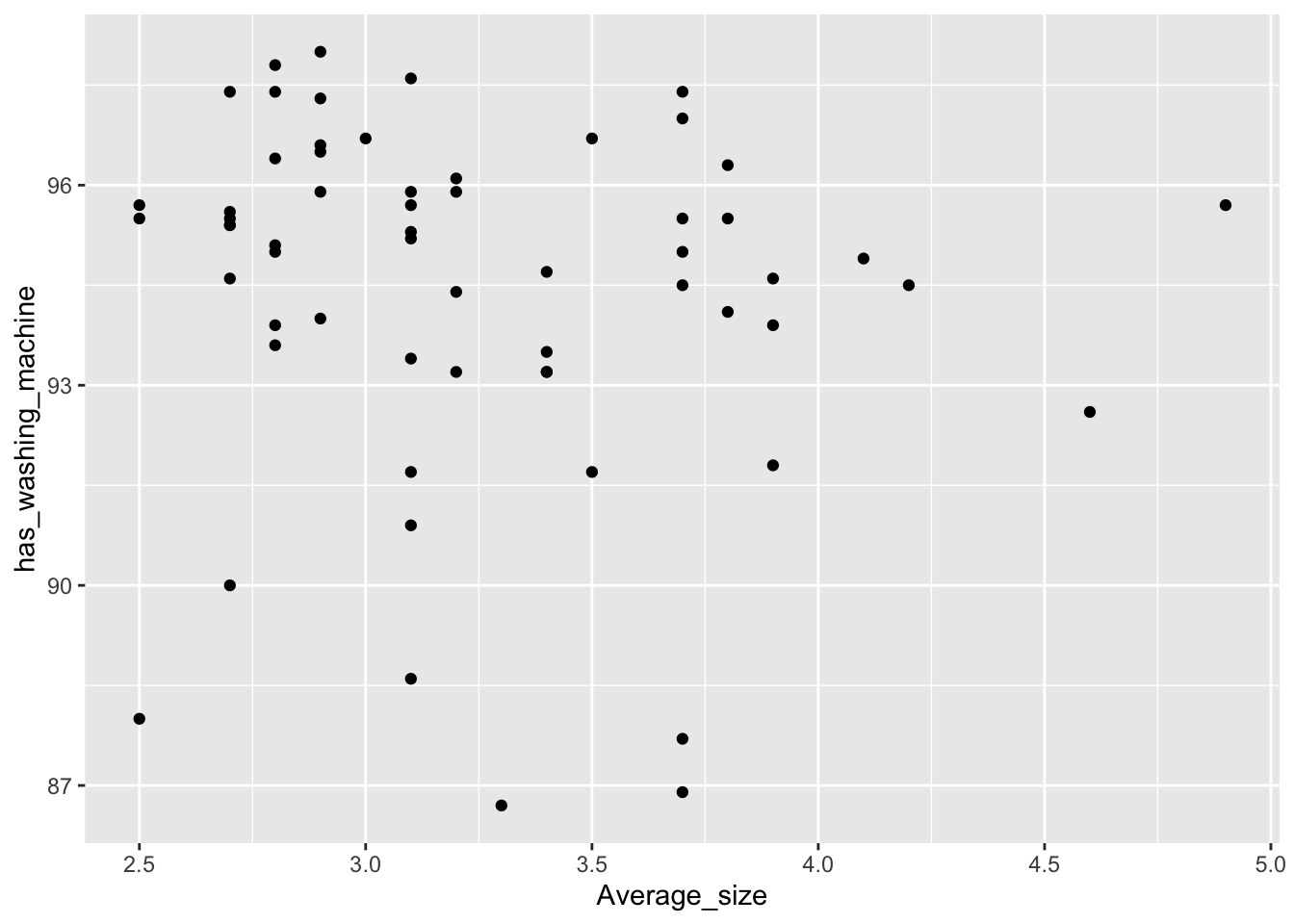
What if we want a scatterplot (numerical vs. numerical) but we wish to color the points be a categorical variable?
house_ed_gdp_joined |>
ggplot(aes(x = Average_size, y = has_washing_machine, color = Municipality)) +
geom_point()
Instead of color, you could choose to change the shape or saturation. Many options are available for the designation of categorical variables. Notice the x= and y=. When you use those, you can change the default order for the input variables.)
When you add an argument like color or shape in an aes(), the default is to add a legend as we see above. With 61 points, that shrinks the plot quite a bit.
There are a number of “tricks” , arguments, by which you can adjust the plot if you really want to see the points and the legend.
- You may need to install a new package to use the
geom_label_repel(). In the Console, typeinstall.packages("ggrepel")and say yes if it asks if you want to continue.
house_ed_gdp_joined |>
ggplot(aes(x = Average_size, y = has_washing_machine,
color = Municipality, label = Municipality)) +
geom_point() +
guides(color = guide_legend(ncol = 9)) + # Set number of columns in legend
theme(legend.position = "bottom",
legend.text = element_text(size = 8), # Shrink legend labels
legend.title = element_text(size = 9), # Shrink legend title)
legend.box = "horizontal", # Ensures horizontal stacking
legend.spacing.x = unit(0.5, "cm")
) +
ggrepel::geom_label_repel(size = 2.5, label.size = 0, max.overlaps = 14)
Instead of color, you could choose to change the shape or saturation. Many options are available for the designation of categorical variables. Notice the x= and y=. When you use those, you can change the default order for the input variables.)
A scatter plot can also be colored based on a numerical variable.
house_ed_gdp_joined |>
ggplot(aes(x = Average_size, y = has_washing_machine, color = has_car)) +
geom_point()
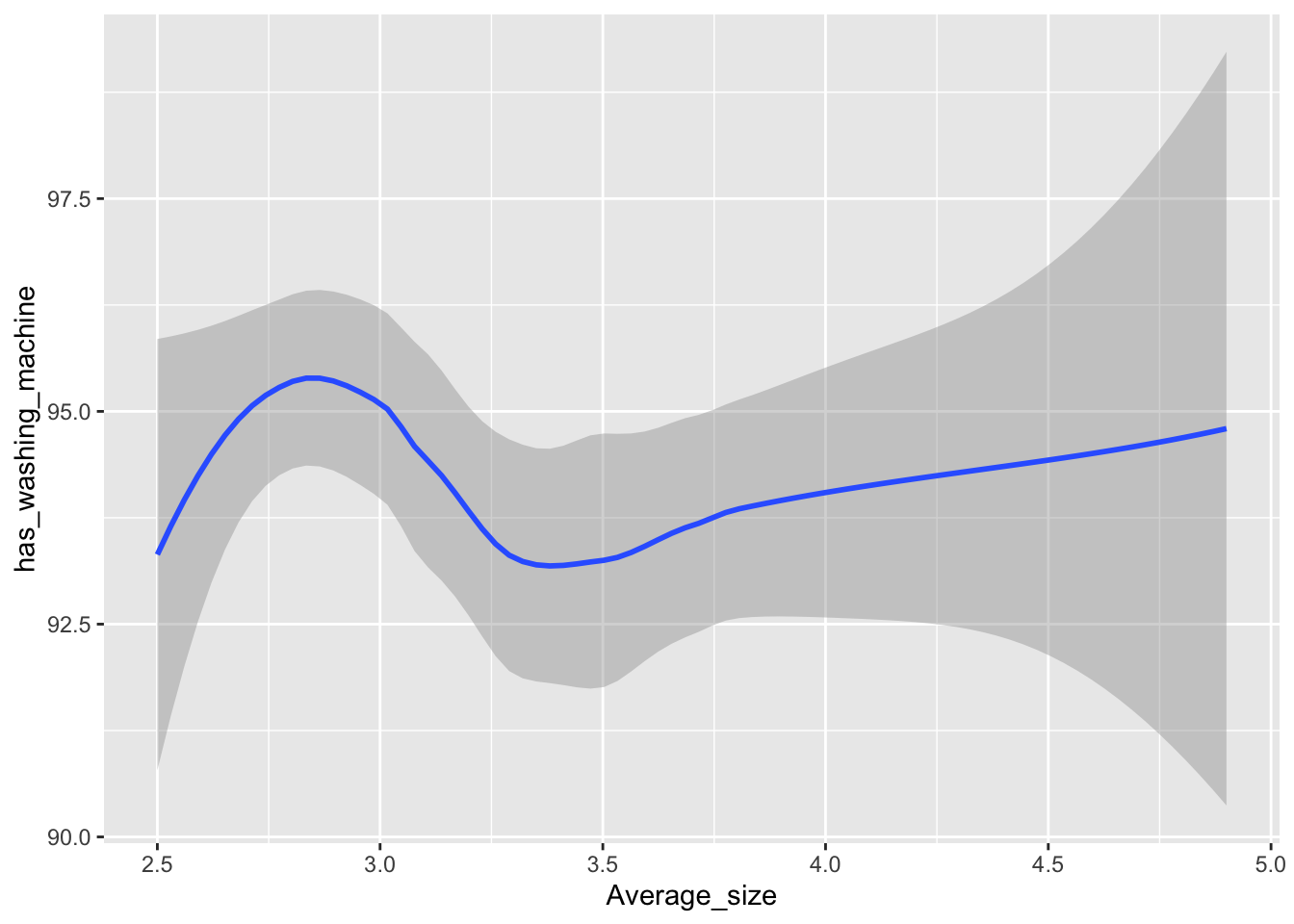
These two plots are grammatically very similar, but one gives a scatter plot while the other gives a Loess curve.
4.4 Working with layers (comparing numerical and categorical data)
We can put two layers together like this:
house_ed_gdp_joined |>
ggplot() +
geom_point(mapping = aes(x = Average_size, y = has_washing_machine,
color = Municipality)) +
geom_smooth(mapping = aes(x = Average_size, y = has_washing_machine))
Notice how we moved the aes() out of ggplot and split it onto the two layers we wanted. This opens up lots of graphical possibilities!
Let’s look at how big families are:
You can also do this using tidyverse, which is perhaps a bit less error-prone:
Once again, which style you prefer is a matter of preference. But regardless, we can now use this newly recoded variable.
Another option is to use different linetypes for different categorical values.
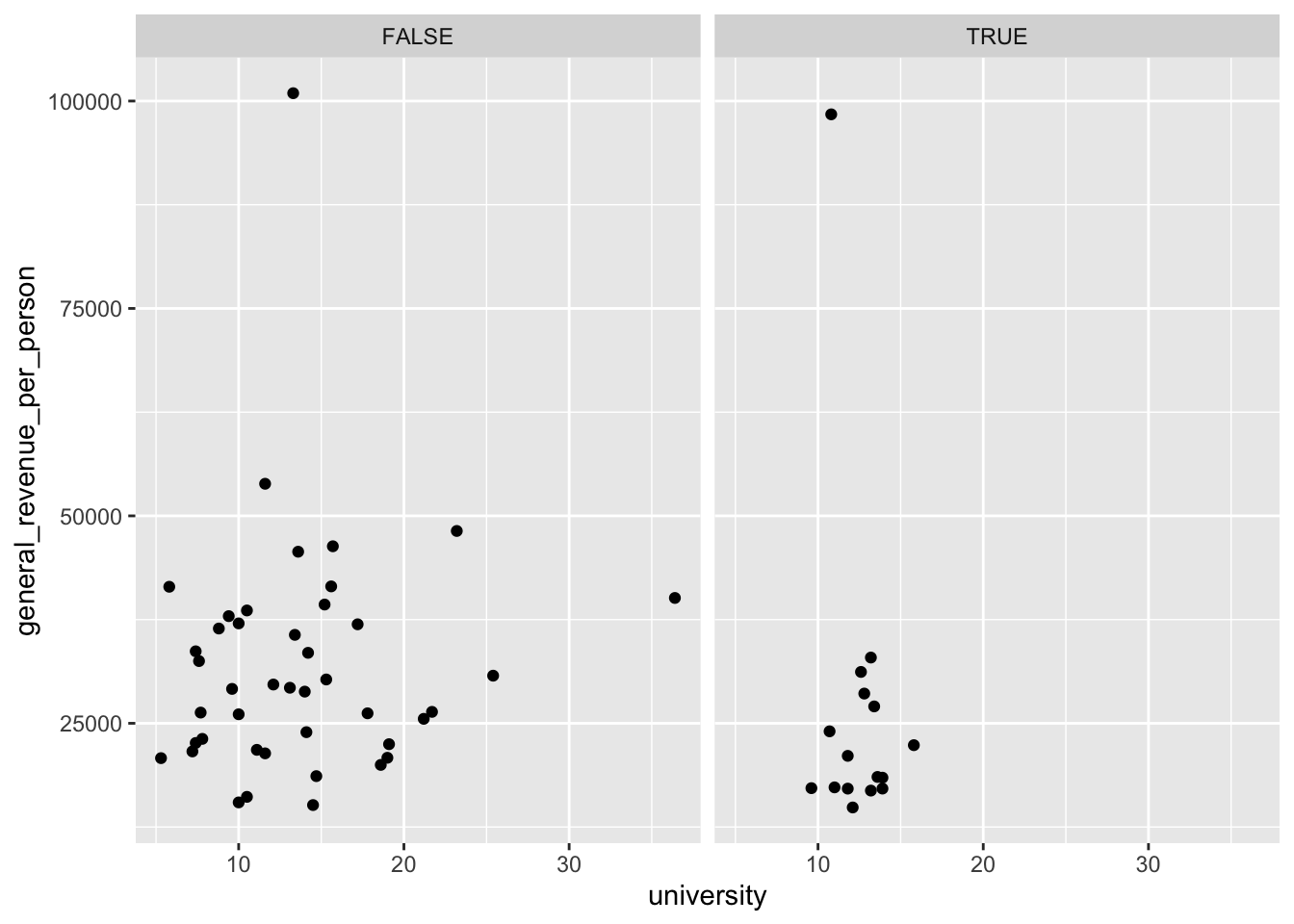
mywk |>
ggplot(aes(x = university, y = general_revenue_per_person,
linetype = largeFam)) +
geom_smooth()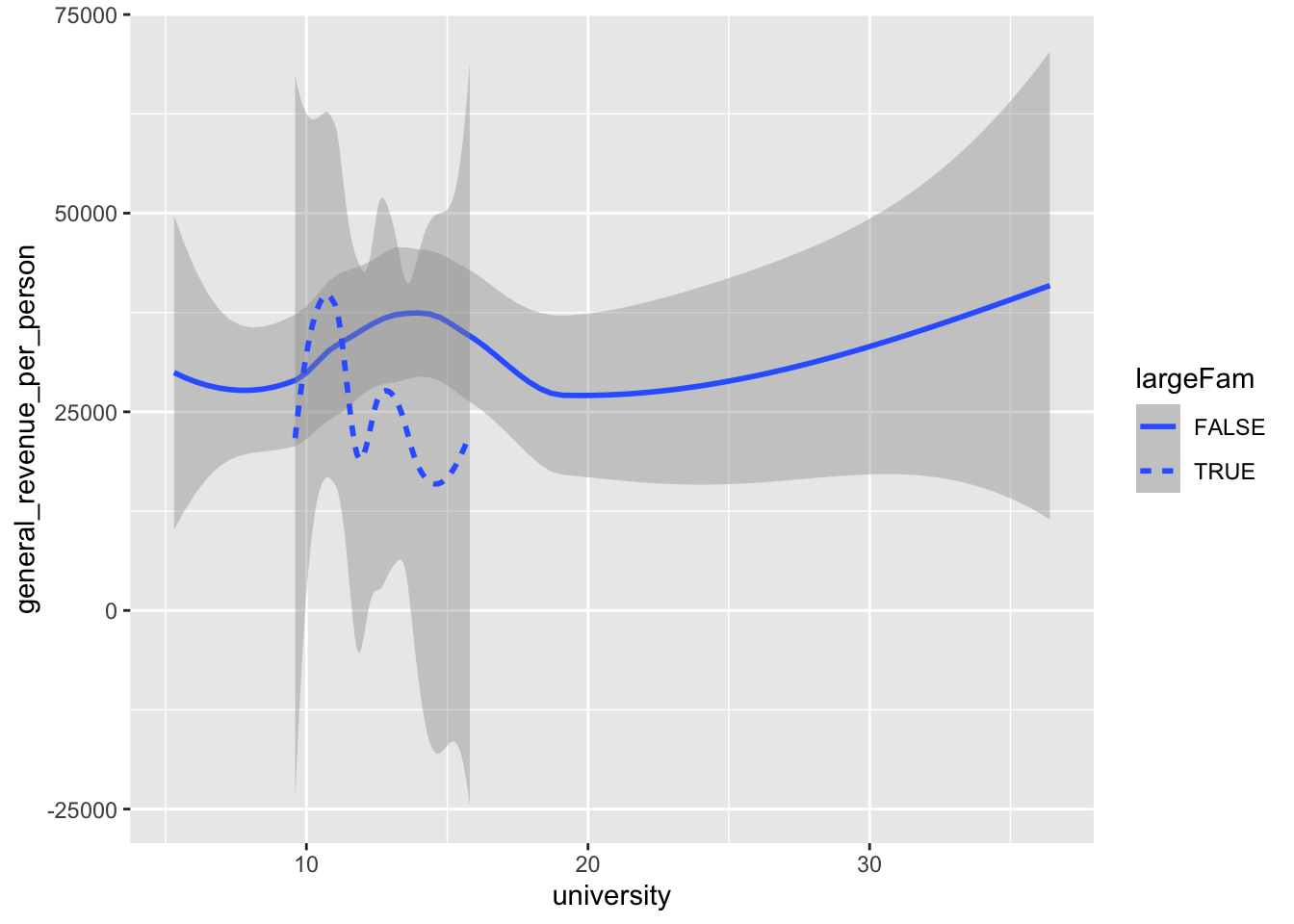
mywk |>
ggplot(aes(x = university, y = general_revenue_per_person,
linetype = largeFam)) +
geom_smooth(se = FALSE)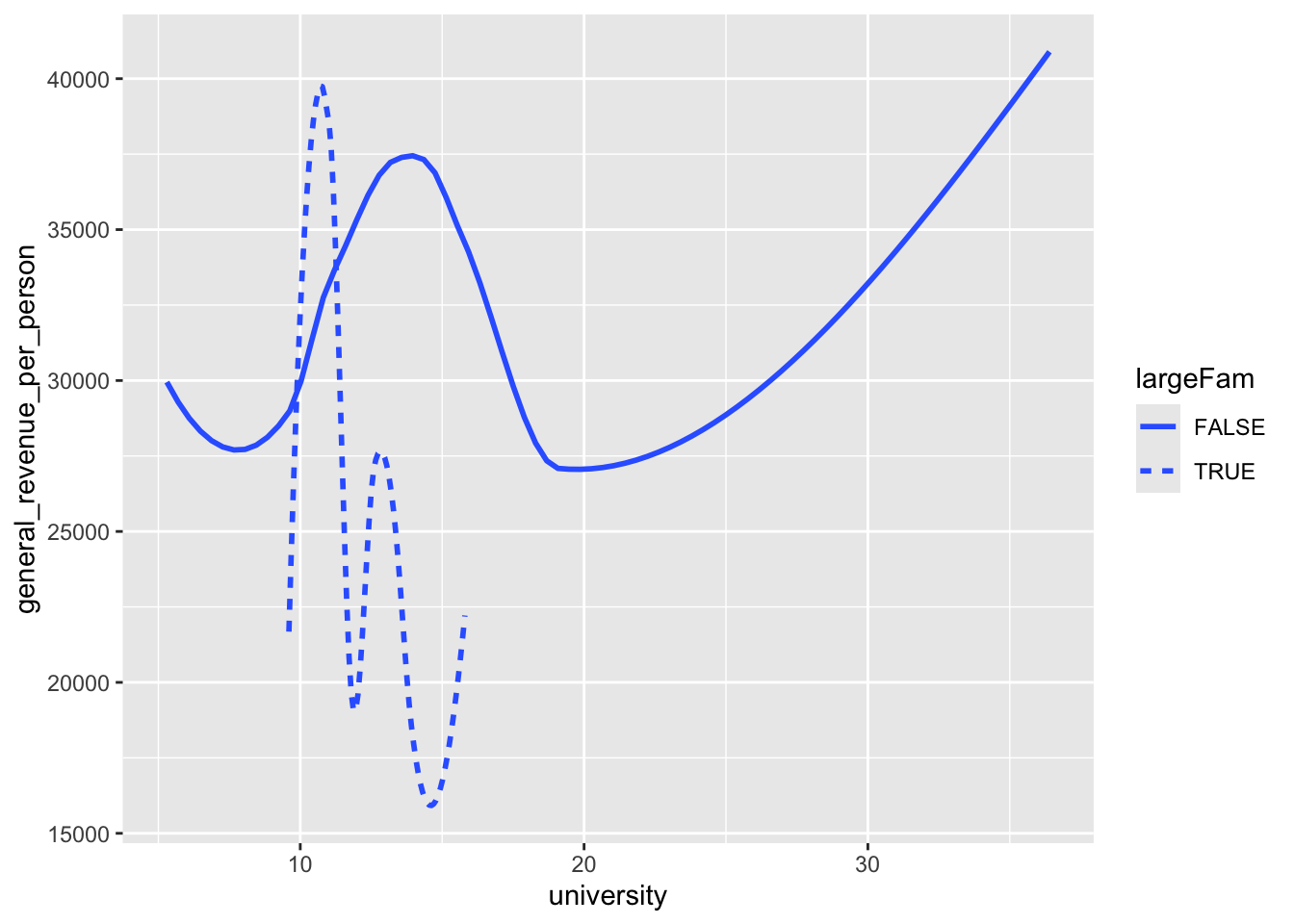
The option se = FALSE gets rid of the “standard error” neighborhood around the curve.
The order of the layers does in fact matter!
mywk |>
ggplot(aes(university, general_revenue_per_person)) +
geom_point(aes(color = largeFam)) +
geom_smooth()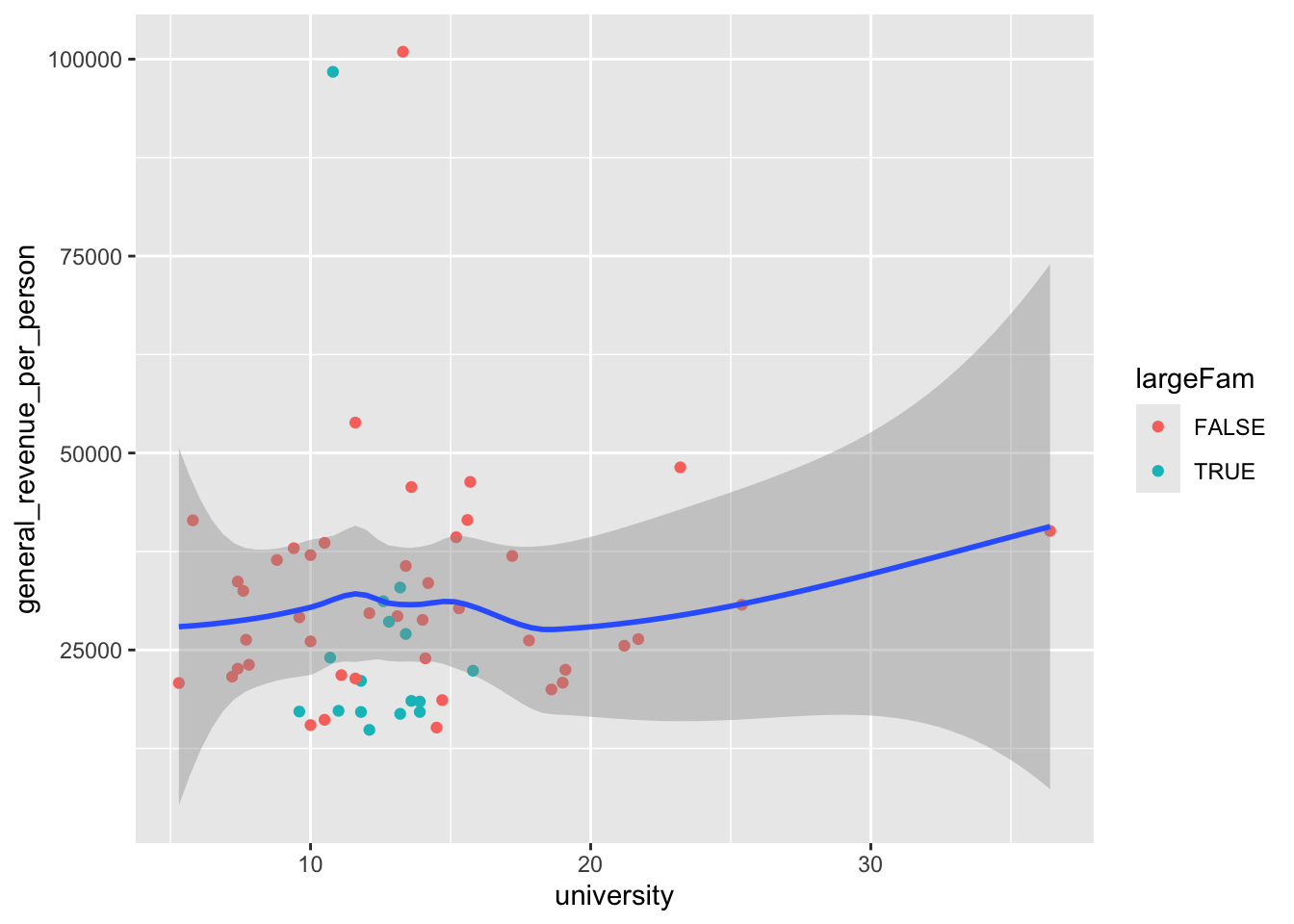
Invert the last two layers to see what happens!
4.5 Facet plots
Rather than just coloring the categories, you could also make several side-by-side plots for each category. In tidyverse, these are called facets. There are options to control how many of these plots will go in a row or column if you need that.
4.6 Adding “Scaffolding”
We have done a number of plots for exploratory data analysis where we focused on the content of the plot.
When we want to communicate our findings, we often want to publish or show one or plots to others. To help them interpret the plots, we often want to add additional elements besides the data.
Edward Tufte’s book The Visual Display of Quantitative Information, remains influential in graphic design. Alberto Cairo has published several books in the past few years about visualization design as well.
Tufte refers to elements like axis labels, titles, tick marks, and grid lines as scaffolding — they are necessary for interpreting the data but are not the data themselves. These elements should be used sparingly and effectively to avoid clutter and highlight the data.
Tufte distinguishes between:
- Data ink: The ink (or pixels) that represent the core data.
- Non-data ink (scaffolding): Supportive elements like axis lines, tick marks, labels, legends, etc.
Tufte advocates for reducing non-data ink to avoid what he calls the “chartjunk” — visual clutter that detracts from the data.
We want to make it easy for viewers of a graphic to see our interpretation. Unnecessary “chartjunk” increases the “noise in the chart” so it reduces the “signal to noise” ratio which is bad. As Data Scientists we are always seeking to find the “signal” in the midst of “noisy” data.
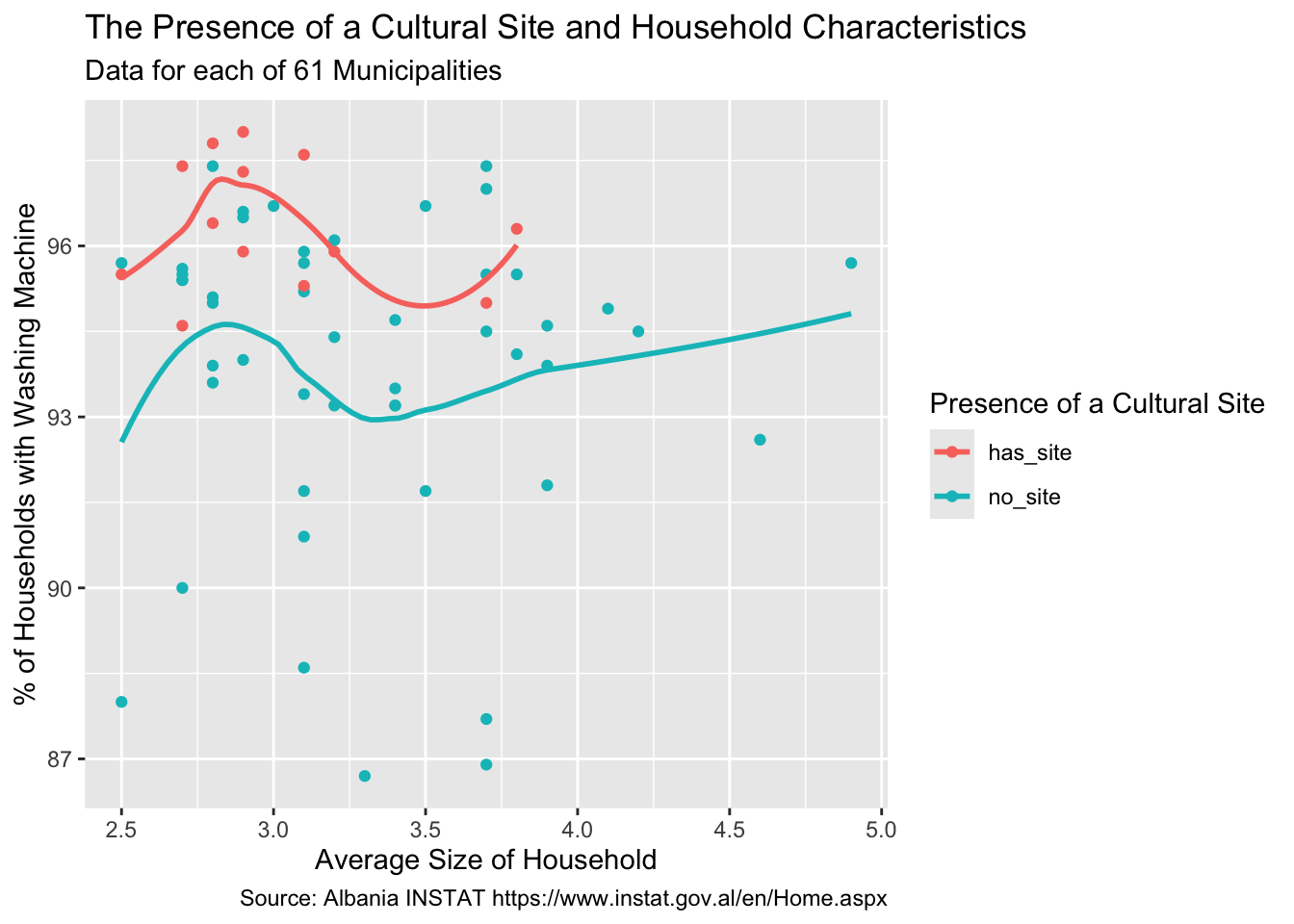
Here is an example of adding labels and titles to a plot to improve its interpretation by others.
- To get the dynamic value of
Municipalities, install the {glue} package by using the console to enterinstall.packages("glue"). - Now you can use code to determine value.
library(glue)
n_obs <- nrow(mywk)
mywk |>
ggplot(aes(Average_size, has_washing_machine, color = culture_site)) +
geom_point() +
geom_smooth(method = loess, se = FALSE) +
labs(
title = "The Presence of a Cultural Site and Household Characteristics",
subtitle = glue("Data for each of {n_obs} Municipalities"),
caption = "Source: Albania INSTAT https://www.instat.gov.al/en/Home.aspx",
x = "Average Size of Household",
y = "% of Households with Washing Machine",
color = "Presence of a Cultural Site" # This sets the legend title
)
4.7 Common ggplot2 Geoms by Plot Type and Variable Types
We have looked at just a few of the plots in the {ggplot2} package. Here is a more complete list. There are packages that build on or extend {ggplot2} as well with even more kinds of plots. If you search for a kind of plot you want to do, you can usually find a way.
| Plot Type | Variable Types | Common geom_*() Functions |
Description |
|---|---|---|---|
| Univariate | Numeric | geom_histogram() |
Histogram of a numeric variable |
geom_density() |
Smoothed density estimate | ||
geom_boxplot() |
Boxplot of a single numeric distribution | ||
geom_violin() |
Violin plot for distribution shape | ||
geom_dotplot() |
Dot plot showing individual data points | ||
| Univariate | Factor | geom_bar() |
Bar chart of counts by category |
geom_col() |
Bar chart with specified heights (e.g., summary stats) | ||
| Bivariate | Numeric vs Numeric | geom_point() |
Scatterplot |
geom_smooth() |
Regression or smooth line | ||
geom_line() |
Line plot, often for time series | ||
geom_hex() / geom_bin2d() |
Binned heatmap for dense numeric data | ||
| Bivariate | Numeric vs Factor | geom_boxplot() |
Boxplot of numeric values by group |
geom_violin() |
Violin plot of numeric distribution by group | ||
geom_jitter() |
Scatter with added noise to avoid overplotting | ||
geom_col() |
Bar plot with numeric summaries by category | ||
| Bivariate | Factor vs Factor | geom_tile() |
Heatmap-style plot showing combinations |
geom_count() |
Circle plot sized by frequency of combinations |
4.8 Summary
Data Visualization, creating graphics or plots, is a core skill in data science to both explore the data, find the signal, as well as communicate the results to others.
The tidyverse in R (and Seaborn/matplotlib in python) provide many tools for creating interesting and beautiful plots. Enjoy!
4.9 Exercise
Use the same dataset as in the previous lesson!
- For two numerical variables, plot a scatterplot and line of best fit.
For this same line, print out the summary results. Type into a comment to report whether this linear model is statistically significant at the 95% confidence level. Type out the formula that is the equation of your line of best fit. (Note: use coef to give you the slope and intercept, but look at the graphic to figure out which is which.)
Using tidyverse, plot a scatterplot colored by a categorical variable.
Plot a scatterplot colored by a numerical variable.
(If your data set contains only two numerical variables, you may have to re-use one of the variables used already. This is fine, even though it’s a bit pointless.)
- Layer two plots on top of each other
Suggest using the + twice in the same plot. This could be a scatterplot with a curve on top, but it doesn’t have to be.
- Make some hypotheses
Since the next lesson will discuss statistical tests, pose some hypotheses about relationships between the variables you’ve observed. Write these down in your Quarto notebook, both so that you don’t forget and to help you work things out.