5  Statistical Tests

Keywords

t-tests, Chi-squared test, Analysis of Variance, ANOVA, Linear Regression

5.1 Introduction

This module focuses on the use of statistical tests in analyzing data.

Learning Outcomes

• Explain the purpose for statistical tests and a Null hypothesis
• Use and interpret the t.test, aov/anova, and lm functions in R
• Generate residual plots in R.

5.1.1 References

• The R Stats Package. See help("stats").

5.2 Statistical Tests

Let’s explore the penguins dataset from the previous lessons.

library(tidyverse)
library(palmerpenguins)
data("penguins")

5.3 Subsets and recoding

You can make several sets of data, split on a categorical variable, or recode variables, or create new variables. We already saw an example of this before

mypenguins <- penguins |>
  mutate(big_penguin = (body_mass_g > 5000))

As we saw then, recoding can be done in base R or tidyverse, so it’s good to get a sense for how to do the task in both dialects. Let’s use base R this time. Note the “stray” commas below! We are filtering rows, taking ALL columns!

large <- mypenguins[mypenguins$big_penguin == "TRUE", ] # Comma warning!!!
small <- mypenguins[mypenguins$big_penguin == "FALSE", ] # Here too!!!

The tidyverse subsetting is a little different. Maybe you’ll like it more… (no tricky commas!)

large <- mypenguins |> filter(big_penguin == "TRUE")
small <- mypenguins |> filter(big_penguin == "FALSE")

Although I usually prefer tidyverse, it’s hard to do a clean recoding using tidyverse. Fortunately, whichever way you prefer to filter, it will work.

Now that we have large and small penguins split this way, a t-test is easy!

t.test(large$flipper_length_mm, small$flipper_length_mm)

    Welch Two Sample t-test

data:  large$flipper_length_mm and small$flipper_length_mm
t = 23.851, df = 160.86, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 22.49402 26.55528
sample estimates:
mean of x mean of y 
 221.0656  196.5409 

If we get a \(p\)-value smaller than 0.05, we can conclude we have found a statistically significant difference between the two groups, at a 95% confidence level!

5.4 Chi-squared Test (Categorical vs. Categorical)

This last graphic we just created begs the question of whether the differences we are seeing in the proportions in the bars is just statistical noise.

Fortunately, we have a test for just this purpose! It’s the chi-square test, and this is how we run it.

newtable <- table(mypenguins$big_penguin, mypenguins$species)
newtable # Shows you what table just did, if you wish to see it.

       
        Adelie Chinstrap Gentoo
  FALSE    151        68     62
  TRUE       0         0     61

chsq <- chisq.test(newtable) # chsq is just a variable to hold your results.
chsq # This gives us a p-value!

    Pearson's Chi-squared test

data:  newtable
X-squared = 132.19, df = 2, p-value < 2.2e-16

chsq$observed

       
        Adelie Chinstrap Gentoo
  FALSE    151        68     62
  TRUE       0         0     61

chsq$expected

       
           Adelie Chinstrap   Gentoo
  FALSE 124.06725  55.87135 101.0614
  TRUE   26.93275  12.12865  21.9386

round(chsq$expected, 2)

       
        Adelie Chinstrap Gentoo
  FALSE 124.07     55.87 101.06
  TRUE   26.93     12.13  21.94

If you look at the output from the chisq.test() function, you will see a \(p\)-value. If that \(p\)-value is less than 0.05, we can conclude the differences we see in the ratios in the plot above are statistically significant. Otherwise, we can guess that the differences we are seeing are likely just due to sampling issues and are probably not relevant.

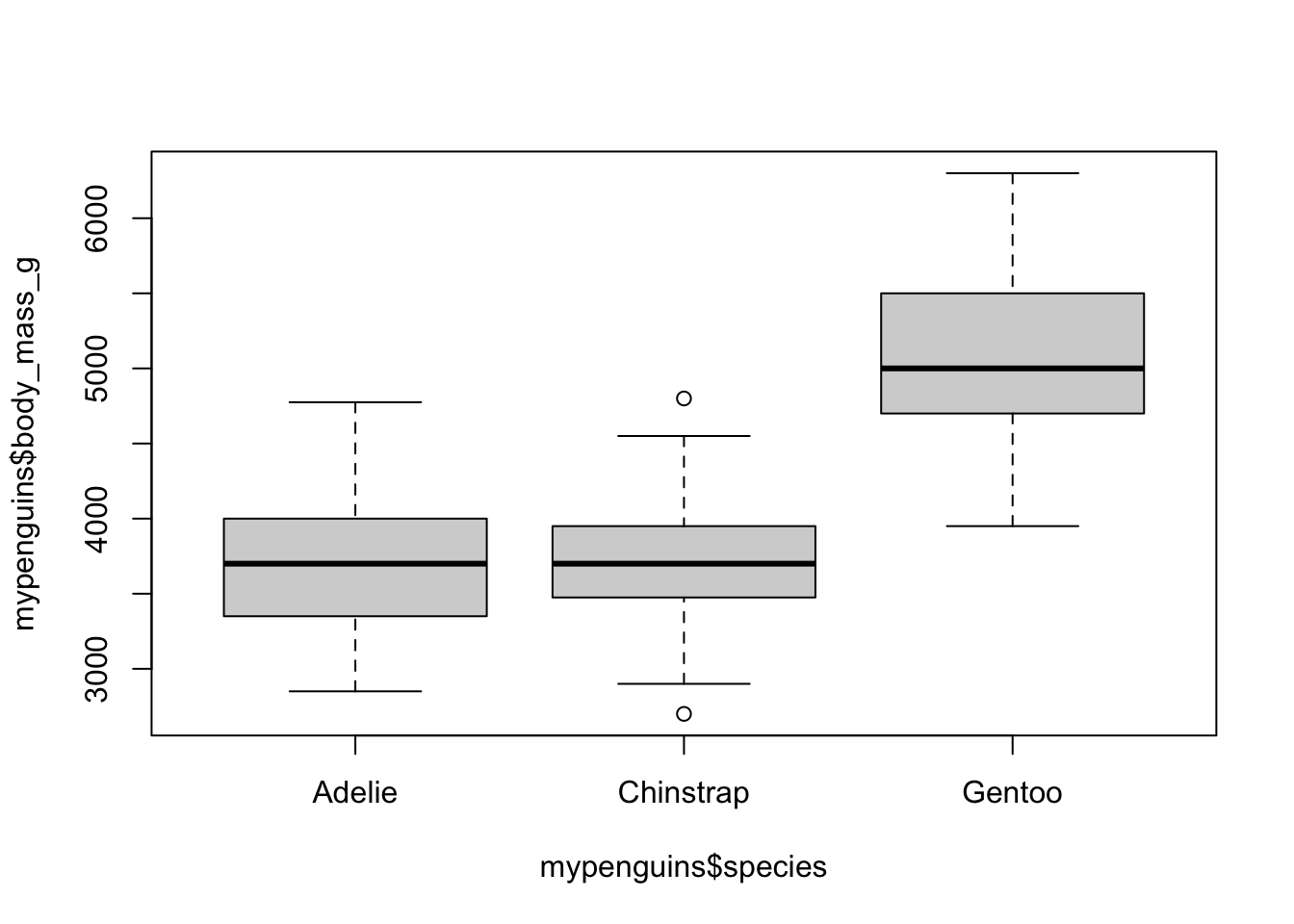
5.5 Box and whisker plots, and ANOVA (Numerical vs. Categorical)

Without using tidyverse, we can get basic boxplots as shown here:

boxplot(mypenguins$body_mass_g ~ mypenguins$species) 

body_mass_g is the numerical variable. species is categorical.

Within tidyverse, as before, we have more options and a nicer graphical presentation of the data.

Listing 5.1: Box Plot of `Body Mass on Species

mypenguins |> 
  ggplot(aes(species, body_mass_g)) +
  geom_boxplot()

Note

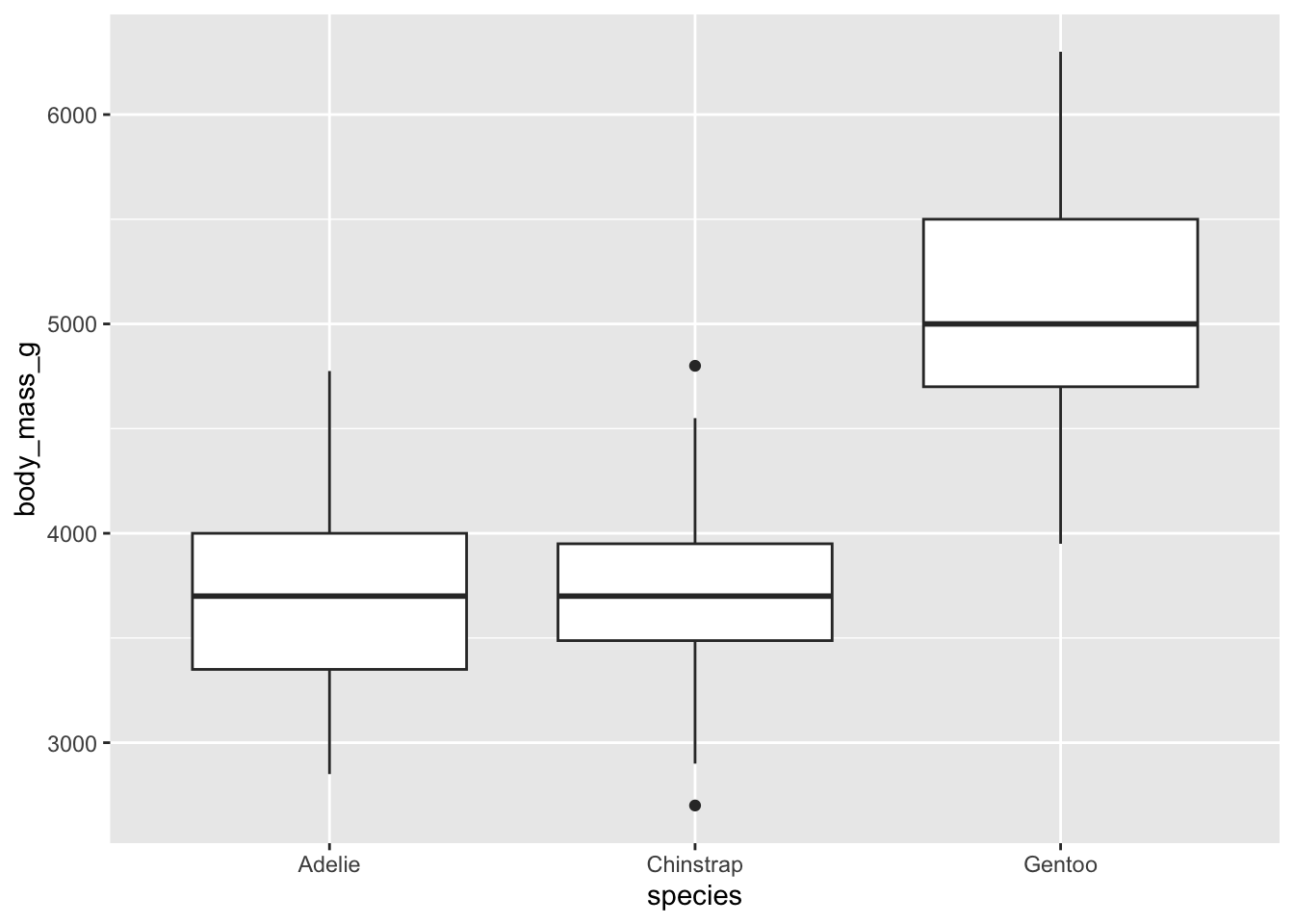
Box plots provide a clear summary of a dataset’s distribution. From a box plot, we can observe:

• The median (central line inside the box),
• The first (Q1) and third (Q3) quartiles (the edges of the box),
• The whiskers, which extend to the smallest and largest values within 1.5 times the interquartile range (IQR = Q3 − Q1),
• Outliers, values beyond the whiskers, are plotted individually as points.

This visualization gives us a good sense of:

• Central tendency (via the median),
• Spread/variability (via the IQR and whiskers),
• Skewness (by checking if the box is symmetric or lopsided),
• And even kurtosis, if there are more outliers than expected, it may suggest heavier tails.

We can make a simpler plot of just the median, min and max if that is of interest.

mypenguins |>
  ggplot(aes(x = species, y = body_mass_g)) +
  stat_summary()

However, these whisker don’t really extend very far. The default length is probably not what you had in mind. We can override these settings like this:

mypenguins |>
  ggplot() +
  stat_summary(
    mapping = aes(x = species, y = body_mass_g),
    fun.min = "min",
    fun.max = "max",
    fun = "median"
  )

We should see some differences in these bars. One question you ought to be asking is whether or not the differences you are seeing are statistically meaningful. We have a test for this.

It’s either a t-test (if you just have two groups) or ANOVA (for 2 or more groups).

We’ve already used a t-test today. Let’s use ANOVA (ANalysis Of VAriance) this time, because we have three groups.

Listing 5.2: Analysis of Variance of `Body Mass on Species

aov_result <- aov(body_mass_g ~ species, data = mypenguins)
summary(aov_result)

             Df    Sum Sq  Mean Sq F value Pr(>F)    
species       2 146864214 73432107   343.6 <2e-16 ***
Residuals   339  72443483   213698                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
2 observations deleted due to missingness

The results of the ANOVA should tell us whether the differences we see are meaningful.

• If the p-value is less than 0.05, we can say the differences are significant at a 95% confidence level.
• Here the \(p\)-value is essentially 0 so we would almost never get this F-Value (343.6) if the Null hypothesis, all groups have equal means, were true.

Note

The F-test in ANOVA checks whether the means of multiple groups are equal.

• Null Hypothesis (\(H_0\)): All group means are equal (no difference).
• Alternative Hypothesis (\(H_1\)): At least one group mean is different.

The F-statistic is the ratio of:

\[F = \frac{\text{Variance between groups}}{\text{Variance within groups}} \tag{5.1}\]

If the between-group variance is much larger than within-group variance, the F-value is high, suggesting a significant difference.

The distribution of the F-statistic is not symmetrical and depends upon two parameters, the degrees of freedom for the numerator in Equation 5.1 and the degrees of freedom for the denominator in Equation 5.1.

We can see the df in the results from Listing 5.2 and extract these two values from the aov summary object. Then we can plot.

summary_result <- summary(aov_result)

# Extract degrees of freedom
df1 <- summary_result[[1]][["Df"]][1]  # Between groups
df2 <- summary_result[[1]][["Df"]][2]  # Within groups

# Create data frame for F-distribution
# Observed F-value
observed_f <- 343.6

# Critical F-value at alpha = 0.05
critical_value <- qf(0.95, df1, df2)

# Generate F-distribution data
f_data <- tibble(x = seq(0, max(6, observed_f + 1), length.out = 1000)) %>%
  mutate(density = df(x, df1, df2))

# Plot
ggplot(f_data, aes(x = x, y = density)) +
  geom_line(color = "steelblue", size = 1) +
  geom_vline(xintercept = critical_value, color = "red", linetype = "dashed") +
  geom_vline(xintercept = observed_f, color = "darkgreen", linetype = "dotted") +
  annotate("text", x = critical_value + 0.5, y = max(f_data$density) * 0.9,
           label = "Critical value (α = 0.05)", color = "red", hjust = 0) +
  annotate("text", x = observed_f - 5, y = max(f_data$density) * 0.5,
           label = paste("Observed F =", observed_f), color = "darkgreen", hjust = 1) +
  labs(
    title = paste("F-distribution (df1 =", df1, ", df2 =", df2, ")"),
    x = "F value (log scale)", y = "Density"
  ) +
  theme_minimal() + 
  scale_x_log10()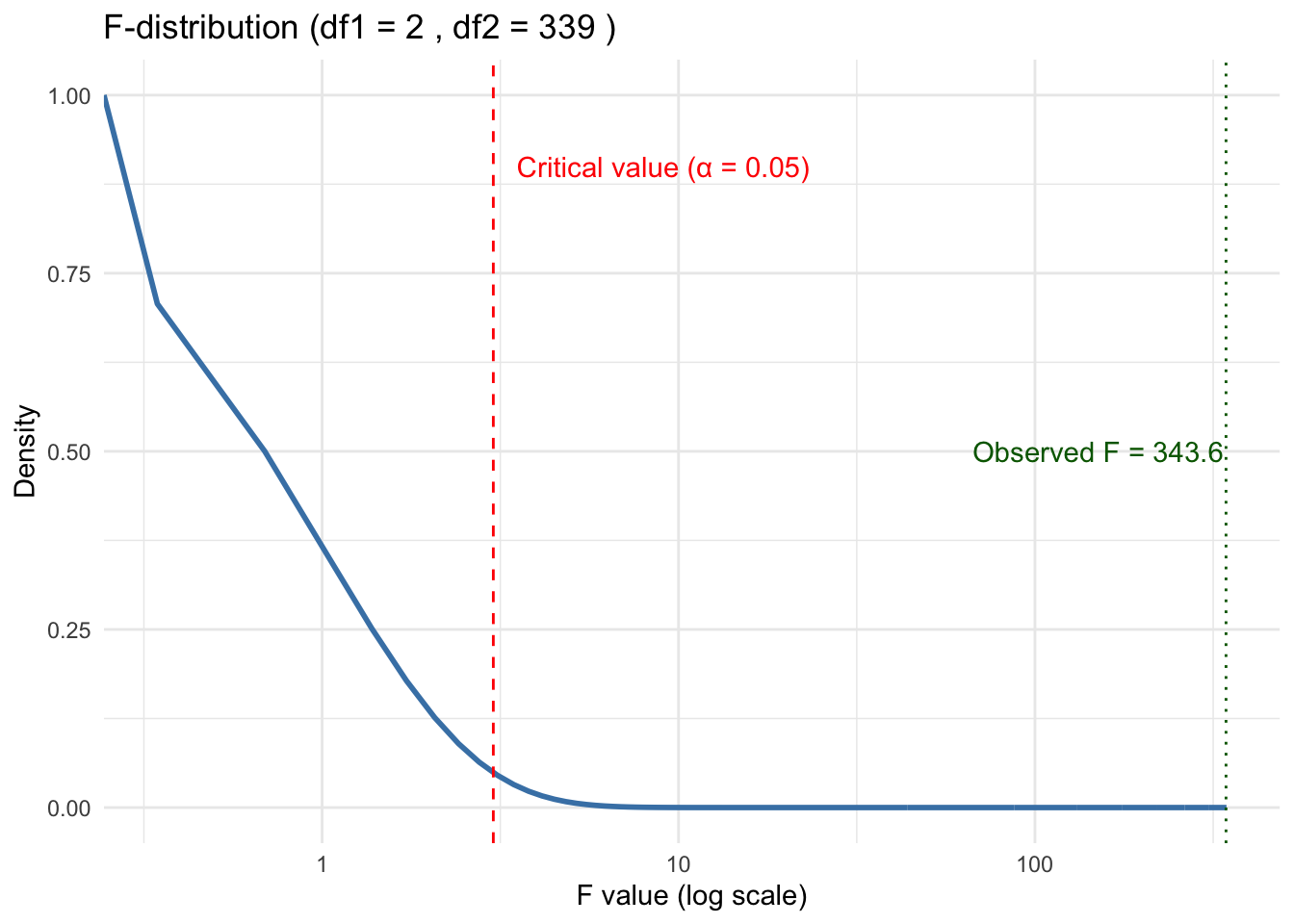

If this happens, we then can move on to Tukey (or Bonferroni) to sort out which groups are actually different from each other.

• It’s pretty clear from the box plot Listing 5.1 which one of these things is not like the other.
• However, we can do another statistical test, Tukey’s HSD (Honestly Significant Difference) test to confirm.
• This is a post-hoc test, performed after, a statistically significant ANOVA result (say, \(p\) < 0.05).
• It compares all pairs of group means and tells you which pairs differ significantly.

TukeyHSD(aov_result) # If there is a difference, which groups differ?

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = body_mass_g ~ species, data = mypenguins)

$species
                       diff       lwr       upr     p adj
Chinstrap-Adelie   32.42598 -126.5002  191.3522 0.8806666
Gentoo-Adelie    1375.35401 1243.1786 1507.5294 0.0000000
Gentoo-Chinstrap 1342.92802 1178.4810 1507.3750 0.0000000

• These results show no difference between Chinstrap and Adelie and a highly significant difference, \(p\)-value of 0, between Gentoo and the other two species.

5.6 Linear Regression Tests

Let’s revisit the plot of university and general_revenue_per_person to see if there is a relationship between them and if we can use university to “predict” the general_revenue_per_person.

house_ed_gdp_joined <- read_csv("data/house_ed_gdp_joined.csv")
mywk <- house_ed_gdp_joined |>
  mutate(largeFam = Average_size > 3.5)

mywk |>
  ggplot(aes(x = university, y = general_revenue_per_person)) +
  geom_point() +
  geom_smooth(se = FALSE)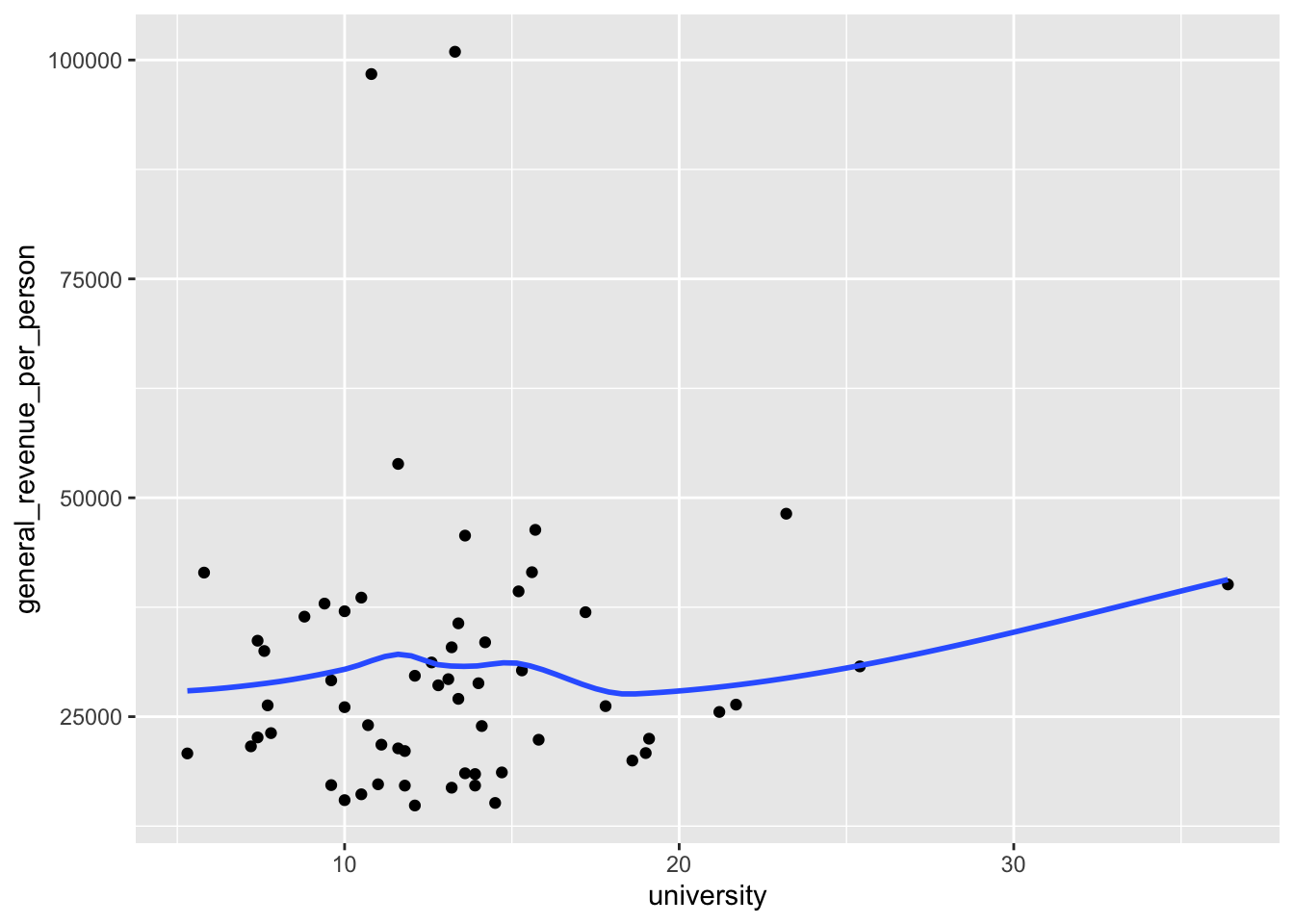

If we convert the smoother to a linear smoother, we see the straight line for a regression model.

mywk |>
  ggplot(aes(x = university, y = general_revenue_per_person)) +
  geom_point() +
  geom_smooth(method = lm, se = FALSE)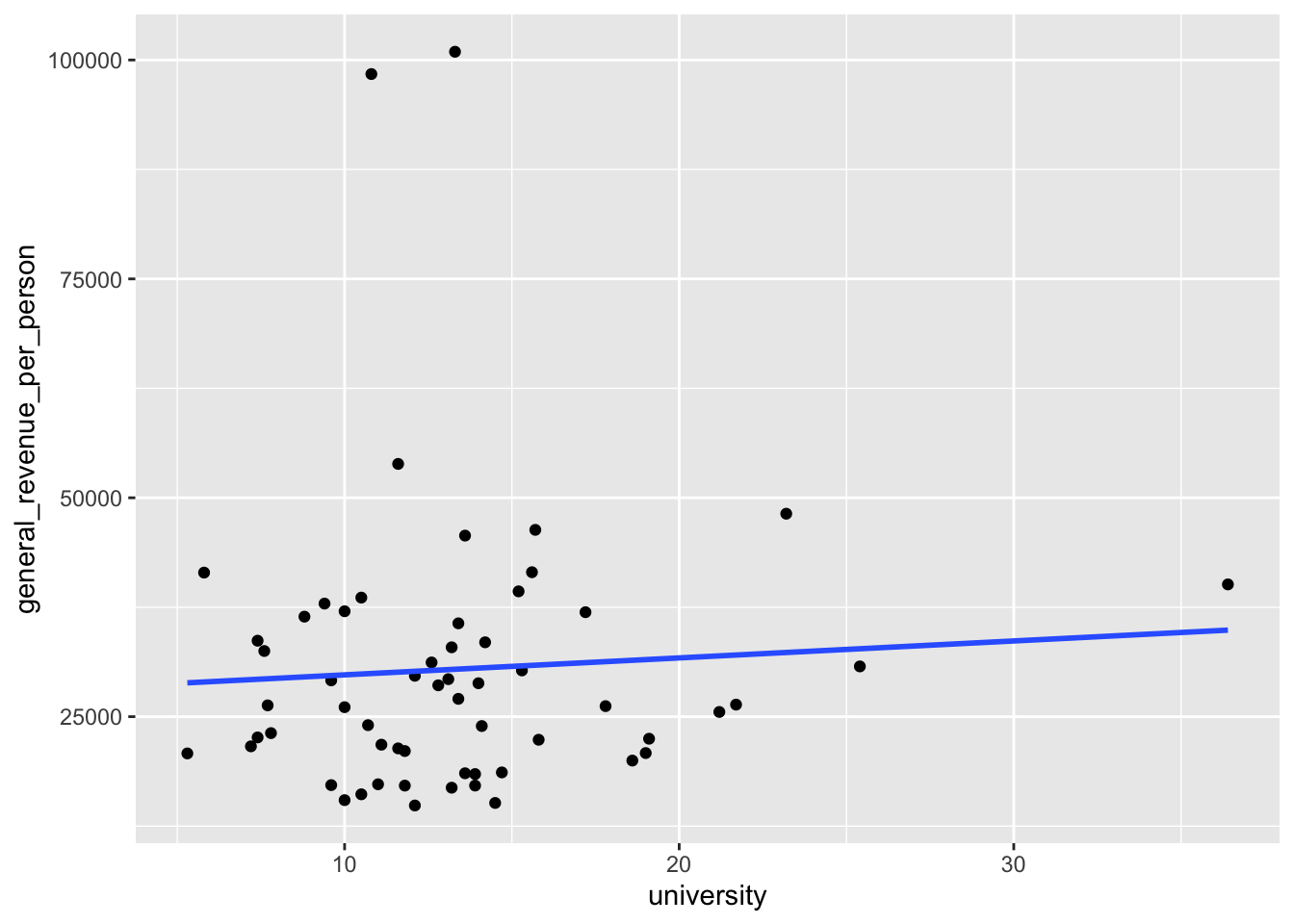

Figure 5.1: A scatterplot of two variables with the linear smoother

• This regression line suggests there could be a positive relationship between the two variables. But is it real?

Let’s run a test!

• Use the lm() function to create a linear regression model.
• We will use the ~ tilde operator (it’s the squiggly line, not a minus sign) to separate the two sides of our model “formula”.
  • The left side is the response we are trying to predict and the right side is all of our predictor variables.

my_model <- lm(general_revenue_per_person ~ university, data = mywk)
class(my_model)

[1] "lm"

The resulting object has class lm which means is is a linear regression model object.

• It has lots of information about the model.

Show the object and we get the basic results.

my_model

Call:
lm(formula = general_revenue_per_person ~ university, data = mywk)

Coefficients:
(Intercept)   university  
    27840.0        193.6  

• The coefficients here are the two parameters of the line we saw in Figure 5.1.
  • This is known as the “fitted line” and all the predictions are points on this line.
  • The intercept is where it crosses the y axis and the university coefficient is the slope of the line.
  • We interpret that coefficient as saying for every 1 percent increase in university, the general_revenue_per_person can be expected to increase by 193.6.

5.6.1 Interpreting the Summary Information on the Coefficients

We can use summary() to get much more information about the model.

• Note that the summary() function is a generic function that calls special methods for different class objects. Since our model is class lm, the actual function being called is summary.lm() which is what you look for in the help.

summary(my_model)

Call:
lm(formula = general_revenue_per_person ~ university, data = mywk)

Residuals:
   Min     1Q Median     3Q    Max 
-15501  -9052  -3398   5224  70528 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  27840.0     5883.7   4.732 1.51e-05 ***
university     193.6      411.5   0.470     0.64    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 16150 on 57 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared:  0.003867,  Adjusted R-squared:  -0.01361 
F-statistic: 0.2213 on 1 and 57 DF,  p-value: 0.6399

The summary tells us several items of interest.

1. The formula used to build the model.
2. The Residuals statistics about the differences between the observed response values and the predicted values (i.e., the residuals).
3. Coefficient estimates, along with additional diagnostic statistics:

• Std. Error: The standard error of the estimate — a measure of how much the estimate would vary if you repeated the experiment.
• t value: The t-statistic, calculated by dividing the estimate by its standard error.
• Pr(>|t|): The probability of observing a t-value as extreme as the one calculated, assuming the Null Hypothesis is true. Smaller values indicate stronger evidence against the Null Hypothesis.
  • For example, a value of 0.05 means there’s a 5% chance of observing such a result under the Null — considered rare enough to reject it.
  • A large value like 0.66 suggests the result is common under the Null, providing little reason to reject it.
• Signif. codes: A legend showing how significant a result is using , , or .

Important

What is this Null Hypothesis and why does it matter?

The Null Hypothesis is a statement about the “true” value of a coefficient — in linear regression, it’s typically assumed to be 0. Why?

• If the true value is 0, we can use known statistical distributions to compute the probability of observing a non-zero estimate.
• A statistic that is considered unlikely under the Null is called significant.

In practice, the Null Hypothesis is sometimes jokingly called the “Dull Hypothesis”, because it’s asserting that nothing interesting is happening, i.e., there’s no relationship between the predictor and response variable.

So we now know enough to determine if any of coefficients are significant.

• The intercept has a \(p\)-value that is close to zero so it is rare. That means we can reject the null hypothesis that the intercept = 0.
• The variable university has a \(p\)-value of .64. That is quite high so this variable is Not significant. There is almost no evidence of a relationship between the two variables.

The top part of the summary() output focuses on the individual coefficients. Each variable in the model formula gets a line of output, which lets us determine which variables are statistically significant and which are not.

5.6.2 Interpreting the Summary Information on the Overall Model

Now, let’s look at the bottom portion of the output. This contains information about the overall model:

1. Residual standard error: 16150 on 57 degrees of freedom

• This tells us the standard deviation of the residuals (i.e., the errors between predicted and actual values).
• While the number itself isn’t very informative in isolation, it becomes useful when comparing models.
• The degrees of freedom (df) are more interesting. We had 61 total observations, but 2 were deleted due to missing values. Of the remaining 59, 2 were used for the model (one for the intercept, one for the predictor university). So: \(61 - 2_{\text{missing}} - 2_{\text{model}} = 57 \text{df}\)

2. (2 observations deleted due to missingness) A note explaining why there’s a drop in degrees of freedom.

3. Multiple R-squared: 0.003867, Adjusted R-squared: -0.01361

• The Multiple R-squared measures how much variation in the response variable is explained by the model. A value like 0.90 would be considered strong, but here the value is very low, suggesting the model explains almost none of the variation in the data.
• The Adjusted R-squared adjusts the multiple R-squared based on the number of predictors in the model. This helps prevent overfitting by penalizing the addition of unnecessary variables. If we kept adding variables, \(R^2\) might increase even if those variables are meaningless so using adjusted \(R^2\) helps counteract that.

4. F-statistic: 0.2213 on 1 and 57 DF, p-value: 0.6399

• The F-statistic tests whether the entire model is statistically significant. The Null Hypothesis here is that all coefficients (except the intercept) are zero, in other words, none of the predictors have an effect.
• A small \(p\)-value would give us evidence to reject this Null Hypothesis. But here, the \(p\)-value is 0.6399, which is not rare. We have “insufficient evidence” to conclude that the model explains a meaningful portion of the variation in the response.
  • Note that since we only had one variable in the model the F-statistic \(p\)-value is the same as the t-statistic \(p\)-value.

So, our tests tell us that despite the slightly positive slope in Figure 5.1, there is no real relationship. That line is just the result of forcing a line on random variation.

5.6.3 Residual Plots

We won’t discuss these now, but the base R plot function has a special method, plot.lm() for doing quick plots for a liner regression model.

• These plots are designed to help you interpret how well the model fits the data and the statistical assumptions about the data that support generating the \(p\)-values.

plot(my_model)

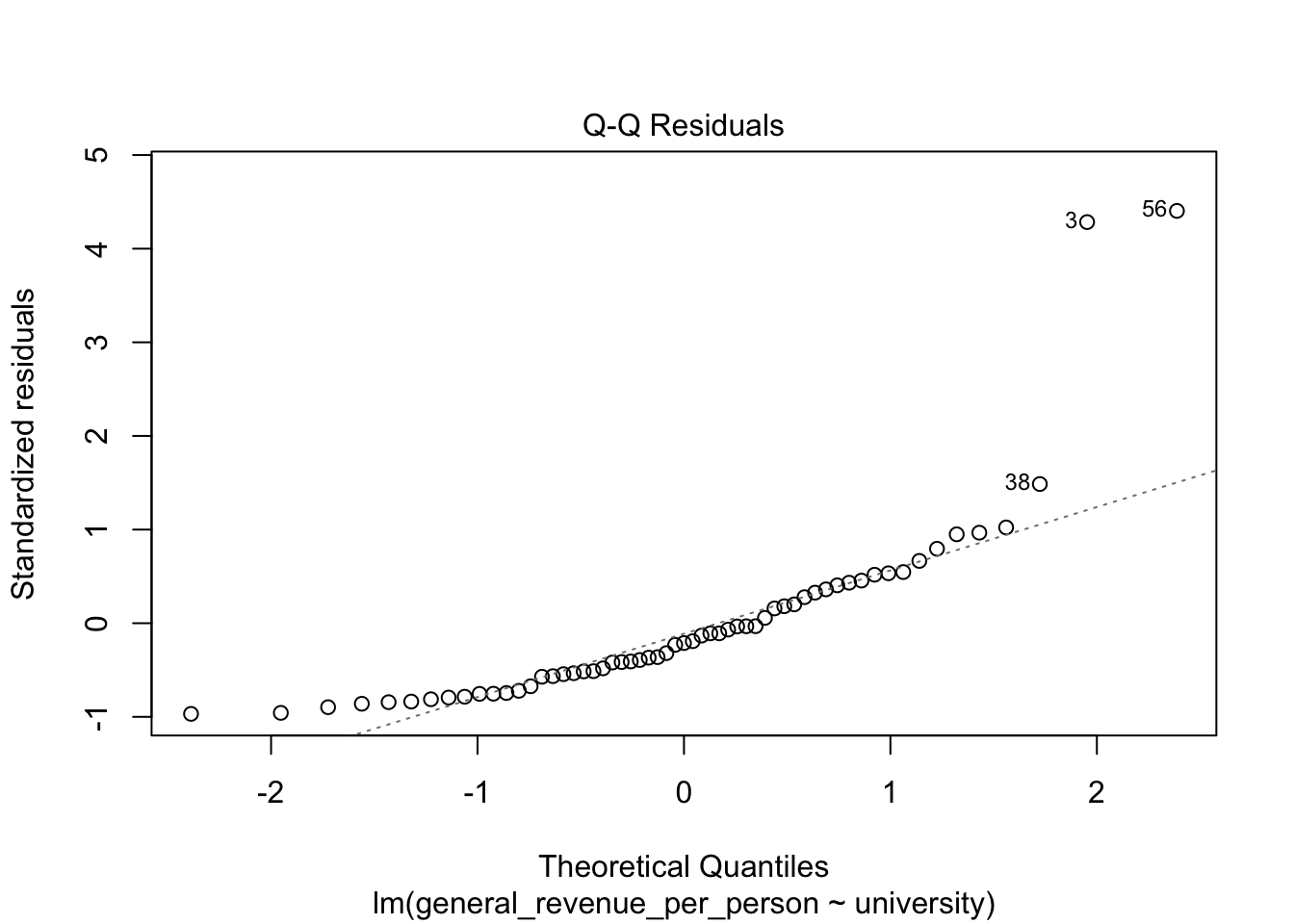
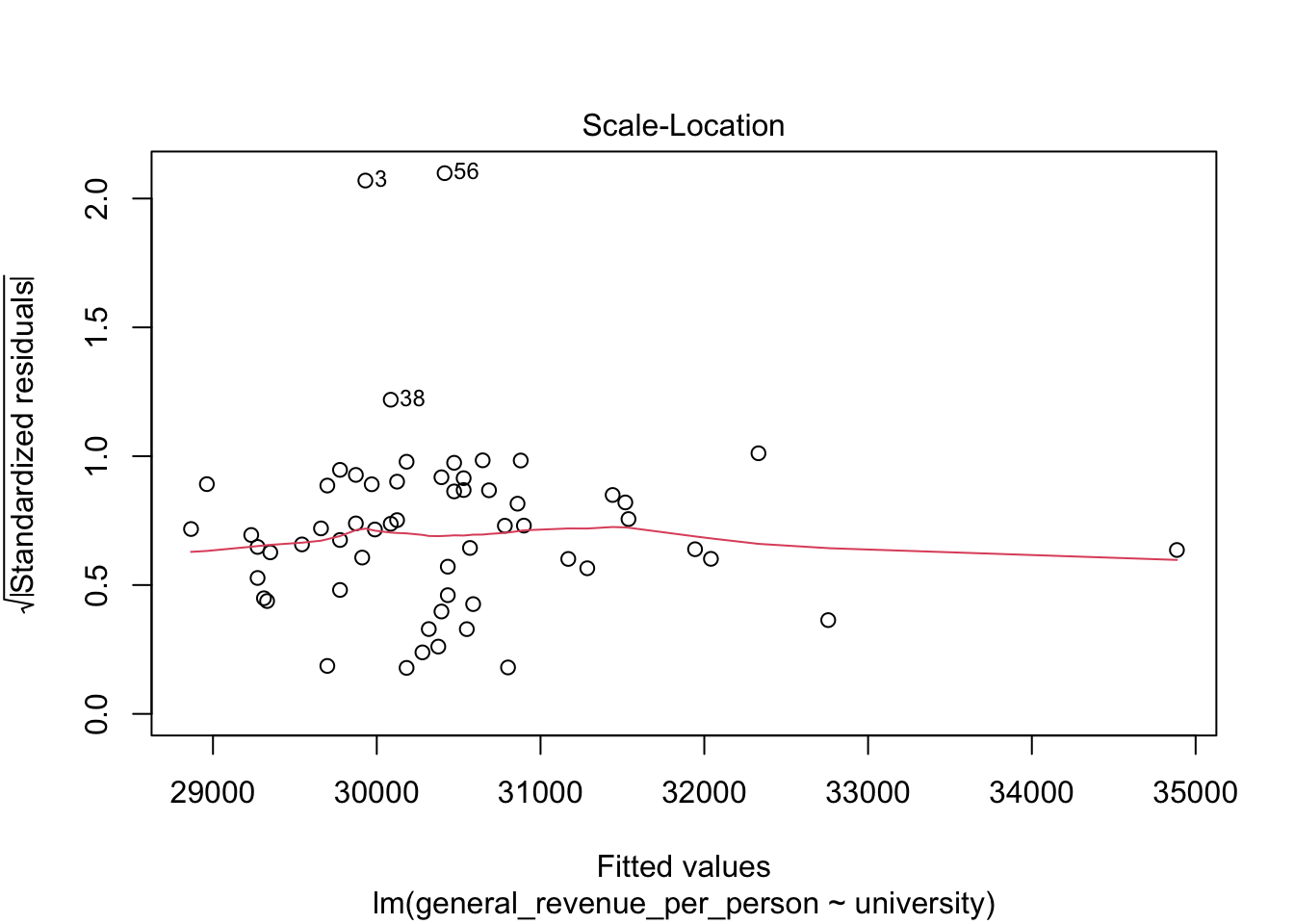
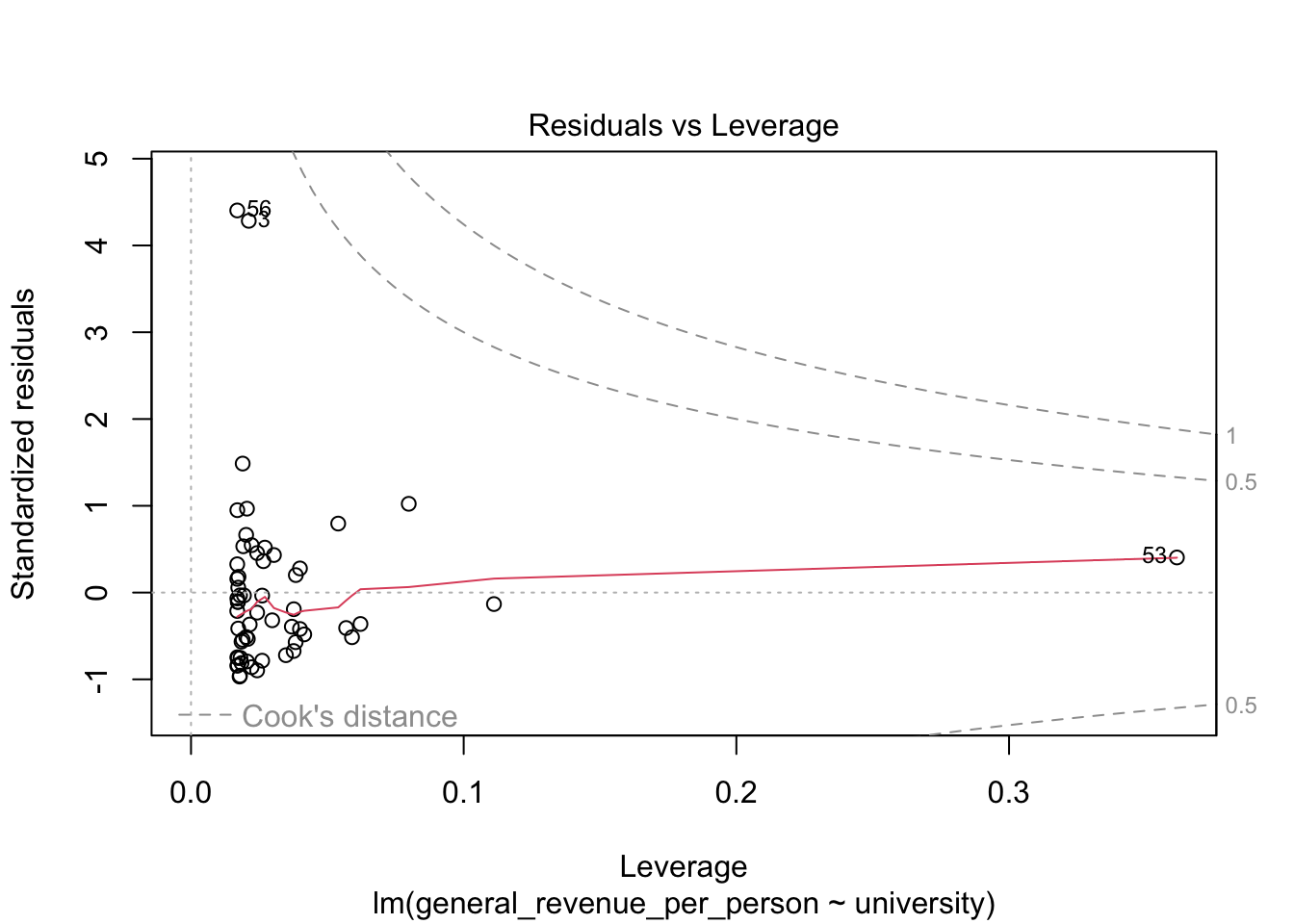
5.6.4 Multivariate Regression Tests

It can be a challenge to plot additional variables in 3, 4, 5 dimensions but it is easy to add them to the model.

Let’s add has_computer and population to see if they help.

my_model2 <- lm(general_revenue_per_person ~ university + has_computer +
  population, data = mywk)
summary(my_model2)

Call:
lm(formula = general_revenue_per_person ~ university + has_computer + 
    population, data = mywk)

Residuals:
   Min     1Q Median     3Q    Max 
-17641  -9919  -3166   5366  67713 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.702e+04  7.360e+03   3.671 0.000548 ***
university    1.051e+03  6.709e+02   1.567 0.122904    
has_computer -5.718e+02  4.702e+02  -1.216 0.229107    
population   -1.949e-02  3.915e-02  -0.498 0.620585    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 16070 on 55 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared:  0.04914,   Adjusted R-squared:  -0.002723 
F-statistic: 0.9475 on 3 and 55 DF,  p-value: 0.4241

The summary now shows multiple lines with the additional variables. Unfortunately, the \(p\)-values are all large.

While the Multiple R-squared has increased, the Adjusted R-squared is actually negative which means adding these variables does nothing to improve the model.

So begins the quest of the data scientist to see if they can find variables to explain a quantity of interest!

5.7 Exercise

You can continue with the data from the previous two lessons.

1. Subsetting

Demonstrate how to create at least two subsets from your main data, by splitting according to either a Boolean condition, or by a categorical variable. (You are not required to recode a variable.)

2. Demonstrate a t-test using two subsets you created.

3. Draw a linear (or smooth) fit

Choose two numerical variables for this. Maybe a linear is not a great choice. Why or why not?

4. Demonstrate the use of a Chi-Square test based on two of the categorical variables in your data.

You might be inspired by your previous bar plots.

5. Try an ANOVA test!

You might be inspired by your previous box plot.

ASA, American Statistical Association. 1983. “Auto Data Set from the 1983 Exposition of Statistical Graphics Technology.” https://lib.stat.cmu.edu/data-expo/1983.html.

Barret, Tyson, Matt Dowle, Arun Srinivasan, Jan Goreck, Michael Chirico, Toby Hocking, Benjamin Schewndinger, and Ivan Krylob. 2025. “Data.table: Extension of ‘Data.frame‘.” https://r-datatable.com.

Bartley, Kevin. 2024. “Data Statistics (2025) - How Much Data Is There in the World?” Rivery. https://rivery.io/blog/big-data-statistics-how-much-data-is-there-in-the-world/.

Davenport, Thomas H., and D J. Patil. 2012. “Data Scientist: The Sexiest Job of the 21st Century.” Harvard Business Review October 2012: 70–76. http://hbr.org/2012/10/data-scientist-the-sexiest-job-of-the-21st-century/ar/1.

Firke, Sam. 2024. “Janitor: Simple Tools for Examining and Cleaning Dirty Data.” https://sfirke.github.io/janitor/.

Fox, John, and Sanford Weisberg. 2019. An {}R{} Companion to Applied Regression. Third. Sage. https://www.john-fox.ca/Companion/.

Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2010. “Regularization Paths for Generalized Linear Models via Coordinate Descent{}.” Journal of Statistical Software 33 (1): 1–22. https://doi.org/10.18637/jss.v033.i01.

Godsey, Brian. 2017. Think Like a Data Scientist. Manning.

Grolemund, Garrett, and Hadley Wickham. 2011. “Lubridate: Dates and Times Made Easy with {Lubridate}.” Journal of Statistical Software 40 (3): 1–25. https://www.jstatsoft.org/v40/i03/.

———. n.d. R for Data Science. https://r4ds.had.co.nz/.

Horst, Allison, Alison Presmanes Hill, and Kristen B Gorman. 2020. “Palmerpenguins R Data Package.” https://doi.org/10.5281/zenodo.3960218.

Ian Fellows. 2022. “Wordcloud: Word Clouds.” Comprehensive R Archive Network. https://doi.org/10.32614/CRAN.package.wordcloud.

Institute of Statistics (INSTAT). 2025. “Statistical Database.” https://databaza.instat.gov.al:8083/pxweb/en/DST/.

Institute, QLB Brain. 2017. “Stunning Neuroscience Images.” https://qbi.uq.edu.au/blog/2017/07/stunning-neuroscience-images.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2023. An Introduction to Statistical Learning with Applications in R. 2nd ed. Springer. https://www.statlearning.com.

Kalinowski, Tomasz et al. 2022. “TensorFlow for R.” https://tensorflow.rstudio.com/.

Kalinowski, Tomasz, JJ Allaire, and François Chollet. 2025. “Keras3: R Interface to Keras.” https://keras3.posit.co/.

Kanwal, Maxinder S., Avinash S. Ramesh, and Lauren A. Huang. 2013. “A Novel Pseudoderivative-Based Mutation Operator for Real-Coded Adaptive Genetic Algorithms.” F1000Research. https://doi.org/10.12688/f1000research.2-139.v2.

Kaplan, Daniel, and Randall Pruim. 2023. “Ggformula: Formula Interface to the Grammar of Graphics.” https://www.mosaic-web.org/ggformula/.

Karatzoglou, Alexandros, Alex Smola, Kurt Hornik, National ICT Australia (NICTA), Michael A. Maniscalco, and Choon Hui Teo. 2024. “Kernlab: Kernel-Based Machine Learning Lab.” https://CRAN.R-project.org/package=kernlab.

Kelechava, Brad. 2018. “The SQL Standard - ISO/IEC 9075:2023 (ANSI X3.135).” The ANSI Blog. https://blog.ansi.org/sql-standard-iso-iec-9075-2023-ansi-x3-135/.

Khun, Max, and Julia Silge. 2023. Tidy Modeling with R. https://www.tmwr.org/.

Lin, Hause, and Tawab Safi. 2025. “Ollamar: An R Package for Running Large Language Models.” Journal of Open Source Software. https://doi.org/10.21105/joss.07211.

Myer, David. 2024. “E1071: Misc Functions of the Department of Statistics, Probability Theory Group.” https://cran.r-project.org/web/packages/e1071.

Neuroscientifically Challenged. 2014. “2-Minute Neuroscience: The Neuron.” https://www.youtube.com/watch?v=6qS83wD29PY.

Nohe, Patrick. 2017. “What Is the Dark Web?” https://www.thesslstore.com/blog/what-is-the-dark-web/.

“Ollama.” 2025. https://ollama.com.

“Open Data Inventory—Global Index of Open Data - Open Data Inventory.” n.d. Accessed May 8, 2025. https://odin.opendatawatch.com/.

Posit. 2025a. “Posit Cheatsheets.” https://posit.co/resources/cheatsheets/.

———. 2025b. “RStudio IDE User Guide.” RStudio User Guide. https://docs.posit.co/ide/user/.

“Quarto.” 2025. Posit.co. https://quarto.org/.

Rashida048. 2020. “Machine Learning: Gradient Descent Concept – Regenerative.” https://regenerativetoday.com/machine-learning-gradient-descent-concept/.

Robinson, Julia Silge and David. n.d. Text Mining with R. Accessed April 12, 2020. https://www.tidytextmining.com/.

Ruman. 2023. “Convex Vs. Non-Convex Functions: Why It Matters in Optimization for Machine Learning.” Medium. https://rumn.medium.com/convex-vs-non-convex-functions-why-it-matters-in-optimization-for-machine-learning-39cd9427dfcc.

Silge, Julia, and David Robinson. 2022. Tidytext: Text Mining with R. O’Reilly Media, Inc. https://www.tidytextmining.com/.

———. 2023. “Tidytext: Text Mining Using Tidy Tools.” https://juliasilge.github.io/tidytext/.

Sjoberg, Daniel D., Karissa Whiting, Michael Curry, Jessica A. Lavery, and Joseph Lamarange. 2021. “Reproducible Summary Tables with the Gtsummary Package.” The R Journal 13 (1): 570–80. https://doi.org/10.32614/RJ-2021-053.

Team, R Core. 2018. “R: A Language and Environment for Statistical Computing.” R Foundation for Statistical Computing. https://www.R-project.org/.

Ushey, Kevin, JJ Allaire, and Yuan Tang. 2023. “Reticulate: R Interface to Python.” https://rstudio.github.io/reticulate/.

van Rossum, Guido. 2025. “Python.” https://www.python.org/.

Waring, Elin, Michael Quinn, Amelia McNamara, Eduardo Arino d la RUbia, Shu Hao, and Shannon Ellis. 2025. “Skimr: Compact and Flexible Summaries of Data.” https://docs.ropensci.org/skimr/.

Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org/.

———. 2023a. “Forcats: Tools for Working with Categorical Variables (Factors).” https://forcats.tidyverse.org/.

———. 2023b. “Modelr: Modelling Functions That Work with the Pipe.” https://modelr.tidyverse.org/.

———. 2023c. “Stringr: Simple, Consistent Wrappers for Common String Operations.” https://stringr.tidyverse.org/.

Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain Francois, Garret Grolemund, et al. 2019. “Welcome to the {Tidyverse}.” Journal of Open Source Software, no. 43: 1686. https://doi.org/10.21105/joss.01686.

Wickham, Hadley, Mine Cetinkaya-Rundel, and Garrett Grolemund. 2023. R for Data Science (2e). O’Reilly Media, Inc. https://r4ds.hadley.nz/.

Wickham, Hadley, Romain Francois, Lionel Henry, Kirill Muller, and Davis Vaughan. 2023. “Dplyr: A Grammar of Data Manipulation.” https://dplyr.tidyverse.org.

Wickham, Hadley, Jim Hester, and Jennifer Bryan. 2024. “Readr: Read Rectangular Text Data.” https://readr.tidyverse.org/.

Wickham, Hadley, Davis Vaughan, and Maximilian Girlich. 2023. “Tidyr: Tidy Messy Data.” https://tidyr.tidyverse.org.

Wikipedia. 2025. “Data Science.” Wikipedia. https://en.wikipedia.org/wiki/Data_science.